가공 스테이지와 반사경 이동 량을 결정하는 임계값이 LASER 가공오차에 미치는 영향에 관한 연구

2.1 시스템 구조

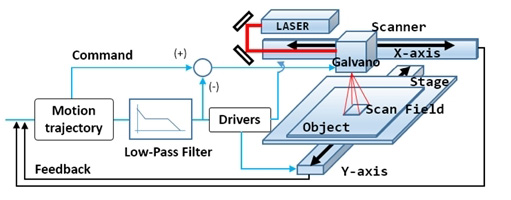
MOTF 레이저 가공 공정을 구현하기 위하여 스캐너를 구동하는 x축과 스테이지를 구동하는 y축의 hybrid 시스템을 Fig. 1과 같이 구성하였다^[6]. 시스템의 x, y축은 하나의 제어기를 통해서 제어할 수 있도록 kinematics를 묶어서 하나의 좌표계를 통한 벡터 이송이 가능하도록 하였다. 이를 위하여 가공좌표를 G 코드로 변환하였으며, 복잡한 가공경로로 인하여 스테이지 이송경로를 산출하는데 발생하는 이산분포를 motion controller가 사전에 최적화된 경로로 변환하여 이산분포를 좁힐 수 있도록 한다.

Fig. 1

LASER scanner & hybrid Stage

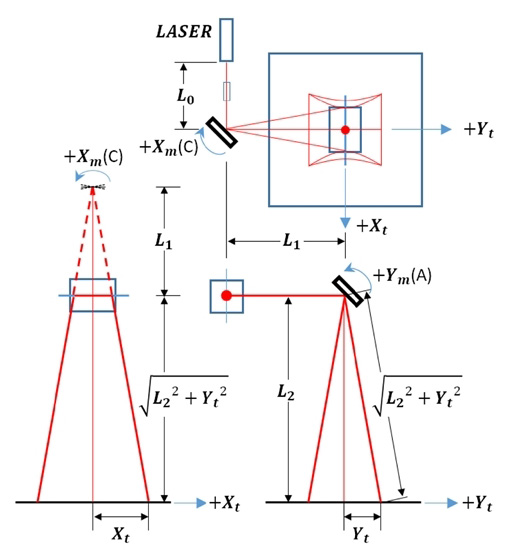
Fig. 2는 스캐너와 스테이지의 x, y축 이송을 하나의 좌표계로 묶어서 제어하기 위한 kinematics를 도식화 한 것이며, 스캐너의 갈바노미러에 반사되는 레이저 빔의 궤적을 수식으로 설명하고 있다. L₀는 레이저와 첫 번째 갈바노미러 사이의 거리이며, (A)와 (C)는 각 갈바노미러의 회전량을 의미한다. L₁은 미러 간의 중심거리를 나타내고, L₂는 스캐너와 가공 면 사이의 거리를 나타낸다.

Fig. 2

Scanner kinematics[6]

이를 수식으로 표현하면 식 (1)과 (2)와 같다^[7]. 스캐너를 구성하는 미러의 회전운동에 따른 중심선의 궤적을 평면 좌표계 상에 투영한 것이다.

스캐너에 입사되는 레이저는 미러의 회전 각도인 +X_m(C), +Y_m(A)에 따라 (X_t, X_y) 좌표에 입사된다. 이 식들은 모터의 제어신호를 기준으로 절대좌표계의 x, y축 위치를 나타내는 forward kinematics 수식으로 사용된다. 식 (3)과 (4)는 보간 연산에 의해 생성된 궤적마다의 절대 위치 값을 모터 지령 값으로 변환하는 inverse kinematics를 수식화 한 것이다^[6].

2.2 저역필터(Low-pass filter)

MOTF 공정에서 가공 오차를 줄이기 위하여 저역필터를 사용하였으며, 필터의 cut-off 값에 따라 스테이지와 스캐너의 제어신호 비중을 조절하였다. 또한 반응성을 조절하는 Q-gain값을 조절하여 가공 정밀도에 미치는 영향을 분석하였다.

식 (5)는 스테이지와 스캐너가 하나의 좌표계상에서 갖는 위치를 설명하고 있다^[6].

X_Hpf는 고주파 성분의 제어신호로 표현하는 스캐너의 위치이며, X_Lpf는 저주파 성분의 제어신호로 표현하는 스테이지의 위치이다. X_Hpf는 식 (1)에서 (2)의 스캐너의 kinematics에서 정의하였으며, X_Lpf는 다음의 식 (6)에서 설명하고 있다^[6].

이는 50 mm 크기의 스캔 영역을 가지고 고속 회전 하는 갈바노미러의 제어신호와 가공좌표의 근사위치로 저속 이동하는 스테이지의 제어신호를 분리하기 위한 저역필터를 적용한 식이다. 여기서 X_{kin back}(1)과 (2)는 각각 kinematics에서 피드백 에러이며, X_{Lpf back}(1)과 (2)는 저역필터 신호에 따른 kinematics position이다. 또한 K_a0~2는 kinematics position을 위한 gain 값이며, K_b0~2는 저역필터링 된 kinematics position을 위한 gain 값이다. 특히 K_a0은 저주파 성분의 스테이지의 위치 제어신호 값을 산출하는데 결정적인 역할을 한다. 다음의 식 (7)~(9)는 저역필터를 수식으로 표현한 것이다^[6].

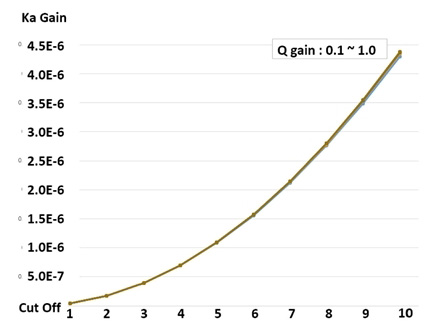
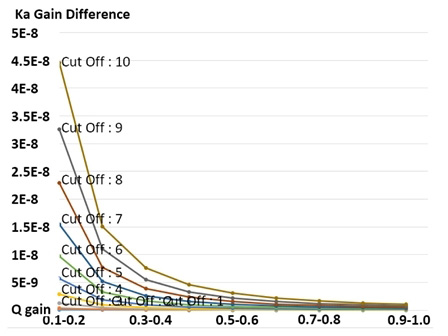
식 (7)에서 T_s는 보간이 생성된 위치에 대한 제어신호 실행주기이다. F_c는 스테이지의 제어신호 비율을 결정하는 cut-off 값을 의미한다. 신호 입력에 따라 K_g가 0~∞의 범위를 가질 수 있으나 T_s가 수 msec 임을 감안한다면 0에 수렴하게 된다. K_g에 영향을 받는 식 (8)~(9)에서 볼 수 있듯이 분자가 분모에 비해 매우 작기 때문에 저역필터가 적용된 스테이지 이송 명령이 나머지 스캐너 이송 명령에 비해 매우 작음을 알 수 있다. 이에 따라 저역필터는 스테이지 이송을 미소량으로 제한하고 스캐너의 이송량을 늘리는 방식을 적용하였다. 보간 데이터 생성 주기인 T_s를 15 msec로 고정하였을 때 저역필터 제어신호를 실질적으로 결정하는 K_a0를 임계값인 F_c와 Q-gain 값인 Q_g의 상관관계를 도표화 하면 Fig. 3과 4와 같다. Fig. 3에서와 같이 cut-off 값이 변화함에 따라 비선형적인 증가하는 경향을 보인다. 그러나 저역필터 cut-off 값에 따른 변화의 정도가 매우 작기 때문에 추가로 gain 값을 조절하였다. 이는 동일하게 스테이지의 구동 비중을 조절하는 역할을 하며, 스테이지의 가속도 설계 값을 고려하여 설정하였다. Fig. 4는 Q-gain 조절에 따른 반응성 변화 그래프로 표현한 것이다. 결과적으로 가공 스테이지의 제어신호 비율을 cut-off 값과 Q-gain 값을 통하여 조절하여 가공 정밀도가 개선되는 것을 실험적으로 분석하였다.

Fig. 3

Low-pass filter gain by Cut-Off value

Fig. 4

Low-pass filter gain by Q gain value

3.1 실험장치

본 연구에서는 대 면적 가공을 위하여 레이저 스캐너의 구동 축(x)와 가공 스테이지의 구동 축(y)가 분리된 구조의 hybrid linear 시스템을 Fig. 5와 같이 구성하였으며, 시스템 사양과 시험 조건은 Table 1과 같다. MOTF 가공을 위한 데이터는 지정된 블록단위 크기의 스캔 영역 내의 가장 가까운 데이터부터 정렬하는 greedy알고리즘을 통해서 가공 순서를 재 정렬 하였으며, 스캔 영역 간의 최단 경로 연산을 통해서 전체 경로를 단순화 하였다. 그리고 본격적인 실험에 앞서 구동 중 발생되는 진동 측정을 통해서 고유 진동수에 적합한 방진패드를 부착하였으며, 구동 제어신호에 대해 50 msec 이내에 안정적인 추종이 되도록 tuning하였다.

Fig. 5

Hybrid laser machining stage

Table 1

MOTF equipment specifications & test conditions

3.2 실험방법

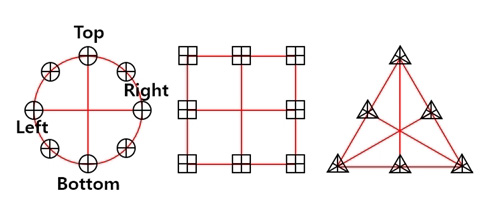
MOTF 가공 방식에 의한 대면적 가공 정밀도를 실험적으로 확인하기 위하여 Fig. 6과 같이 rectangle (1 mm), circle (2 mm), triangle (2 mm) 가공 패턴을 활용하였다. 이는 동일한 형상에 크기가 300 mm 인 대형 패턴을 가공하고, 그 경로 상에 소형 패턴을 가공하여 교차되는 부분의 위치 정밀도를 측정하였다. 측정에는 Olympus STM7 광학현미경을 이용하였으며, 패턴에 따라 다음의 방법으로 확인하였다.

Fig. 6

MOTF machining patterns

• 1. 가공위치 오차 확인
• ∙ Rectangle 중심선 접선 두께와 rectangle line 두께 편차
• ∙ Triangle 무게중심과 교차되는 triangle line 사이의 거리
• ∙ Circle 중심선 접선 두께와 circle line 두께 편차
• 2. 가공모양 확인
• ∙ Circle 진원도

가공스테이지의 구동 제어신호 비중을 조율하는 cut-off 값의 범위를 1~10범위로 하고 1단위로 값을 변화시켜서 가공위치의 정확도를 확인하였다. 이때 Fig. 4에서와 같이 임의의 cut-off 값이 Q-gain의 영향을 받지 않는 안정화 구간에 진입하는 0.7의 값으로 실험하였다. 실험에서 얻어진 cut-off 값을 기준으로 Q-gain 변화에 따른 가공위치의 정확도를 측정하는 방식으로 실험을 진행하였다.

4.1 Cut-Off에 따른 가공 오차

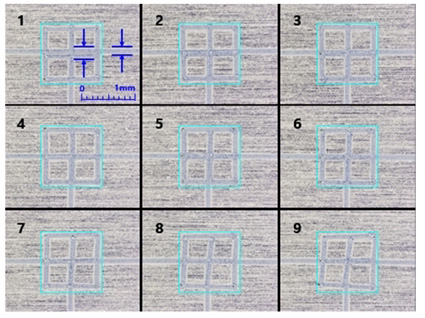
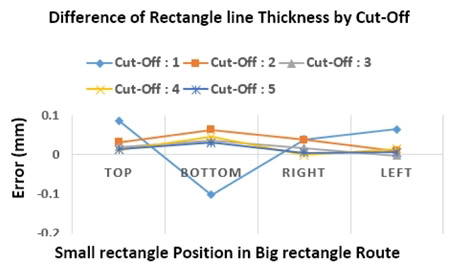
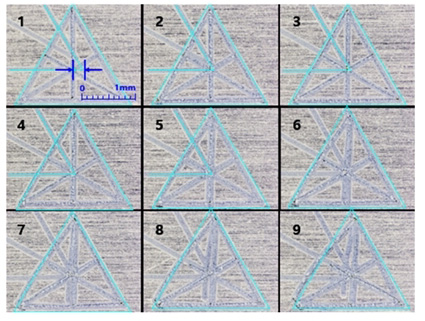
Fig. 7에서와 같이 밑그림으로 먼저 가공된 대형 사각형 경로를 따라서 1 mm 크기의 소형 사각형이 중첩 가공되는 구간 두께와 편차를 통하여 가공오차를 확인하였다. Cut-off 값이 커짐에 따라 가공스테이지의 관성 부하로 인해서 가공오차가 크게 발생함을 확인 할 수 있다. 가공 상태가 매우 불량하여 측정의 의미가 없는 cut-off 값 (6~9)을 배제한 가공 오차는 Fig. 8의 그래프에서 확인할 수 있다.

Fig. 7

Rectangle (Crosshair) line image

Fig. 8

Rectangle (Crosshair) line thickness error

사각형 패턴을 따라서 가공을 할 경우 가공 벡터의 변화가 없거나 모서리 부분에서 제한적으로 발생하므로 cut-off 값이 높아지더라도 가공 모양에 대한 오차가 적음을 알 수 있다. Cut-off 값이 5 일 때 접선 두께에 대한 오차의 평균은 13 μm와 표준편차는 11 μm로 측정되었다.

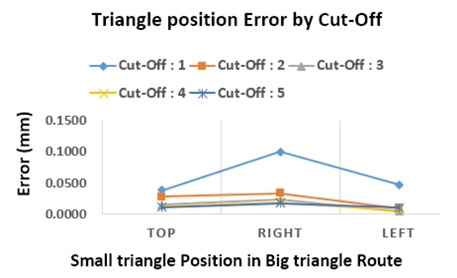
사각형과 동일한 방법으로 대형 삼각형 선을 따라서 빗변이 2 mm 인 소형 삼각형을 가공하여 중심이 대형 삼각형 선상에 존재하는지를 Fig. 9와 같이 측정하였다. Cut-off 값 (6~9)을 배제한 가공 오차에 대한 결과 데이터를 Fig. 10에서 확인할 수 있다. 삼각형 패턴은 직선보간 운동이 발생하여 스캐너 쪽으로 제어신호 비중이 한 단계 증가한 상태인 cut-off 값 4에서 삼각형 중심 위치에 대한 오차의 평균은 12 μm와 표준편차는 6 μm로 측정되었다.

Fig. 9

Triangle line center position

Fig. 10

Triangle position error

4.2 Q-gain에 따른 가공오차

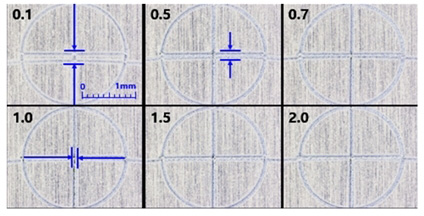
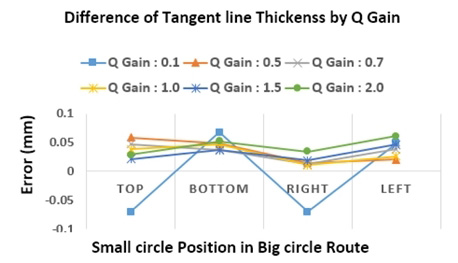
원형패턴에서는 작은 원의 중심선과 큰 원의 접선이 중첩되는 패턴에 대한 두께를 Fig. 11과 같이 측정하였다. 삼각형의 직선 보간 운동보다 원호 보간은 스캐너 빠른 움직임을 더 필요하므로 제어 신호 비중을 스캐너로 한 단계 더 올렸다. Cut-off 값이 3에서 Q-gain 값을 조절하며 측정한 결과를 Fig. 12에서 확인할 수 있다. Q-gain이 1.5일 때 접선에 대한 두께 오차의 평균은 21 μm와 표준편차는 8 μm로 측정되었다.

Fig. 11

Tangent line Thickness & Roundness in Circle

Fig. 12

Circle line position error

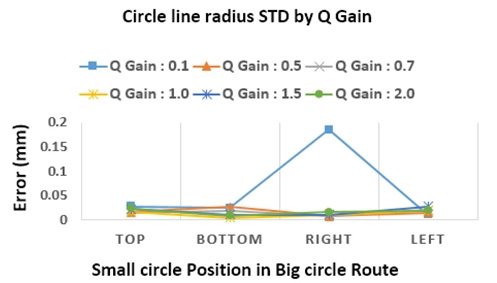
Cut-off 실험에서 도출된 값인 4를 적용하고, Q-gain 값을 0.1~2.0 범위에서 0.5 단위로 값을 조절하며 실험을 진행하였다. circle 중심선에 대한 접선 두께 오차와 진원도 측정을 통하여 가공 오차를 분석하였다. Cut-off 와 동일하게 Fig. 11과 같이 밑그림으로 가공된 대형 원을 따라서 2 mm 크기의 소형 원을 가공하였다. 소형 원의 중심선이 대형 라인의 접선 방향을 지나가는 위치의 두께와 그 편차를 측정한 가공 오차와 4방향으로 반지름을 측정하여 진원도 오차를 Fig. 13과 같이 확인하였다. Q-gain 값이 1.0일 때 원 접선 두께에 대한 오차의 평균은 30 μm와 표준편차는 15 μm로 측정되었으며, 진원도에 대한 오차의 평균은 10 μm와 표준편차는 6 μm로 측정되었다.

실험결과 cut-off 변화에 따른 가공 오차 측정 실험에서 가공 스테이지의 구동 제어신호의 비중이 높아지면서 가공 모양의 정합성이 저하되었다. 그러나 Q-gain의 변화에 따른 가공 모양의 정합성은 크게 변하지 않고 가공 위치의 정확도가 개선되는 효과를 보였다.

Fig. 13

Circle line roundness