연삭공정의 공정모델 개발 및 최적화 방법에 대한 연구


Abstract
In this study, a grinding process roughness model was proposed. To produce the proposed roughness model, the dressing and grinding conditions that affect the roughness were used as variables with respect to previous research results; in addition, the grinding wheel wear after grinding was also considered using these variables. The equation to represent the wear of the grinding wheel was developed using the equivalent chip thickness and time delay between the programmed and actual infeed rate. The proposed roughness model was also used to optimize the grinding process. The dressing and grinding costs, which are a function of time, were used as the cost function to optimize the grinding conditions and a differential evolution algorithm was applied to minimize it. Experiments were carried out to verify the performance of the proposed roughness model and optimization algorithm.
Keywords:
Grinding, Roughness, Optimal, Differential evolution1. 서 론
가공 공정의 최종 단계에서 주로 이루어지는 연삭공정은 가공물의 표면 품질에 직접적으로 영향을 미치는 공정이다. 연삭 작업을 통한 가공물의 표면은 거칠기로 표현되며 이 표면 거칠기를 예측하기 위한 많은 연구들이 진행되어 왔다[1-4]. 기존연구에서 표면 거칠기에 영향을 주는 드레싱 및 연삭조건들이 규명되었으며 이를 바탕으로 연삭프로세스모델들이 개발되었다. 대표적인 연삭 프로세스 모델은 거칠기, 파워(Power), 버닝(Burning) 모델 및 G-ratio 등이 있다[2,5]. 거칠기 및 파워 모델은 드레싱 및 연삭 조건에 따른 공작물의 표면 거칠기 변화를 예측하기 위해 주로 사용되며 버닝 모델은 가공 파워에 따른 공작물의 버닝 유무를 판단할 수 있는 모델로 활용되고 있다[2]. 이 중 표면 거칠기 모델은 연삭공정 후 가공물의 최종 품질을 예측하기 위해 사용되었다[5]. 기존의 표면 거칠기 모델들은 드레싱 조건과 이후 이루어지는 연삭 조건을 일정하게 유지하는 조건으로 표면 거칠기 모델이 개발되었다. 따라서 연삭조건의 변화에 의한 연삭 숫돌의 마모율은 충분히 고려되지 않았다.
일반적으로 연삭 공정은 배치 단위로 연속적으로 이루어지며 일정 배치 작업 후 드레싱 공정을 수행하게 된다. 이러한 배치 단위의 지속적인 연삭 공정에 대한 연산 조건 변경은 최종 제품의 품질 뿐만 아니라 생산비용과도 직결된다. 따라서 연삭 조건 변화에 따른 거칠기 변화와 이로 인한 생산 비용 등을 고려하여 연삭 공정을 설계하여야 한다[6-9]. 본 논문에서는 이러한 배치단위의 연삭 공정을 최적화하기 위해 연삭공정으로 인한 최종 가공물의 품질과 직결되는 거칠기 모델을 개발하였다. 제안된 거칠기 모델식은 연삭 메커니즘을 고려하여 숫돌의 마모변화를 고려할 수 있도록 연삭력에 따른 절입속도의 시간지연 상수를 이용하였다. 개발된 거칠기 모델은 실험을 통해 모델의 적합성을 검증하였다. 또한, 배치단위로 이루어지는 연삭공정의 최적화 방안을 제안하기 위해 드레싱, 황삭, 정삭 및 스파크 아웃동안의 가공비용을 고려한 평가함수를 개발하였다.
본 논문에서 제안한 거칠기 모델식과 평가함수를 기반으로 연삭의 구속조건을 고려한 평가함수의 최적해는 DE (Differential Evolution) 알고리즘을 이용하여 구하고 실험을 통해 그 성능을 검증하였다.
2. 연삭공정의 거칠기모델
연삭공정을 나타내는 주요한 모델은 가공 파워와 거칠기 모델이 대표적이다. 가공 파워는 연삭숫돌과 공작물사이의 수직하중 사이의 관계를 나타내며 이는 숫돌의 드레싱 및 연삭 조건에 따라 차이를 나타낸다. 일반적으로 가공 파워는 드레싱 후 연삭이 진행됨에 따라 선형적으로 증가하는 경향이 있다[1,2]. 이러한 가공 파워를 나타내는 다양한 모델들 중 기존에 연구된 가공 파워 모델의 파라미터에 대한 영향도 분석을 통해 식 (1), (2)와 같이 개발된 모델을 본 논문에서는 적용하였다[2].
| (1) |
| (2) |
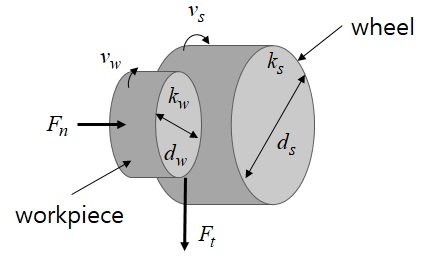
여기서 ad는 드레싱 두께, sd는 드레서의 이송속도, F0, p1, p2, p3, p4, λ0, λ1 그리고 λ2는 모델상수이고, dw 는 공작물 지름, ds는 연삭숫돌의 지름, υs는 연삭숫돌 속도, heq는 등가 칩 두께, 이다.
기존의 거칠기 모델식은 연삭조건 변화에 대한 거칠기 변화를 실험을 통해 그 상관관계를 정하고 이를 바탕으로 거칠기 모델들이 제안되었다. 그러나 본 논문에서는 기존에 개발된 거칠기 모델의 파라미터를 바탕으로 연삭이 진행됨에 따라 연삭숫돌의 마모를 고려할 수 있는 모델식을 제안하였다. 이를 위해 연삭숫돌의 마모 정도를 등가 칩 두께(equivalent chip thickness)로 표현하고 마모율이 커짐에 따라 연삭에 필요한 가공파워도 증가하는 것으로 가정하여 숫돌의 마모도가 커짐에 따라 연삭 공정에서 입력되는 실제 절입속도(actual infeed rate)와 프로그램된 절입속도(programmed infeed rate) 사이에는 시간 지연이 존재하는 것으로 가정하였다.
연삭이 진행됨에 따라 연삭숫돌의 마모정도를 고려하기 위해 플런지 연삭 과정을 Fig. 1에 나타내었다. 그림에서 연삭공정의 가공파워는 공작물과 연삭숫돌사이의 힘에 의해 다음과 같이 나타낼 수 있다.
| (3) |
가정에서와 같이 연삭숫돌이 마모됨에 따라 실제 절입속도와 프로그램된 절입속도는 시간 지연이 존재함을 고려하기 위해 두 절입속도에 대한 관계를 다음과 같이 나타내었다.
| (4) |
여기서 υ(t)는 실제 절입속도, u(t)는 프로그램된 절입속도 그리고 τ는 시상수이다.
시상수 τ는 연삭력과 절입속도의 시간지연 상수로써 다음과 같이 정의 된다[2].
| (5) |
여기서 는 공작물과 연삭숫돌의 강성계수 합을 의미한다.
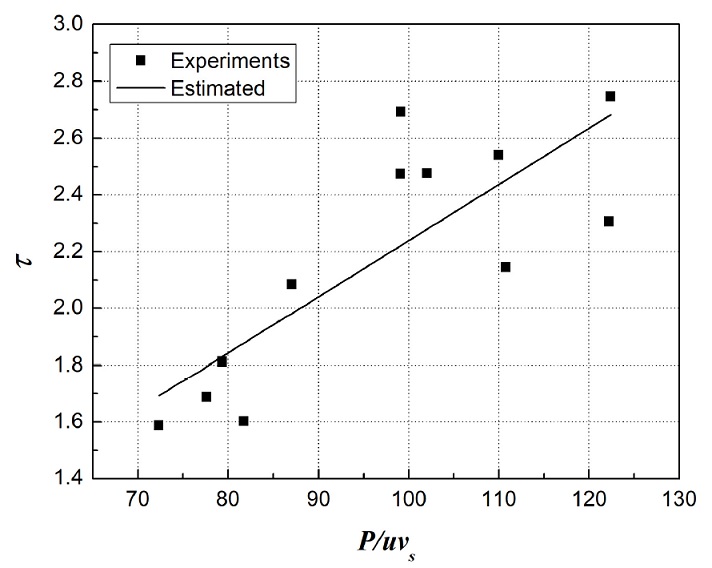
식 (5)의 관계식을 실제 적용하기 위해 프로그램된 절입속도와 연삭숫돌의 회전속도를 바탕으로 실험을 통하여 다음의 관계식을 유도하였다. 실험의 결과는 Fig. 2에 나타내었다.
| (6) |
따라서 기존에 개발된 거칠기 모델식에서 사용되는 등가칩두께는 식 (4)와 (6)을 고려하여 다음과 같이 정의하였다.
| (7) |
이를 바탕으로 연삭 공정의 진행에 따른 연삭숫돌의 마모율을 고려한 플런지 연삭의 거칠기 모델식은 다음과 같이 제안하였다.
| (8) |
여기서 β, γ는 모델 파라미터이고, heq,so는 스파크 아웃 동안의 등가칩두께이다. 그리고 Rr은 드레싱 후 연삭조건 변화에 대한 연삭숫돌의 마모도를 나타낼 수 있도록 다음과 같이 정의 하였다.
| (9) |
여기서 은 누적 절삭량을 나타낸다.
식 (9)를 초기 연삭숫돌의 상태(Rr,0)에서 현재 상태(Rr)까지 정적분하여 연삭이 진행되는 동안의 연삭숫돌의 마모를 다음과 같이 고려하였다.
| (10) |
여기서 ad는 드레싱 두께, sd는 드레서의 이송속도, r, β, fn(n=1,⋯,4) 는 모델 파라미터이고 τs는 시상수이다.
3. 제안된 거칠기 모델식의 파라미터 추정
제안된 모델에 대한 파라미터를 추정하기 위해 G20-50CNC 연삭기와 32A-60-K-VBE 연삭숫돌을 이용하였다. 실험에 사용된 시편은 HRC40경도의 SCM440을 이용하였다.
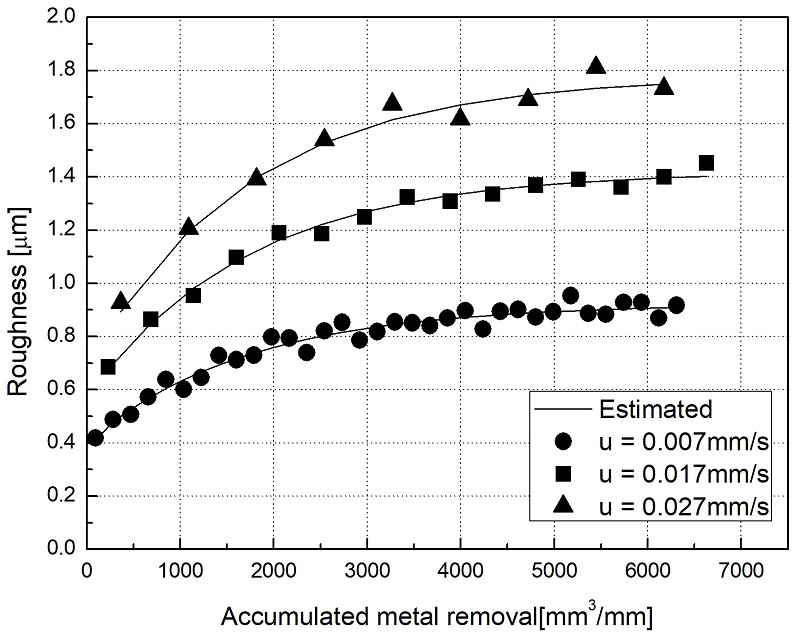
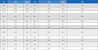
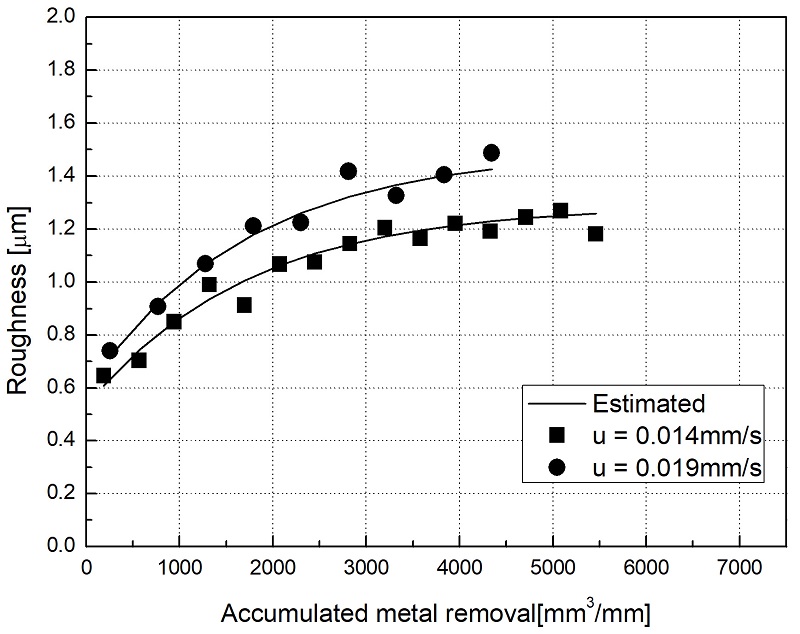
실험의 조건은 절입속도를 0.007 mm/s, 0.017 mm/s 그리고 0.027 mm/s로 변화시켜 실시하여 제안된 모델의 변수를 추정하였다. 이때 적용된 ad, sd 그리고 υs는 0.025 mm, 3.55 mm 그리고 30.48 mm/s로 설정하였다. Fig. 3은 실험을 통해 계측한 거칠기와 추정된 거칠기 변화선도이다. 이때 추정된 파라미터는 Matlab 비선형커버피팅 도구를 이용하였고 추정된 결과는 Table 1에 나타내었다. 모델의 적합성 평가는 결정계수 (R2)를 이용하였고 그 값은 각각 95.56, 94.76 그리고 93.98이다. 제안된 모델의 성능을 검증하기 위해 절입속도를 0.014 mm/s와 0.019 mm/s로 변화시켜 추가 실험을 실시하였다. 실험의 결과와 추정된 거칠기는 Fig. 4에 나타내었다.
4. 연삭프로세스의 최적화
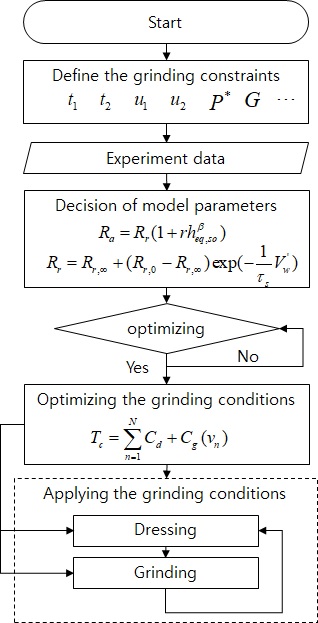
제안된 연삭공정 모델을 바탕으로 배치단위로 이루어지는 연삭공정의 최적화 방안을 제안하였다. 본 논문에서 제안하는 연삭공정의 최적화 절차는 Fig. 5에 나타내었다. 제안된 최적 공정 설계는 앞서 제시한 연삭모델의 모델파라미터를 연삭의 구속조건에 근거하여 실험을 통해 도출하고, 이를 바탕으로 연삭공정의 가공비용에 근거한 평가함수를 통해 최적의 연삭조건이 도출할 수 있도록 제안하였다. 최적화를 위한 평가함수는 황삭, 정삭 및 스파크아웃 동안의 시간을 고려한 연삭비용과 드레싱 비용을 고려하여 다음과 같이 선정하였다.
| (11) |
| (12) |
| (13) |
여기서 Cd과 Cg(υn)은 한 사이클 당 드레싱과 연삭작업에 의해 발생되는 비용을 나타내며, M은 시간당 가공비용, t1, t2, t3는 각각 황삭, 정삭, 스파크아웃 기간, Cs는 단위체적당 사용되지 않는 연삭 숫돌 비용, dw는 공작물의 직경, b 연삭면적의 숫돌 폭, u1, u2는 각각 황삭, 정삭시 절입속도, Gr, Gf는 각각 황삭, 정삭시의 G ratio, Md는 드레싱 비용, Nd 드레싱 간격이다. 그리고 연삭을 위한 연삭 조건은 다음과 같이 υn으로 나타내었다.
| (14) |
여기서 s1은 황삭 절입 깊이, Nd는 드레싱 간격, υs와 υw는 각각 연삭 숫돌 및 공작물의 속도이다.
황삭 및 정삭 가공 시간에 대한 구속조건은 다음과 같다.
| (15) |
여기서 ∆r은 최대 절삭 깊이 이다.
선정된 평가 함수를 바탕으로 실험실 기반의 시험 조건을 고려하여 연삭공정 시 연삭조건의 한계치와 공작물의 버닝 방지를 위한 구속조건은 다음과 같이 선정하였다.
- 절입속도에 대한 구속조건
| (16) |
여기서 u1,u2는 황삭과 정삭 시 절입속도이다.
- 버닝 연삭이 일어나지 않기 위한 가공파워의 구속조건
| (17) |
- G ratio의 구속조건
| (18) |
- 가공파워 및 거칠기에 대한 구속조건
| (19) |
앞서 설계한 평가함수와 연삭 구속 조건을 만족하는 해를 구하기 위해 본 논문에서는 DE알고리즘을 이용하였다[10,11]. DE알고리즘을 적용하기 위해 상태 변수 를 pn개의 균일 분포 랜덤 값으로 초기화 하였다.
| (20) |
여기서 i=1,2,⋯,pn 이고, (j=1,⋯,7)는 부모세대의 연삭조건 υn벡터이다.
부모세대를 통해 생산되는 자손세대는 돌연변이 연산을 통해 구할 수 있다. 돌연변이 연산은 부모 세대에서 중복되지 않는 임의의 벡터를 선정하여 다음의 관계식을 이용하여 수행하였다.
| (21) |
여기서 은 자손세대, r1, r2 그리고 r3는 랜덤 수이다.
돌연변이 연산 후 해집단의 다양성을 확보하기 위해서 재조합연산을 수행한다. 재조합 연산은 와 를 일정 확률로 뒤섞는다.
| (22) |
여기서 0 ≦ CR ≦ 1이다.
재조합 연산 후 생성된 후손 세대를 평가하여 우수한 형질만 선택하여 최종적인 다음 세대로 전이 시킨다. DE 알고리즘의 모든 연산으로 생긴 후손 세대는 앞서 선정한 연삭 구속 조건과 비교하여 구속 조건에 만족하는 값이 생성될 수 있도록 하였다. DE 알고리즘을 적용하여 선정한 최적 연산 조건은 Table 2와 같다.
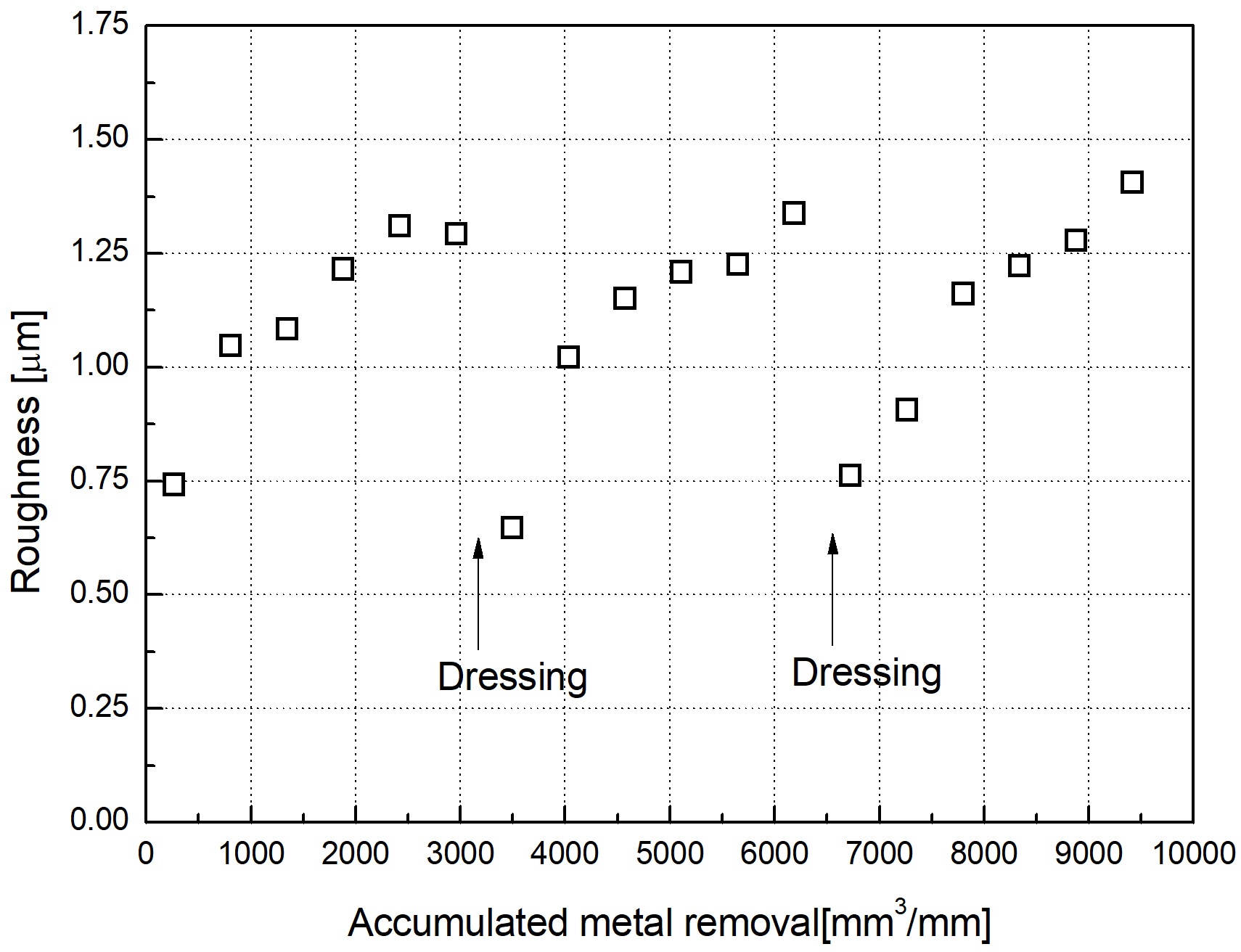
추정된 최적 연삭 조건을 이용하여 실험적으로 그 결과를 검증하였다. 검증을 위한 실험을 3차례에 걸쳐 수행하였고 그 결과를 Fig. 6에 나타내었다. 결과에서 제안된 최적화 알고리즘을 통해 수행한 연삭 작업 동안 그 거칠기 한계인 1.5 µm 이내에서 가공이 이루어짐을 확인하였다.
5. 결 론
연삭 공정은 기계 가공을 한 후 마지막 단계에서 이루어지는 공정으로 최종 제품의 품질과 직결되어 있어 숙련된 작업자의 경험에 근거하여 공정 조건을 결정하여 사용한다. 이로 인해 배치 단위로 이루어지는 연삭공정의 최적화 방안을 적용하기는 다소 어려운 부분이 많다. 따라서 본 논문에서는 연삭공정을 통한 공작물의 표면 거칠기를 예측할 수 있는 모델을 제안하였다. 제안된 모델식은 연삭공정이 진행됨에 따른 공작물의 표면거칠기가 연삭 숫돌의 마모 정도를 고려할 수 있도록 하였다. 마모 정도를 표현하기 위해 등가 칩두께를 모델 변수로 활용하였고 절입속도를 변화시켜 제안된 거칠기 모델식의 파라미터를 실험을 통해 구하였다. 또한 제안된 모델식을 바탕으로 배치단위 연삭공정의 최적화 알고리즘을 제안하였다. 최적 연삭 조건 선정을 위해 가공시간을 함수로 한 가격함수를 제안하였고 인공지능 알고리즘 중 하나인 DE알고리즘을 적용하여 이를 최적화하였다. 제안된 최적화 알고리즘은 연구실 기반의 실험조건에 근거하여 개발되었지만, 실제 산업현장의 연삭조건과 큰 배치(batch) 단위의 연삭 작업에서 비 숙련자라 하더라도 최적의 기계가공을 위한 가이드라인으로 충분히 활용될 수 있을 것이다.
논문에서 제안한 거칠기 모델식의 파라미터는 절입속도 변화만을 고려하여 추정하였으나, 향후 추가적인 실험 조건 변화에 대한 검토를 바탕으로 제시된 모델의 변수 변화와 거칠기 값의 변화에 대한 상관관계를 연구할 예정이다.
Acknowledgments
본 논문은 동아대학교 교내연구비 지원에 의하여 연구되었음.
References
- Markin, S., 2008, Grinding Technology: Theory and Application of Machining with Abrasives, John Wiley & Sons, New York.
-
Choi, T. J., Subrahmanya, N., Shin, Y. C., 2008, Generalized Practical Models of Cylindrical Plunge Grinding Process, International Journal of Machine Tools and Manufacture, 48:1 61-72.
[https://doi.org/10.1016/j.ijmachtools.2007.07.010]

-
Xiao, S., Markin, S., 1996, On-line Optimization for Internal Plunge Grinding, CIRP-Manufacturing Technology, 45:1 287-292.
[https://doi.org/10.1016/S0007-8506(07)63065-0]

-
Botcha, B., Rajagopal, V., Ramesh, B., Bukkapatnam, S.T.S., 2018, Process-machine Interactions and Multi-sensor Fusion Approach to Predict Surface Roughness in Cylindrical Plunge Grinding Process, Procedia Manufacturing, 26 700-711.
[https://doi.org/10.1016/j.promfg.2018.07.080]

-
Ahrens, M., Damm, J., Dagen, M., Denkena, B., Ortmaier, T., 2017, Estimation of Dynamic Grinding Wheel Wear in Plunge Grinding, Procedia CIRP, 58 422-427.
[https://doi.org/10.1016/j.procir.2017.03.247]

-
Lee, K. M., Hsu, M. R., Chou, J. H., Guoa, C. Y., 2011, Improved Differential Evolution Approach for Optimization of Surface Grinding Process, Expert Systems with Applications, 38:5 5680-5686.
[https://doi.org/10.1016/j.eswa.2010.10.067]

-
Gopan, V., Win, K. L. D., Surendran, A., 2018, Integrated ANN-GA Approach For Predictive Modeling And Optimization Of Grinding Parameters With Surface Roughness As The Response, Materialstoday, 5:5 12133-12141.
[https://doi.org/10.1016/j.matpr.2018.02.191]

-
Baskar, N., Saravanan, R., Asokan, P., Prabhaharan,G., 2004, Ants Colony Algorithm Approach for Multi-objective Optimization of Surface Grinding Operations, International Journal of Advanced Manufacturing Technology, 23 311-317.
[https://doi.org/10.1007/s00170-002-1533-6]

-
Rana, P., Lalwani, D. I., 2017, Parameters Optimization of Surface Grinding Process Using Modified & Constrained Differential Evolution, Materialtoday, 4:9 10104-10108.
[https://doi.org/10.1016/j.matpr.2017.06.329]

-
Zhou, Y., Li, X., Gao, L., 2013, A Differential Evolution Algorithm with Intersect Mutation Operator, Appl Soft Comput, 13:1 390-401.
[https://doi.org/10.1016/j.asoc.2012.08.014]

- Babu, B.V., Jehan, M. M. L., 2003, Differential Evolution for Multi-objective Optimization, The 2003 congress on evolutionary computation, https://10.1109/CEC.2003.1299429.