4 패드 저널 베어링 2상 유동 2-FSI 해석
Abstract
A four-pad journal bearing is used to support high-speed, high-load turbine generators. The direct lubrication type has the merits of low power loss, low pad temperature, and high load capacity. Direct lubrication offers the additional advantages of good vibration and anti-shock characteristics. The simulation of bearings of this type requires two-phase fluid analysis because the fluid consists of a mixture of oil and air. Apart from this, because of the movement of the rotor and tilting pad, two-phase two-fluid structure interaction (2-FSI) simulation is required to determine the final locations of the rotor and pads. Finally, based on these locations, a static simulation is conducted to determine the temperature, pressure, and the oil and air distribution. The rotor moves 0.5 mm in the direction of negative gravity and the tilting pad rotates 0.09, 0.035 degrees with a minimum gap of 78 mm and maximum pressure of 10 MPa.
Keywords:
2-Way fluid structure interaction, 4 Pad journal bearing, 2 Phase fluid, CFD1. 서 론
터빈 발전기에 사용되는 터빈을 지지하는 저널 베어링은 유압을 이용하여 지지되는 방식이다. 회전축을 지지하기 위해서 패드를 사용하게 되는데 사용되는 패드 개수에 따라서 다양한 타입이 있다. 4패드 저널 베어링은 높은 하중을 지지하면서 작동하며 오일에 의해서 유막이 형성되고 이를 통해서 회전축을 지지하는 방식이다. 유체 윤활을 통해서 지지하며 틸팅패드 베어링은 고하중 지지, 흡진성, 내충격성 면에서 우수하다고 알려져 있다[1]. 이러한 이유 때문에 제작, 설계상 어려움, 고가의 비용에도 불구하고 우수한 안정성 때문에 터빈과 같은 고속안정성이 필요한 장비에 사용되고 있다. 대다수 경험에 의지하여 설계를 진행하고 있는 상황이며 일부 설계 프로그램을 이용해서 설계를 진행하고 있지만 많은 단순화와 가정이 있고 2상 유동 해석은 제대로 반영이 되지 않고 2-FSI 역시 일부만 반영을 하는 상황이다. 이러한 점을 극복하고자 2상 유동(2 phase fluid)과 2-FSI (fluid structure interface)를 고려한 해석을 진행하여 틸팅 패드 베어링의 해석기술을 확보하여 베어링 성능을 정확히 예측하고자 연구를 진행하였다.
2. 4 패드 틸팅 베어링 구조
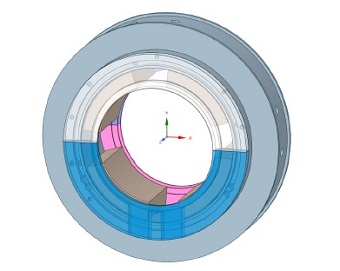
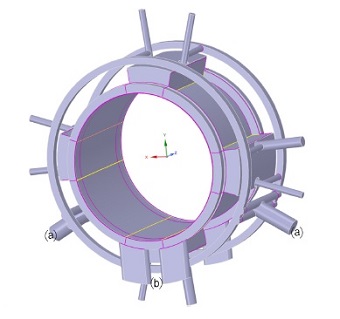
4개의 패드가 약간의 회전이 가능한 구조를 가지면서 회전축을 지지하는 구조를 가지고 있다. Fig. 1은 이번 연구 대상인 4패드 저널 베어링을 나타낸다. 상부에 2개, 하부에 2개의 틸팅 패드를 가지고 있다. 각각의 틸팅패드 사이에는 오일 분사를 위한 노즐이 설치되어 있다.
4패드 틸팅 베어링의 요구 성능은 Table 1같다.
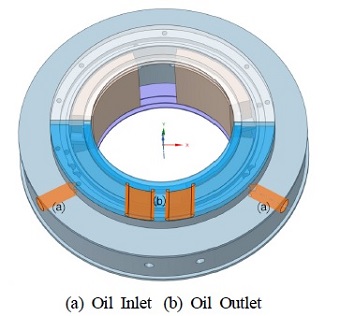
공급되는 오일은 VG32 등급의 오일을 사용한다. 오일은 하부에 있는 두 군데서 공급되고 공급된 오일은 회전축을 따라서 회전하다가 축과 베어링 틈새를 통해서 외부로 배출되거나 두 군데 배기구멍을 통해서 배출된다. Fig. 2에 오일 공급 구멍과 출구가 표시 되어 있다.
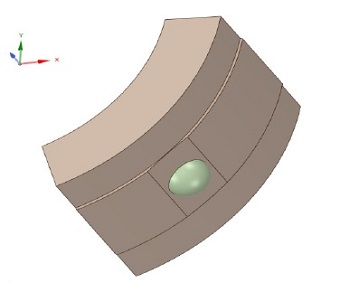
4개의 틸팅 패드는 볼 소켓 연결 방식으로 연결되어 있으며 Fig. 3은 볼 소켓 구조를 나타낸다. 8개의 노즐을 통해서 오일이 회전축에 공급이 되는 직접 윤활 구조를 가지고 있다. 직접 윤활 구조는 동력 손실 저감, 패드 온도 저감, 하중 용량 증가 등의 장점이 있다. 노즐에서 공급된 오일은 공기 중에 분사되고 오일은 회전축을 따라서 회전을 하게 되고 이를 통해서 회전축과 패드 사이에 유막이 형성된다.
3. CFD 해석
3.1 2-Phase 해석
베어링에 공급되는 오일은 Fig. 4와 같은 유체영역을 흐르게 된다. (a)에서 공급된 오일은 바깥쪽 원형 라인을 타고 흐르다 네 군데 오일 공급 포켓에 도달하게 되고 여기에 있는 8개 분사 노즐을 통해서 오일이 공급되는 구조를 가지고 있다. 공기와 오일이 동시에 존재하기 때문에 유체 베어링에서는 2상 유동 해석을 해야 한다.
다상 유동은 2개 이상의 상이 존재하는 경우를 의미한다. 화학 성분이 다른 공기+오일, 같은 화학 성분이지만 열역학적 상이 다른 증기+액상과 같은 경우를 말한다. 다성분(multi component)과 다상(multi phase)에 대한 구분도 필요하다. 다성분은 분자 수준의 혼합을 얘기하며 이 경우 유체는 하나의 유체로 간주하고 해석을 수행한다. 다상은 거시적 관점에서의 혼합을 얘기하며 각각의 상에 대한 온도와 속도에 대한 해석이 필요하다.
속도, 온도와 같은 특성이 각각의 상에 따로 존재하게 되는데 이들은 열, 물질전달, 계면력(interfacial force)을 통해서 계면(interface)을 통해서 서로의 특성을 전달하게 된다. 다상 유동을 해석하기 위한 유체 모델은 각각의 상이 속도, 온도, 난류를 공유하는 Homogeneous 모델과 압력만 공유하고, 속도, 온도, 난류 등은 각각의 상에 있어서 서로 다른 Inhomogeneous 모델이 있다[2].
계면 설정 모델은 dispersed, mixture, free surface 방법이 있다. Dispersed 모델은 물속에 존재하는 공기방울과 같이 하나의 연속된 유체에 다른 유체가 분리되어 존재하는 경우, Mixture 모델은 가장 기본적으로 사용되는 모델이면서 각 상들을 대칭적으로 다루는 모델이다. Free surface 모델은 각각의 상이 경계면으로 구분이 되는 경우에 사용된다. 계면을 통해서 전달되는 특성값들은 접촉면에 비례하게 되며 이 값은 계면면적밀도(interfacial area density)로 나타낸다.
Dispersed model은
Mixture model은
Free surface 모델은
A: interfacial area density
α,β: phase
dβ: mean diameter
rβ,rα: volume fraction
3.2. 2-Way FSI 해석
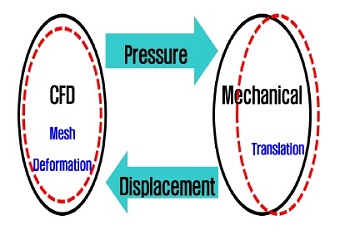
저널 베어링을 해석하기 위해서는 FSI (fluid structure interface) 방법을 적용해야 한다. FSI는 유체영역과 고체영역을 동시에 고려해서 문제를 풀어가는 해석 기법을 말하며 1-way 방법과 2-way 방법이 있다. 1-way 방법은 유체영역을 해석한 후에 여기서 구해진 압력값을 이용해서 고체영역을 해석하는 방법을 말한다. 고체부의 변화에 의한 유동장의 변화는 고려되지 않기 때문에 단방향 해석이라 불린다. 오직 유동장만 해석하고 이를 이용해서 고체부분이 어떻게 변화하는지 파악하는 경우에 사용하는 방법이다. 2-way, 양방향 해석은 유동해석에서 압력 값이 고체쪽으로 전달되고 이로 인해서 고체가 변화하고 고체의 변위값이 다시 유체쪽으로 전달되어 유동영역의 메쉬가 변화하게 된다. 변화된 메쉬로 인해서 유체의 각 성분들이 변화하게 되고 이렇게 변화된 값은 다시 고체 쪽으로 전달되어 고체와 유체가 상호작용하면서 동시에 유동영역과 고체영역을 해석하는 방법을 말한다. Fig. 5은 유동해석과 구조해석 서로 교환하는 데이터 종류와 흐름을 나타내고 있다. 저널 베어링은 rotor 무게로 인해서 이동하게 되고 이때 틸팅 패드도 움직이게 된다. 이때 유막이 변화하면서 공극의 압력장이 변화하게 되고 압력의 변화에 의해서 틸팅패드와 rotor가 동시에 움직이기 때문에 단방향으로 해석이 불가하고 양방향해석을 수행해야 한다. 이처럼 CFD 해석과 구조해석을 동시에 수행해야 정확한 해석이 가능하다.
3.3 CFD 이론해석
저널 베어링에 사용되는 지배 방정식은 다음과 같다[2].
1) 연속 방정식
| (1) |
2) 운동량 방정식
| (2) |
3) 에너지 방정식
| (3) |
ρ: 밀도
uj: 속도
keff: 열전도도
E: 총에너지
τij: 전단응력텐서
난류를 직접적으로 계산하기에는 현실적은 많은 무리가 따른다. 메쉬를 아주 미세하게 한다고 해도 난류의 length scale을 실제적으로 모사하기는 무리가 따르게 된다. 난류는 통계적 기법을 이용하여 모델링을 하게 되는데 평균과 변화량을 이용하여 Navier Stokes 방정식을 RANS (Reynolds averaged navier stokes)로 변화하여 단순화하는 방법을 사용한다. 본 논문에서는 SST (shear stress transport) 난류 모델을 사용하였다. 이 모델은 k-w모델에 기반을 둔 난류 모델이면서 역 압력 구배 상태에서 유동박리를 잘 모사하는 것으로 알려져 있다. SST는 모델은 제한기를 설치하여(limiter) 다른 모델이 eddy viscosity를 과도하게 계산하여 유동박리를 정확히 예측하지 못하는 단점을 보완한 모델이다.
3.4 유동 해석 조건
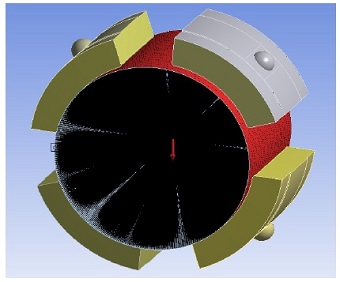
저널 베어링의 유동 영역에 대한 메쉬는 Fig. 6에 나타내었다. 로터와 만나는 유동 영역에 회전 조건 3600 rpm을 주고 입구 조건에 mass flow rate 1.5 kg/s 온도 45도, 출구 조건으로 opening 조건을 인가하였다. 2-FSI 해석을 수행하기 위해서는 초기 조건을 주고 해석 하는 것이 해석 수렴성과 해석 시간 저감에 도움이 된다. 초기 조건 해석을 위해서 정적 해석을 동일한 경계 조건을 유지 한 채 먼저 해석 진행하였다. 로터는 원점에서 중력 방향으로 0.2 mm 이동 시킨 후에 해석 진행하였다. 노드 1,721,962, 요소 7,464,478이다. 2상 유동 해석을 위한 조건은 homogeneous, free surface을 선택하였으며 난류 모델은 SST를 사용하였다[3,4]. 로터의 회전에 의한 작동유의 온도 상승을 보기 위해서 Viscous work 조건을 사용하여 점성에 의한 온도상승을 고려하였다. 작동 유체는 공기와 VG32 오일을 사용하였으며 패드와 로터 사이의 좁은 틈새에는 메쉬가 6개 정도 생성되도록 하였다. 4개 패드와 로터가 만나는 부분은 메쉬가 이동 되는 조건을 부여하여 고체부와 2-FSI 해석이 가능하도록 조건을 부여하였다. 해석은 ANSYS CFX와 ANSYS Mmechanical, system coupling을 사용하여 해석 진행하였다[5].
3.5 구조해석 조건
구조 해석을 위한 조건은 Fig. 7와 같다. rotor 중심에 하중이 가해지고 rotor와 틸팅 패드 사이에 접촉 조건을 인가하였으며 마찰 계수는 통상적 금속면 사이의 마찰계수 0.1을 사용하였다. 재질은 stainless steel, white metal을 사용하였으며 메쉬는 모두 육면체 메쉬가 생성되도록 하였다. 노드 29,269, 요소 28,631이다. 하중을 인가하고 최종 0.025초 동안 과도응답 해석을 수행하였다. 시간 간격은 7e-5초로 설정하였다. rotor의 표면과 틸팅 패드 베어링 부분을 system coupling 해석을 위한 조건으로 선정하였다. 틸팅을 고려하기 위해서 틸팅 패드 베어링의 볼 위치에 자유롭게 회전할 수 있도록 볼 소켓 조건을 인가하였다. 유동영역에서 선정한 system coupling 영역과 고체영역에서 선정한 system coupling 영역은 FSI 해석 진행 중에 압력과 변위 데이터를 서로 주고받게 되는 영역이다.
4. 해석 결과
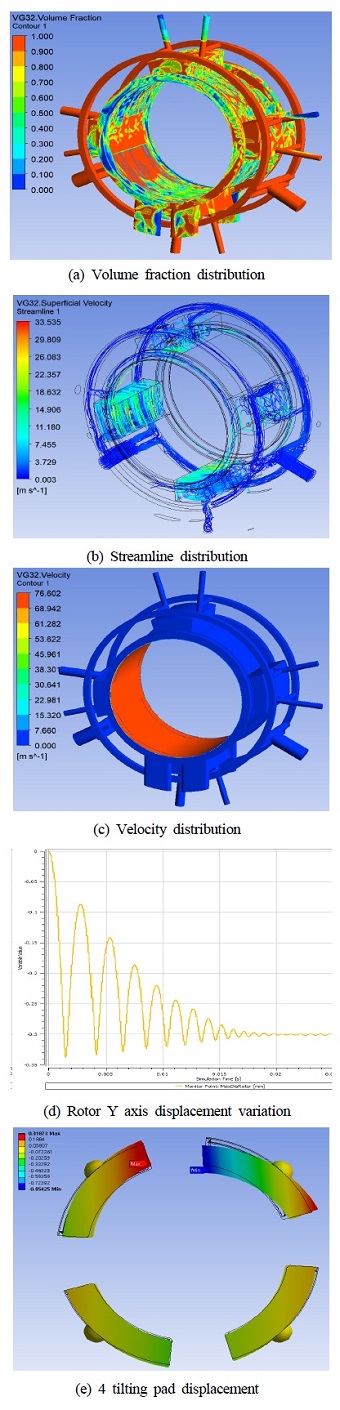
2-FSI 해석은 24시간 소요 되었으며 Fig. 8(a)는 오일과 공기가 분포되어 있는 모습을 나타내고 있으며 (b)는 오일 입구에서 시작되는 유선의 흐름을 나타내고 있으며 (c)는 오일의 속도 분포를 나타내고 있다. (d)는 해석 중 로터가 어떻게 움직이는 지를 나타내는 그림이다. 로터가 초기에 약간의 진동을 하다가 안정화 되는 것을 볼 수 있다. 로터는 중력 방향으로 0.3 mm 이동하는 것으로 계산되었다. 로터는 원점위치에서 중력 방향으로 0.2 mm 이동을 시킨 상태에서 해석을 진행했기 때문에 전체 이동 거리는 원점에서 0.5 mm 이동한 것이다. Fig. 8(e)는 왼쪽 하부는 틸팅패드는 0.09도, 오른쪽 하부는 0.035도 회전한 것으로 계산되었다.
4.1 회전축, 패드 이동을 고려한 유동 해석
2상 유동, 2-FSI 과도 응답 해석을 통해서 로터의 이동량과 로터의 회전각도량을 계산하게 된다. 이렇게 계산된 결과를 바탕으로 유동영역과 고체영역에 대한 모델링을 수정하고 다시 메쉬작업을 하고 유동해석을 수행하였다. 정적 유동 해석을 수행하였으며 해석 조건은 기존과 동일하게 유지 하였다. 이러한 해석을 수행하는 이유는 온도예측을 정확히 하기 위해서이다.
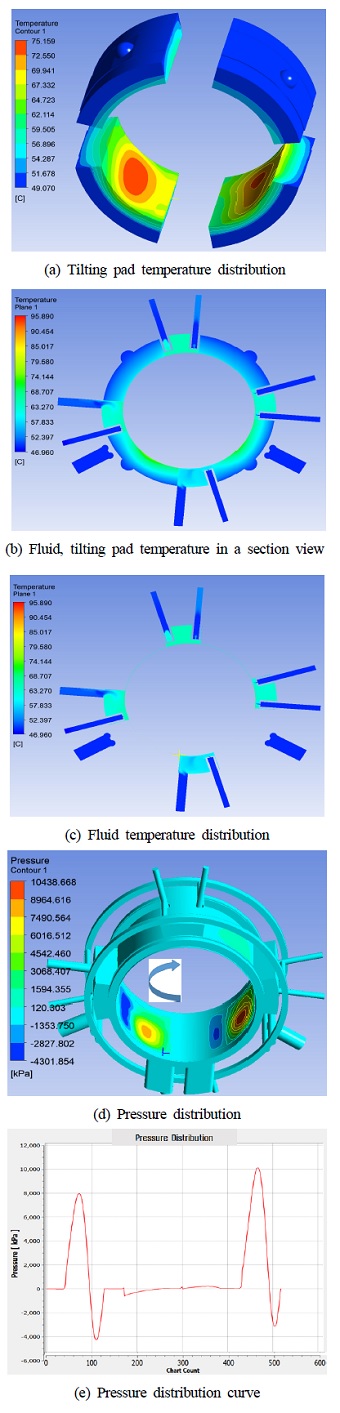
Fig. 9에 해석 결과를 나타내었다. (a) 고체부, 로터와 틸팅 패드의 온도분포를 나타낸다. (b) 단면으로 나타낸 고체부의 온도 분포, (c) 오일 부분의 온도 분포를 단면으로 나타낸다. (d) 유체부의 압력 분포를 나타낸다. (e) 압력 분포 곡선을 나타내며 (d) 나타낸 화살표 방향처럼 6시 방향부터 반시계 방향으로의 압력 분포를 나타낸다. 틸팅패드의 최고 온도는 75.2도, 최고 압력은 10 MPa로 계산되었다. 틸팅 패드과 회전 축 사이의 최소 공극은 78 um로 계산되었으며 위치는 왼쪽 하부 틸팅패드와 회전축 사이에 존재한다[6].
4.2 설계 프로그램과 해석 결과 비교
베어링 제작사의 자체 설계 프로그램과 해석 결과와의 비교는 Table 2와 같다. 이 설계 프로그램을 이용해서 베어링 설계에 적용해 왔다. 이러한 설계 프로그램은 빠르게 계산이 가능하다는 장점이 있지만 베어링 각 부분에 대한 값을 정확히 볼 수 없다는 단점과 설계 프로그램에서 제공하는 몇 가지 경우에 대해서만 설계가 가능하다는 단점이 있다. 이에 반해서 FEA를 이용하면 필요한 부분에 대한 값을 볼 수 있고 다양한 모델에도 해석이 가능하다는 장점이 있다. 4패드 베어링과 FEA 결과를 비교 했을 때 10% 이내의 오차를 가지고 있음을 알 수 있다.
5. 결 론
4 패드 저널 베어링에 대한 베어링 성능을 예측하기 위한 2상, 2-FSI 해석을 수행하였다. 4패드 저널 베어링에 대한 해석은 공기와 오일이 같이 존재하기 때문에 2상 유동해석이 필요하며 패드와 회전축이 동시에 움직이기 때문에 유동과 고체를 같이 해석하는 2-FSI 해석을 수행하였다. 회전축은 중심에서 0.5 mm 이동하는 것으로 계산되었으며 최소 공극은 78 um으로 계산되었다. 온도와 압력을 확인하기 위해서 정적 상태의 해석을 추가로 진행하였으며 하부 패드에서 생성되는 최고압력은 10 MPa로 계산되었다. 이렇게 계산된 결과를 베어링 제작사의 설계 프로그램과 비교하였으며 그 결과는 10% 이내에 들어오는 것을 확인하였다.
References
- Dong Yang Metal Co., 2019, Final Project Report of Complex Generation Steam Turbine 16 Tilting 2-Pad Bearing Development, Government Project Report sponsored by Ministry of SMEs and Startups, KOREA, RBS18009.
- Taesung S&E, 2015, CFX User’s Manual, Taesung S&E, Seoul.
-
Dhande, D. Y., Pande, D. W., 2017, A Two-Way FSI Analysis of Multiphase Flow in Hydrodynamic Journal Bearing with Cavitation, Journal of the Brazilian Society of Mechanical Sciences and Engineering, 39 3399-3412.
[https://doi.org/10.1007/s40430-017-0750-8]

- Kerlekar, R., Dhande, D., Nigade, N., Kondhalkar, G., 2015, Performance Analysis of 3 Lobe Hydrodynamic Journal Bearing, International Journal of Engineering Research and General Science, 3:4 1097-1101.
-
Yang, J. I., Palazzolo, A., 2019, 3D Thermo-Elasto-Hydrodynamic CFD Model of a Tilting Pad Journal Bearing-Part I: Static Response, ASME. Journal of Tribology, 141:6 061702.
[https://doi.org/10.1115/1.4043349]

-
Geller, M., Schemmann, M., Kluck, N., 2014, Simulation of Radial Journal Bearings Using the FSI Approach and A Multi-Phase Model with Integrated Cavitation, Progress in Computational Fluid Dynamics, 14:1 14-23.
[https://doi.org/10.1504/PCFD.2014.059196]


Professor in the Department of Mechanical Engineering, Yonam Institute of Technology.His research interest is CFD, Sound & Vibration.
E-mail: Shin7@snu.ac.kr