[ Papers ]

Journal of the Korean Society of Manufacturing Technology Engineers - Vol. 29, No. 6, pp.481-488

ISSN: 2508-5093 (Print) 2508-5107 (Online)

Print publication date 15 Dec 2020

Received 21 Oct 2020 Accepted 04 Nov 2020

DOI: https://doi.org/10.7735/ksmte.2020.29.6.481

원통 복합재 쉘의 비선형 좌굴에 의한 파괴현상 연구

조희근^a^{, *}

Fracture Phenomenon of Cylindrical Composite Shell by Nonlinear Buckling

Hee Keun Cho^a^{, *}

aDepartment of Mechanical Engineering Education, Andong National University

Correspondence to: ^*Tel.: +82-54-820-5677 E-mail address: hkcho@anu.ac.kr (Hee Keun Cho).

Abstract

A cylindrical shell is a representative structure that exhibits buckling. To investigate the nonlinear behavior of this shell, the arc-length method or load– displacement control Newton–Raphson numerical analysis method is used. In this study, the buckling and post-buckling phenomena of composite shells were investigated, and the fracture phenomena of composites were evaluated for their load–displacement behaviors. Composite buckling is a complex process compared to those of isotropic materials. Moreover, in the case of a laminated composite material, it is difficult to accurately identify the time and place at which a failure might occur because various stress components and interlayer shear stresses interact with each other. Using the arc-length nonlinear numerical analysis method, the failure phenomena were clearly identified along the behavioral path of the composite shell after buckling, and the differences were confirmed via various composite failure theories.

Keywords:

Composite, Buckling, Nonlinear, FEA

1. 서 론

강화섬유와 기지재로 구성된 복합재는 그 구조적 특성상 비강도 및 비강성이 매우 우수할 뿐만 아니라 기존의 철 구조물에 비해서 경량화가 가능하므로 첨단산업 분야에 많이 적용되고 있는 실정이다. 특히 항공 및 우주분야의 구조물에서는 복합재의 사용이 필수적이라 할 수 있다. 원통형 혹은 패널형의 복합재 구조물을 설계할 때 반드시 고려하여야 하는 것 중의 하나는 좌굴 현상이다. 좌굴현상은 국부적으로 발생하기도 하며 그 거동이 매우 비선형적이고, 구조물의 신뢰성에 심각한 영향을 미치기 때문에 오랜시간 많은 연구자에 의해 연구되어 왔다^[1-4].

복합재의 좌굴(buckling) 및 좌굴후(post-buckling) 현상에 대한 기존 연구는 Cho^[5], Zhou^[6], Baiz^[7], Anders^[8] 등에 의해 수행되었다. 기존의 연구는 복합재의 하중, 변위, 응력, 변형율 등의 변화 및 현상에 집중되었다. 좌굴은 궁극적으로 재료의 파괴를 유발하기 때문에 그 해석과 분석에 있어서 세심한 주의가 필요하다. 복합재가 좌굴점을 지나 좌굴후 극심한 비선형 거동을 하는 동안 급격한 응력의 변화를 동반하게 되며, 위치와 시간에 따라서 순간적으로 설계 기준점을 벗어나게 된다. 적층복합재의 경우 재료의 파괴는 다양한 위치에서 발생 가능하며, 특히 다층으로 구성된 복합재 중간층에서 국부적으로 파괴가 발생하는 경우, 육안으로 구조물의 신뢰성을 검증하는 것은 거의 불가능하다.

본 연구에서는 적층복합재 쉘의 비선형 좌굴후 거동에 있어서 복합재 파괴현상을 규명하였다. 이를 위하여 복합재 좌굴후 거동을 해석하기 위한 유일한 비선형 해석 방법인 arc-length 수치해석 방법을 사용하였다. 또한 적층복합재의 파괴를 정량적으로 평가하기 위하여 기존의 Tsai-Wu, maximum stress, maximum strain 등의 파괴 이론을 적용하였다.

2. 수치해석

2.1 복합재 쉘요소^[9]

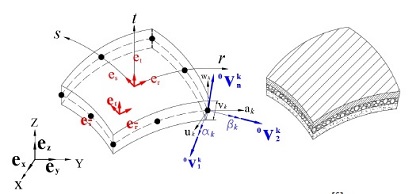
복합재 원통형 쉘의 유한요소 해석을 위하여 8절점 쉘요소를 사용하였다. Fig. 1에 나타낸 바와 같이 쉘요소는 각절점당 5개의 자유도를 가지고 있다. 3축 병진, 면에 접하는 2개의 회전변위 벡터이다.

Fig. 1

3D 8-node laminate shell element[5]

쉘요소는 막(membrand) 변형과 굽힘(bending) 변형을 동시에 표현할 수 있는 요소로써 그 이론적 배경은 다음과 같다. 각 절점의 변위는 병진과 회전 자유도의 조합으로써 식(1)과 같이 나타낼 수 있다.

x i t = ∑ k = 1 n h k x t k t + t 2 ∑ k = 1 n a k h k V ∋ k t

(1)

여기서 시간을 나타내는 t는 실제 시간이 아니라 가상의 순서 및 계산 시점을 의미한다. t, 0, t+△t에서 각각의 변위 u는 다음과 같이 나타낼 수 있다.

u i t = x i t - x i 0

(2)

u i = x i t + ∆ t - x i t

(3)

식(1)을 식(2)와 식(3)에 대입하여 정리하면 다음과 같다.

u i t = ∑ k = 1 N h k u i k t + t 2 ∑ k = 1 n a k h k V n t k - V n t k 0

(4)

u i = ∑ k = 1 N h k u i k + t 2 ∑ k = 1 n a k h k V n i k

(5)

여기서 방향벡터 V는 식(6)과 같다.

V n i k = V n i k t + ∆ t - V n i k t

(6)

식(4)는 총합 변위를 계산하기 위한 식이며, 식(5)의 변위를 계산하기 위해서는 방향벡터 ^tV₁^k, ^tV₂^k 를 정의하고 이 두 벡터의 외적벡터는 ^tV_n^k이다. 이 수직벡터와 쉘요소의 절점의 접선벡터의 관계식은 다음과 같다.

V 1 k t = e 2 × V n k t / e 2 × V n k t

(7)

V 2 k = t V n k t × V 1 k t

(8)

V n k = - V 2 k t α k + V 1 k t β k

(9)

여기서 α_k, β_k는 각각 노드점에서의 쉘 면에 접하는 접선벡터 ^tV₁^k, ^tV₂^k에 대한 회전각도이다. Total Lagrangian 방법에 의한 비선형 변위증분은 식(10)과 같이 나타낼 수 있다. 변위 증분에 의한 새로운 노드점의 좌표는 다음계산을 위한 기준점이 된다.

u i = ∑ k = 1 N h k u i k + t 2 ∑ k = 1 N a k h k - V 2 i k t α k + V 1 i k t β k

(10)

변위의 증분에 의한 업데이트된 쉘 면의 수직벡터는 식(11)과 같다.

V n k t + Δ t = V n k t + ∫ α k, β k - V 2 k d α k + τ V 1 k d β k τ

(11)

Total Lagrangian 비선형 유한요소해석에서, 각 노드점의 변위를 자연 좌표계 r,s,t에 대하여 미분하는 관계식은 식(12)와 같다.

u i, r u i, s u i, t = ∑ k = 1 N = h k, r 1 t t g 1 i k t t g 2 i k h k, s 1 t t g 1 i k t t g 2 i k h k, t 1 t t g 1 i k t t g 2 i k u i k α k β k

(12)

여기서

g 1 i k t = - 12 a k t V 2 i k, g 2 i k t = 12 a k t V 1 i k

(13)

Fig. 1에 나타낸 쉘요소의 후크의법칙은 {σ}= [C^'_sh]{ϵ}로 나타낼 수 있다. 복합재 쉘요소의 재료강성 행렬 [C^'_sh]는 아래의 식(14)와 같다.

C s h' = C ¯ 11 C ¯ 12 0 C ¯ 14 00 C ¯ 21 C ¯ 22 0 C ¯ 24 00 000000 C ¯ 41 C ¯ 42 0 C ¯ 44 00 0000 C ¯ 55 C ¯ 56 0000 C ¯ 65 C ¯ 66

(14)

재료의 강성행렬은 적층각도에 따라서 강성이 변한다. 식(15)에서 m=cosθ_(j), n=sinθ_(j), 각도 θ는 재료의 기준 좌표축으로부터 주물성치 좌표축(principal material axis) 까지 측정한 각도이며, j는 복합재의 적층 순서를 나타낸다.

C ¯ 11 = m 4 Q - 11 + 2 m 2 n 2 Q 12 + 2 Q 44 + n 4 Q 22 C ¯ 12 = m 2 n 2 Q 11 + Q 22 - 4 Q 44 + m 4 + n 4 Q 12 C ¯ 14 = m n m 2 Q 11 - n 2 Q 22 - m 2 - n 2 Q 12 - 2 Q 44 C ¯ 22 = n 4 Q 11 + 2 m 2 n 2 Q 12 + 2 Q 44 + m 4 Q 22 C ¯ 24 = m n n 2 - m 2 Q 22 + m 2 - n 2 Q 12 + 2 Q 44 C ¯ 44 = m 2 n 2 Q 11 + Q 22 - 2 Q 12 + m 2 - n 2 Q 44 C ¯ 55 = m 2 Q 55 + n 2 Q 66 C ¯ 56 = m n Q 66 - Q 55 C ¯ 66 = m 2 Q 66 + n 2 Q 55

(15)

여기서Q 는 구조의 강성을 나타내며 각 항목에 대한 구체적인 수식의 표현은 식(16)과 같다. Q는 종탄성계수 E, 포와송비 υ 그리고 횡탄성계수 G의 조합으로 표현된다. 쉘요소는 일반적인 3차원 요소이므로 방향에 따른 강성을 모두 각각 계산해야 한다.

Q 11 = E 11 1 - ν 12 ν 21; Q 22 = E 22 1 - ν 12 ν 21 Q 12 = ν 12 E 22 1 - ν 12 ν 21 = ν 21 E 11 1 - ν 12 ν 21 Q 44 = G 12 Q 55 = G 23 K p Q 66 = G 13 K p

(16)

여기서 K_p는 전단계수(shear factor)로써 두께 방향으로 곡선형의 전단응력을 일정한 응력으로 변환시켜주기 위한 계수이다^[10]. 일반적인 광역 좌표계 x,y,z에서 재료강성행렬의 좌표변환은 식(17)과 같다.

C s h = T s h T C s h' T s h

(17)

식(17)에서 [T_sh]는 좌표축의 회전변환 행렬이다.

2.2 Arc-length 비선형 수치해석

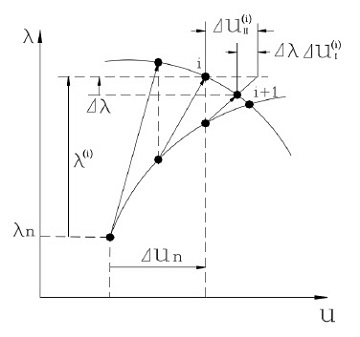
비선형 유한요소 수치해석 알고리즘으로 가장 많이 사용되는 것이 Newton-Raphson과 arc-length 방법이다. 비선형 좌굴후 현상해석에 있어서는 일반적으로 snap-back과 snap-through 현상이 발생한다. 이러한 현상들이 발생하는 좌굴후 비선형해석에 Newton-Raphson 방법은 적합하지 않다. Arc-length 방법은 일정한 영역내에서 해를 점진적으로 찾아가는 방법으로써 비선형성이 강한 좌굴 해석에 특화되어 있는 알고리즘이라 할 수 있다. Fig. 2는 arc-length 방법에 의해서 비선형 해를 점진적으로 찾아가는 방법을 나타낸 것이다.

Fig. 2

Arc-length nonlinear search[11]

여기서 i는 반복수를 나타내고, n은 해석의 스탭을 그리고 λ는 하중 계수를 나타낸다. 이것을 사용하여 비선형 평형 방정식으로 표현 하면 다음과 같다.

K n i Δ u i = λ R n - F n i - 1

(18)

식(18)를 비선형 증분형 식으로 나타내면 식(19)과 같다.

K i Δ u i - Δ λ R = λ n + λ i R - F n i - 1 = - P i

(19)

여기서 변위는 Fig. 2에 나타낸 △u_Ⅰ과 △u_Ⅱ 부분의 변위조합에 의해서, 각 해석 스텝에 있어서 반복회수에 따른 변위증분을 구할 수 있다.

Δ u i = Δ λ Δ u I i + Δ u I I i

(20)

Δ u I I i = - K i - 1 P i

(21)

임의의 해석단계에 있어서 i번째 반복계산의 변위 증분형 벡터를 정의하면 다음과 같다.

t i = Δ u n + β λ i

(22)

2.3 복합재 파괴이론

섬유강화 복합재는 일반적으로 섬유와 기지로 구성되어 있기 때문에 파괴현상이 복잡하다. 따라서 기존에 다양한 복합재 파괴 이론들이 제시되었다^[12]. 본 연구에서는 최대변형율(maximum strain), 최대응력(maximum stress) 및 Tsai-Wu 파괴이론 기준에 대해서만 검토하였다.

i) 최대변형율 이론

최대변형율 파괴이론에서는 파괴변형율과 실제변형율의 비율이 재료의 주재료좌표계에서 비교된다.

f = max ⁡ ϵ 1 X ϵ, ϵ 2 Y ϵ, ϵ 3 Z ϵ, γ 21 S ϵ, γ 13 R ϵ, γ 23 Q ϵ

(23)

여기서 S_ϵ는 1-2 평면, R_ϵ 는 1-3평면, Q_ϵ는 2-3평면의 전단파괴 변형율을 각각 나타낸다.

ii) 최대응력 이론

최대응력파괴이론은 최대변형율 파괴 이론과 유사하게 재료의 기준 좌표계에서 실제응력과 파괴응력의 비율로써 파괴상태를 결정한다.

f = max ⁡ σ 1 X, σ 2 Y, σ 3 z, τ 21 S, τ 13 R, τ 23 Q

(24)

여기서 S는 1-2 평면, R는 1-3평면, Q는 2-3평면의 전단파괴 응력을 각각 나타낸다.

iii) Tsai-Wu 이론

Tsai와 Wu가 1971년에 발표한 적층복합재 파괴이론으로써 응력의 파괴표면을 다음과 같이 정의하였다.

f = σ 12 X t X c + σ 22 Y t Y c + σ 32 Z t Z c + τ 122 S x y 2 + τ 132 S x z 2 + τ 232 S y z 2 - 1.0 σ 1 σ 2 X t X c Y t Y c - 1.0 σ 2 σ 3 Y t Y c Z t Z c - 1.0 σ 1 σ 3 X t X c Z t Z c + σ 1 1 X t - 1 X c + σ 2 1 Y t - 1 Y c + σ 3 1 Z t - 1 Z c

(25)

이 밖에도 적층복합재의 파괴 이론은 Hill, Norris, Ashkenazi, Hankinson, Cowin, Fischer 등 다양한 연구자에 의해 제시되었다^[12].

3. 적층복합재 패널 좌굴후 현상해석

3.1 해석 모델

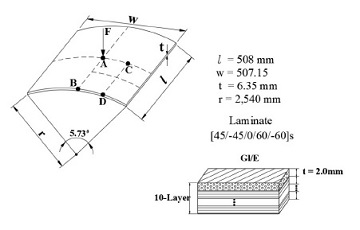
단순 지지를 받는 원통형 쉘 패널의 해석 모델을 대상으로 하여 좌굴 및 좌굴후 현상에 대한 거동을 계산하였다. Fig. 3에 나타낸 바와 같이 반경 r=2540 mm, 길이 l=508mm, 두께 t=2mm인 원통형 패널 모델은 좌굴이 쉽게 발생하는 형상적 특성을 가지고 있다. 패널의 양단은 단순지지로 고정되는 경계조건이 주어졌고, 두께방향으로 E-glass epoxy GFRP prepreg 10층이 적층된 적층복합재 패널이다. 적층레이업은 [30/-30/90/60/-60]S으로 대칭 레이업이다.

Fig. 3

Composite shell arch panel

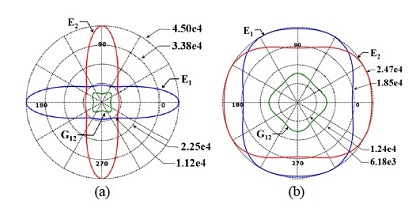
따라서 각층의 두께는 0.2 mm이다. 직교이방성인 prepreg는 재료의 기준 각도에 대한 파이버의 각도 변화에 따라 기본 물성인 종탄성계수(E)와 횡탄성계수(G)가 변한다. 뿐만 아니라 이러한 prepreg를 여러 층으로 적층한 경우 전체복합재의 대표 물성인 E₁E₂G₁₂ 또한 각도에 따른 함수이다. Fig. 4에 해석에 사용된 prepreg와 10층 레이업 복합재의 방향에 따른 물성 변화 함수를 각도 좌표계로 나타내었다.

Fig. 4

Material stiffness of (a) Gl/E prepreg and (b) Laminate

제시된 10층 적층복합재의 경우 대칭 레이업이기 때문에 굽힘변형이 발생할 때 비틀림이 발생하지 않는다. 또한 종탄성계수와 횡탄성 계수 모두 0도와 90도 기준선을 중심으로 대칭적 현상을 나타낸다.

Fig. 3에 나타낸 모델을 Fig. 1에 나타낸 쉘요소를 사용하여 유한요소로 분할하였다. 분할된 요소의 수는 576개, 노드의 수는 1,825개이다. 쉘요소는 굽힘과 막 변형의 거동을 충분히 신뢰할 만한 수준으로 표현할 수 있다. 이러한 해석 모델과 같이 두께가 얇은 경우 매우 효율적으로 적용될 수 있으며, 8절점 quadratic 요소의 경우는 그 신뢰성이 더욱 높다. 본 연구에서는 좌굴 후 거동에 있어서 복합재의 파괴 현상을 규명한다. 따라서 2.4절에서 적용될 복합재 이론을 제시하였고, 이러한 파괴이론을 사용하여 파괴유무를 판단하기 위해서는 다양한 물성치가 필요하다. Table 1에 사용된 Gl/E prepreg의 다양한 물성치가 제시되었다.

Table 1

Material properties of epoxy E-glass UD

Table 1에서 X_t와 X_e는 각각 X 방향의 인장강도와 압축강도를 나타내고, S,Q,R는 각각 1-2 평면, 2-3평면, 3-1평면의 전단강도를 나타낸다. 이 부호 규약은 변형율에도 그대로 적용되어, X_ϵt, X_ϵc는 각각 X방향의 최대 인장변형율과 최대 압축변형율을 나타낸다. S_ϵ,Q_ϵ,R_ϵ도 각각 1-2 평면, 2-3평면, 3-1평면의 최대 전단변형율을 의미한다. Table 1에서 제시한 재료의 물성치를, 복합재의 파괴 유무를 계산하는 기본 데이터로 사용한다.

3.2 좌굴후 거동에 의한 복합재 파괴

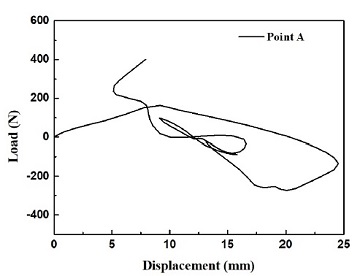
원통형 쉘의 경우는 좌굴현상을 가장 명확하게 나타내는 대표적인 구조형상이다. 좌굴후 거동에서 특히 snap-back과 snap-through 현상을 가장 빈번하게 발생시킨다. snap-back과 snap-through 현상이 발생하는 거동을 계산하는 것은 앞에서 언급한 바와 같이 일반적인 Newton-Raphson 방식에 의해서는 해석이 불가능하며 arc-length방법에 의해서만 가능하다. 특히 적층복합재의 좌굴후 현상은 그 거동 경로가 등방성재료에 비해서 매우 불규칙하고 복잡하다. 먼저 Fig. 3에 제시된 모델에서 A점에 하중을 가하여 좌굴 현상을 발생시키고 이때의 하중-변위 거동을 계산하였다.

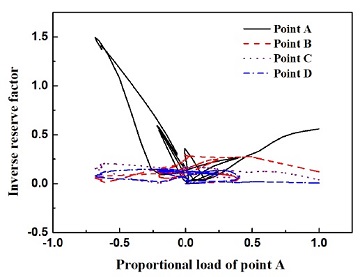
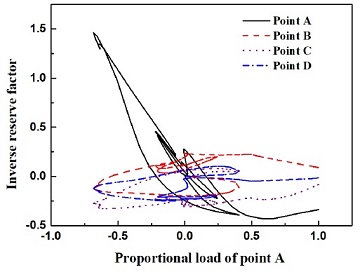
해석모델의 A점에 하중을 가했을 때 좌굴후 거동에 대한 하중-변위 관계를 Fig. 5에 나타내었다. 이때의 변위는 수직 변위이다. Fig. 5에서 알 수 있는 바와 같이 적층복합재의 좌굴후 거동은 매우 복합한 경로를 나타낸다. 복잡한 경로를 따라서 거동을 할 때 복합재의 어느 한 부분에서 순간적으로 복합재의 응력이 한계점을 초과하여 파괴가 발생할 수 있다.

Fig. 5

Load vs. displacement of laminate post-buckling

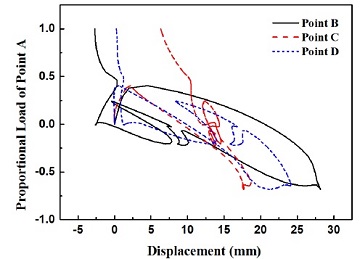
적층복합재 구조물의 파괴는 면밀히 검토하지 않으면 발견하기가 매우 어려우며 이러한 이유 때문에 큰 재난으로 이어지는 경우가 종종 있다. Fig. 6은 A점에 하중이 가해질 때 B, C, D 점에서의 변위를 나타낸다. 이때 A점에서 가해지는 하중은 Fig. 5에서 알수 있는 바와 같이 최대 400 N이며 이것을 –1과 1사이의 비율로 나타내었다. 변위의 경로를 자세히 관찰하면 다수의 불연속점이 있으며 경로 또한 매우 복잡하게 얽혀 있다. 이러한 불연속점은 순간적으로 접히는 현상을 의미한다. 복합재의 파괴를 정량적으로 나타내기 위하여 inverse reserve factor (IRF)를 정의하였다. IRF는 부과된 극한하중에 대한 극한강도의 상대비로 나타내기 때문에 IRF의 값이 1보다 크면 복합재가 파괴된 것을 나타내고, 1보다 작으면 안전한 것을 의미한다.

I R F = F u l t i m a t e F s t r e n g t h

(26)

Fig. 6

Load vs. displacement of laminate post-buckling

2.4절에서 제시한 최대변형율 파괴이론, 최대응력 파괴이론 및 Tsai-Wu 파괴이론의 세 가지 경우에 대하여 적층복합재 쉘의 좌굴후 거동에 있어서 파괴의 관점에서 검토하였다. 복합재의 파괴는 국부적으로 혹은 순간적으로 발생하기 때문에 하중-변위 전체 경로를 따라서 계산해야 한다. 해석에 사용된 레이업은 이미 언급한 바와 같이 [45/-45/0/60/-60]S이다. Fig. 3에 표시된 A, B, C, D의 네 점에서 파괴를 검토하였으며 이때 대상이 된 복합재 층은 맨 위층 30° 각도 층이다. A점에 400 N의 하중을 가하였고 arc-length 방법으로 60 스탭으로 해석을 수행하였다.

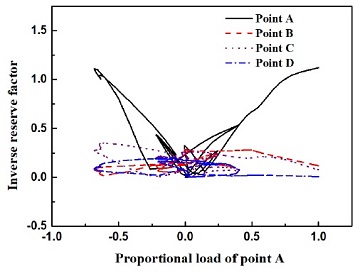
원통형 쉘의 정중앙인 A점에 하중이 가해질 때, 하중의 상대적 비율에 따른 좌굴후 거동에서의 복합재 파괴를 계산한 결과를 Fig. 7, 8, 9에 나타내었다.

Fig. 7

IRF of maximum strain failure criterion (top layer)

Fig. 8

IRF of maximum stress failure criterion (top layer)

Fig. 9

IRF of Tsai-Wu failure criterion (top layer)

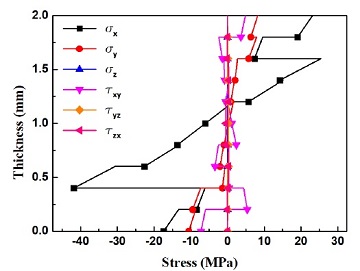
Fig. 7, 8, 9는 각각 최대변형율, 최대응력, Tsai-Wu 파괴조건에 대한 IRF 결과를 나타낸다. A점에 가해지는 400 N의 하중 비율에 대한 A, B, C, D 네 점에서의 IRF는 Fig. 7, 8, 9에서 보는 바와 같이 랜덤한 경로를 그리며 변화한다. 또한 파괴기준에 따라서도 다소 상이한 결과를 나타낸다. Fig. 7의 최대변형율이론 결과에 의하면 하중비율이 –0.5 및 1 부근에서 IRF가 1을 초과함으로 파괴가 발생했다. 반면 최대응력이론 및 Tsai-Wu이론 결과에서는 –0.5 부근에서는 IRF가 1을 초과함으로 파괴가 발생하지만 1부근에서는 IRF가 1보다 낮아서 안전한 것으로 나타났다. 좌굴후 거동에 있어서 어느 일정한 시간 영역에서 복합재 파괴가 발생하는 현상을 본 해석 방법론과 수치해석 절차에 의하여 계산을 완료하였다. 또한 이러한 파괴는 미소 영역, 각 층, 일정한 구간 영역에서 독립적으로 발생하기 때문에 설계 시 매우 주의하여야 한다. 널리 알려진 바와 같이 적층복합재는 각 층별 응력의 양상이 불연속적인 현상을 나타내다. A점에서의 2 mm 두께에 발생하는 맨 마지막 단계 계산(400 N 하중상내)에서 응력의 변화를 Fig. 10에 나타내었다. 6개 응력성분을 광역 직교좌표계를 기준으로 계산하였다.

Fig. 10

Stress through thickness at A point

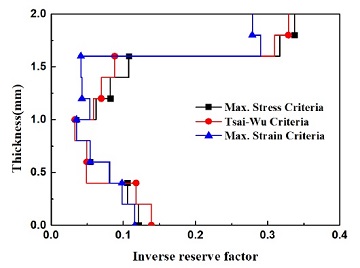
파괴의 기준으로 판단하는 IRF의 값도 각 층별 불연속적인 값으로 나타난다. Fig. 11은 쉘의 2 mm 두께를 통하여 계산된 IRF의 값을 각 파괴이론에 대한 계산값을 나타낸다. 최대변형율, 최대응력 및 Tsai-Wu의 이론 계산 값은 서로 비슷한 양상을 보이지만 쉘의 맨 아래층과 맨 윗 층에서는 다소 상이함을 알 수 있다.

Fig. 11

IRF through thickness at A point

4. 결 론

현재까지 좌굴후 거동에 있어서 적층복합재의 파괴에 대한 연구는 많이 수행되지 않았다. 본 연구에서는 적층복합재 원통형 쉘의 좌굴 현상에 대한 파괴를 정량적으로 계산하는 이론적 배경, 절차, 방법론을 제시하였고 그 수치해석 결과를 제시하였다. 10층의 E-glass epoxy 적층복합재 패널에서 좌굴이 발생할 때 매우 복잡한 하중-변위 경로를 나타내는데 이것을 arc-length 비선형 해석 방법을 적용하여 계산하였다. 이때 하중-변위 거동 경로를 따라 복합재 파괴를 나타내는 정량적 변수 값을 계산하여 구조물의 파괴/안전 유무를 규명하였다. 최대변형율이론, 최대응력이론, Tsai-Wu이론의 세 가지 파괴이론을 적용하여 계산한 결과를 서로 비교 검토하여 그 차이점과 유사점을 본문에 자세하게 제시하였다.

본 연구결과는 추후 적층복합재 원통형 쉘 구조물을 설계하는데 있어서 매우 핵심적인 자료를 제공할 수 있을 뿐만 아니라 복합재의 비선형 좌굴후 현상 연구에서도 훌륭한 참고 자료가 될 것이다.

Acknowledgments

이 논문은 안동대학교 기본연구지원사업에 의하여 연구되었음.

References

Shivakumar, K. N., Whitcomb, J. D., 1985, Buckling of a Sublaminate ina Quasi-Isotropic Composite Laminate, J. Comp. Mater., 19:1 2-18. [https://doi.org/10.1177/002199838501900101]
Beakou, A., Touratier, M., 1993, A Rectangular Finite Element for Analysing Composite Multilayered Shallow Shells in Statics, Vibration and Buckling, Int. J. Num. Meth. Eng., 35:4 627-653. [https://doi.org/10.1002/nme.1620360406]
De Faria, A. R., 2002, Buckling Optimization and Antioptimization of Composite Plates: Uncertain Loading Combinations, Int. J. Num. Meth. Eng., 53:3 719-732. [https://doi.org/10.1002/nme.309]
Palazotto, A. N., Linnemann, P. E., 1991, Vibration and Buckling Characteristics of Composite Cylindrical Panels Incorporating the Effects of a Higher Order Shear Theory, Int. J. Solids and Struct., 28:3 341-361. [https://doi.org/10.1016/0020-7683(91)90198-O]
Cho, H. K., 2018, Nonlinear Buckling and Post-Buckling of Cylindrical Composite Structure Using Degenerated Shell Element, J. Korean Soci. of Manuf..Tech. Eng., 27:6 577-583. [https://doi.org/10.7735/ksmte.2018.27.6.577]
Zhou, Y., Stanciulescu, L., Eason, T., Spottswood, M., 2015, Nonlinear Elastic Buckling and Postbuckling Analysis of Cylindrical Panels, Finite Element in Analysis and Design, 96 41-50. [https://doi.org/10.1016/j.finel.2014.12.001]
Baiz, P. M., Aliabadi, M. H., 2010, Post Buckling Analysis of Shear Deformable Shallow Shells by the Boundary Element Method, Int. J. Num. Meth. Eng., 84:4 379-433. [https://doi.org/10.1002/nme.2898]
Anders, M., 2001, Analysis of Post-Buckling Branches at Multiple Symmetric Bifurcations, Int. J. Num. Meth. Eng., 51:4 413-428. [https://doi.org/10.1002/nme.157]
Bathe, K. J., 1982, Finite Element Procedures in Engineering Analysis, Prentice-Hall, New Jersey.
Cho, H. K., 2016, The Effects of composite Laminate Layups on Nonlinear Buckling Behavior Using a Degenerated Shell Element, J. Korean Soc. of Manuf., Proc. Eng. 15:1 50-60. [https://doi.org/10.14775/ksmpe.2016.15.1.050]
Cho, H. K., 2018, Nonlinear Buckling Analysis of GFRP Laminated Composite Panels, J. Korean Soc. Adv. Comp. Struc., 9:4 1-7. [https://doi.org/10.11004/kosacs.2018.9.4.001]
Sih, G. C., Skudra, A. M., 1983, Failure Mechanics of Composites, North-Holland, New York.

Hee Keun Cho

Professor in the Department of Mechanical Engineering, Andong National University.His research interest is computer aided engineering, finite element method, composite materials and design optimization

E-mail: hkcho@anu.ac.kr

Material Properties	Value
E_x (MPa)	45000
E_y (MPa)	10000
E_z (MPa)	10000
G_xy (MPa)	5000
G_yz (MPa)	3846.2
G_xz (MPa)	5000
V_xy	0.3
V_yz	0.4
V_zx	0.3
X_t (MPa)	1100
X_c (MPa)	-675
Y_t (MPa)	35
Y_c (MPa)	-120
Z_t (MPa)	35
Z_c (MPa)	-120
S (MPa)	80
Q (MPa)	46.1
R (MPa)	80
X_ϵt	0.0244
X_ϵc	0.015
Y_ϵt	0.0035
Y_ϵc	0.012
Z_ϵt	0.0035
Z_ϵc	0.012
S_ϵ	0.016
Q_ϵ	0.012
R_ϵ	0.016