OIS 액츄에이터 평가 시스템 개발

1. 서 론

손떨림 방지 기술은 기계적인 방법이나 이미지 프로세싱을 이용하여 진동 등의 외란에 대한 촬영물의 선명도를 보정하는 기술이다^[1-3]. 손떨림 방지 기술에는 광학식 손떨림 방지(optical image stabilization, OIS)와 디지털 손떨림 방지(digital image stabilization, DIS)가 있는데^[1], 디지털 손떨림 방지 기술은 촬영물을 직접 처리하여 소프트웨어 단계에서 보정하는 방법이고, 광학식 손떨림 방지 기술은 자이로 등의 속도/위치 센서를 이용하여 렌즈, 이미지 센서의 위치를 흔들림에 반대되는 방향으로 이동시켜 촬영물의 블러링을 사전에 방지하는 방법이다. 이 중 OIS 방식을 통한 촬영물이 일반적으로 더 높은 품질을 가지고 있어서, 최근 출시되는 스마트폰은 OIS 방식을 많이 채택하고 있다^[2,3].

일반적으로 스마트폰에 사용되는 OIS는 손떨림을 감지하는 자이로스코프, 구동 드라이버, 보이스코일 모터와 홀센서(hall effect sensor)를 포함한 액츄에이터와 이를 제어하는 마이크로컨트롤러 등으로 구성되어 있다. OIS의 개발 과정은 자이로스코프나 드라이버, 마이크로 컨트롤러를 담당하는 반도체와, 보이스코일 모터와 홀센서, 구동 기구를 제작하는 액추에이터 업체, 이미지센서 업체, 렌즈 업체, 이를 조립하는 모듈 업체의 협업으로 이루어진다. 스마트폰 OIS에 관련해서는 각 부분 별로 연구가 이루어지는데, 최근에는 병진형과 회전형 액추에이터의 구조에 관련한 연구^[4,5], 강인제어나 2자유도 제어등 제어 성능에 관한 연구^[6,7], 효율적인 저비용, 저전력 반도체의 구현에 연구^[8] 등이 이루어져 왔다.

OIS의 최종 성능의 평가 방법에는 OIS 모듈 단위에서 실제 손 떨림과 유사한 진동 외란에 대해 이미지를 측정하여 억압비를 측정하는 방법을 이용한다. 그러나, 중간 개발 단계에서 영상 처리나 자이로스코프 성능을 배제하고, 제어 관점에서 추종 성능을 통하여 외란 억제 성능을 확인하여 액추에이터를 평가하게 된다. 이러한 추종 성능은 기계적 성능과 제어 성능이 결합된 결과라 볼 수 있다. OIS 전체 모듈이 아닌 액추에이터를 설계하고 개발하는 업체의 경우, 직접 제어기를 개발하지 않기 때문에 시제를 평가하는 데 어려움이 있다. 액추에이터 업체가 시제품을 제작하면, 제어기 업체에서 성능을 평가하고, 이를 통해 제품 개선의 과정을 반복하는 경우가 많다. 본 연구에서는 액추에이터 업체의 관점에서 시제품에 대하여 복잡한 구성없이 독립적인 환경에서 액추에이터의 동특성을 파악하고, 직접 제어 알고리즘을 구현하여, 액추에이터의 성능을 평가할 수 있는 시스템을 개발하였다. 하드웨어와 소프트웨어의 개발을 통하여 동특성을 평가하고, 기본적인 제어 이론을 기반으로 제어기를 설계하고 이를 직접 테스트할 수 있는 시스템을 구축하였다. 또한, 이를 GUI로 구현하여, 기구 설계 엔지니어가 어려움이 없이 사용할 수 있게 하였다.

2. 하드웨어 분석 및 identification

2.1 액추에이터 개루프 주파수 응답 측정

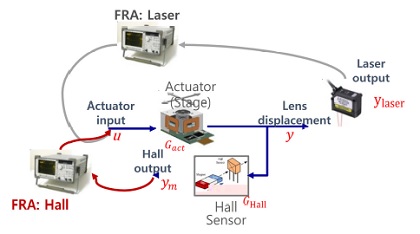
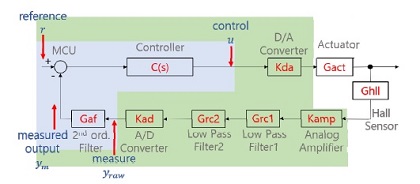
본 연구에서 고려하는 OIS 액추에이터는 볼 스테이지 타입으로, X-Y 스테이지가 직렬적으로 구성되어 있으며, 보이스코일에 의해 구동되며, 홀센서에 의해 이동 변위가 측정된다^[8]. OIS 액추에이터의 특성을 파악하려면, 개루프(open-loop) 주파수 응답에 분석하는 것이 필요하다. 이 과정은 본 시스템 개발 전에도 Fig. 1과 같이 개루프 측정 환경을 구축하여, 액추에이터 입력으로부터 홀센서 출력값까지의 주파수 응답과 레이저 변위계의 출력값까지의 주파수 응답을 측정하였다. 이를 활용하면 액추에이터와 홀센서의 동적 특성을 분석하게 된다. 만약 레이저 변위계를 사용하여 실제 변위를 측정한 경우에는 액추에이터와 홀센서의 특성을 명확히 구분할 수 있지만, 별도의 환경이 구성되어야 하므로, 홀센서 출력만 측정하는 경우가 많다.

Fig. 1

OIS open-loop bode measurement setting

Fig. 1의 블록 선도에서 나타낸 것과 같이 액추에이터의 기계적 전달 함수를 G_act, 홀센서 전달 함수를 G_hall, 레이저 변위계의 감도를 K_laser라고 할 때 액추에이터 입력으로부터 홀센서 출력값까지의 응답은 G_act⋅G_hall로, 레이저 변위계까지의 응답은 G_act⋅K_laser로 나타낼 수 있다. 이 때 홀센서의 응답을 별도로 중요하게 고려하는 것은 액추에이터 입력(정확히는 보이스코일모터 입력)이 직접적으로 홀센서의 출력에 영향을 주는 직접 전달 항(direct transmission term)이 존재하기 때문이다^[9]. 따라서, 액추에이터에서 홀센서로의 응답y_m/u에서 레이저 변위계까지의 응답y_laser/u을 나누어 식 (1)과 같이 액추에이터와 홀센서의 응답을 각각 구할 수 있다.

$\[ \begin{array}{l}\begin{array}{cc}\left(\mathrm{Hall response}\right)& \frac{y_m}{u}=G_{act}\cdot G_{hall}\end{array}\\ \begin{array}{cc}\left(\mathrm{Laser response}\right)& \frac{y_{laser}}{u}=G_{act}\cdot K_{laser}\end{array}\end{array} \]$

(1)

2.2 액추에이터 전달함수 추정

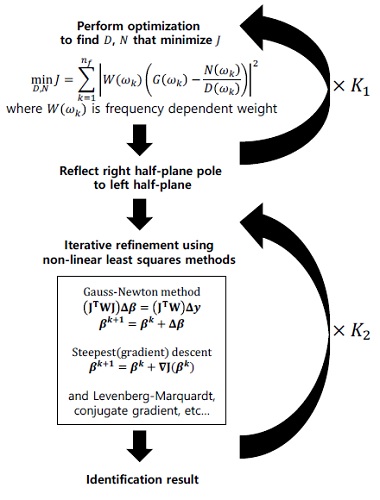
액추에이터 및 홀센서의 주파수 응답으로부터 전달함수를 식별하였다. 시스템 식별은 공칭 응답에 대해 복소영역에서 비선형 최적화과정을 통해 이루어지며, S-K iteration을 통한 일차적인 최적화 후 안정(stable) 영역에서의 최적화를 위해 우반평면(right half plane)에 위치한 극점을 좌반평면(left half plane)으로 이동시킨 다음 비선형 최소제곱 방법을 통해 반복적으로 모델을 개선하게 된다^[10,11]. Fig. 2는 전달함수 추정 과정을 나타내며, 최종적으로 주파수 응답으로부터 안정적인 전달함수를 얻게 된다.

Fig. 2

Model identification process

2.3 제어기 하드웨어 개발 및 시스템 블록 구성

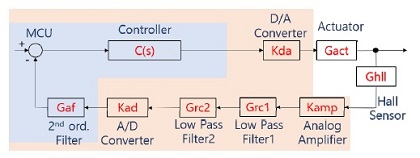
범용적인 제어환경 구성을 위해 노드 스위칭에 따라 다양한 구조선택이 가능하도록 제어 보드를 제작하였다. 보드에 아날로그 증폭회로와 저주파 필터 회로 등이 내장하였으며, 마이크로 컨트롤러(TMS320F28335, TI사, 미국)에서 inverse 필터(주파수에 의존적인 홀센서의 이득을 일정하게 유지)와 notch 필터, PID/lead-lag/custom 제어기를 조합하여 사용할 수 있으며 각각의 파라미터를 변경할 수 있다. 별도의 컴파일 없이 RS-232 통신 명령어를 통하여 제어구조의 조합과 파라미터를 변경할 수 있도록 펌웨어를 개발하였다. 이밖에 제어보드에는 OIS의 동작과 연관되는 AF (auto focusing) 설정부, PC와 통신부 등이 있다.

Fig. 3은 제어 보드의 H/W와 S/W를 블록화한 것과 2.2절에서 언급한 액추에이터, 홀센서의 전달 함수를 통합하여 폐루프(closed loop)를 구성한 것이다

Fig. 3

Control system structure

제어기를 설계하고 폐루프 특성을 분석하기 위해서는 Fig. 3의 시스템 구성을 일반적인 형태의 블록다이어그램으로 정리할 필요가 있다. 따라서 식 (2)와 같이 제어기, 플랜트(plant), 센서(sensor) 블록으로 정리하였다.

$\[ \begin{array}{l}C\left(s\right)=C\left(s\right)\\ G\left(s\right)=K_{da}\left(s\right) G_{act}\left(s\right)\\ H\left(s\right)=G_{hall}\left(s\right) K_{amp}\left(s\right) G_{rc1}\left(s\right) G_{rc2}\left(s\right) K_{ad}\left(s\right) G_{af}\left(s\right)\end{array} \]$

(2)

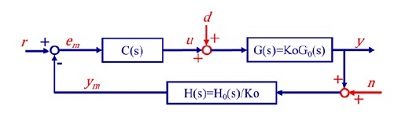
안정성 분석을 위하여 외란 d과 노이즈 n를 추가하였으며, 추종 입력 r과 출력 y의 단위를 일치시키기 위하여 스케일 계수 K₀를 포함하여 Fig. 4와 같이 전체 시스템 블록을 구성하였다. 실제 렌즈가 움직이는 변위는 블록선도에서 y에 해당하며, 홀센서에 의해 측정된 y_m와 차이가 있다. 본 연구에서는 관측되지는 않으나, 센서 모델을 기반으로 y를 추정하고, 이를 제어하는 것을 목표로 한다.

Fig. 4

Rescaled system block diagram

3. 제어 알고리즘 설계 및 성능 예측

3.1 시스템 평가지표

액추에이터의 제어 성능을 평가하기 위해서는 지표가 필요하다. 2절의 블록선도로부터 강인 안정성과 추종 성능을 평가하는 지표를 선정하였다. 블록 선도의 폐루프 전달함수는 식 (3)과 같이 나타낼 수 있고, 오차에 대한 전달함수는 식 (4)와 같다.

$\[ Y\left(s\right)=\begin{array}{l}\frac{C\left(s\right)G\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}R\left(s\right)\\ +\frac{G\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}D\left(s\right)\\ -\frac{C\left(s\right)G\left(s\right)H\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}N\left(s\right)\end{array} \]$

(3)

$\[ E\left(s\right)=\begin{array}{l}=R\left(s\right)-Y\left(s\right)\\ \frac{1+C\left(s\right)G\left(s\right)H\left(s\right)-C\left(s\right)G\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}R\left(s\right)\\ -\frac{G\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}D\left(s\right)\\ +\frac{C\left(s\right)G\left(s\right)H\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}N\left(s\right)\end{array} \]$

(4)

이를 이용한 평가지표에는 루프 함수(loop transfer function) L(s)를 이용하는 방법과 감도함수(sensitivity transfer function) S(s), 상보감도함수(complementary sensitivity transfer function) T(s)를 이용하는 방법이 있다^[12].

루프함수는 전통적으로 많이 이용하는 성능지표이고, 식 (5)와 같이 주어진다.

$\[ L\left(s\right)=C\left(s\right)G\left(s\right)H\left(s\right) \]$

(5)

만약, 센서 전달함수 H(s)를 1이라 가정하면 루프함수의 이득이 최대가 될 경우 식 (4)에서 추종입력 r으로부터 오차 e의 전달함수가 0으로 수렴하므로, 루프함수의 이득이 커질수록 시스템의 추종 성능이 좋다고 할 수 있다. 또한, 상대 안정성을 루프함수로부터 계산하므로 루프함수의 이득여유(gain margin)와 위상여유(phase margin)가 클수록 강인한 시스템이라 볼 수 있다.

폐루프 감도함수와 상보감도함수를 이용한 성능지표는 현대제어에서 일반적으로 이용되는 지표로 식 (6)과 같다.

$\[ \begin{array}{l}S\left(s\right)=\frac{1}{1+C\left(s\right)G\left(s\right)H\left(s\right)}\\ T\left(s\right)=1-S\left(s\right)=\frac{C\left(s\right)G\left(s\right)H\left(s\right)}{1+C\left(s\right)G\left(s\right)H\left(s\right)}\end{array} \]$

(6)

기존 현장에서는 주로 개루프 함수를 이용하여 성능을 평가한다. 그러나, 현대 제어공학에서는 주로 폐루프 함수를 이용하여 피드백 성능을 평가하기도 하고, H-infinity 방법^[15-16] 등 많은 알고리즘은 폐루프 함수를 목적함수로 이용하므로, 본 연구에서는 감도함수와 상보감도함수도 이용할 수 있도록 하였다. 식 (3), (4)에서 상보감도함수와 감도함수는 각각 입력으로부터 출력으로의 전달함수, 입력으로부터 오차로의 전달함수를 나타내기 때문에 상보감도함수가 1에 가까울수록, 감도함수가 0에 가까울수록 시스템은 좋은 추종성능을 가지게 된다. 또한, 감도함수의 상한 놈(norm)의 역수는 나이퀴스트(Nyquist) 선도에서 임계점과 루프 함수의 최단거리가 되기 때문에 상한 노름이 작을수록 시스템은 강인하다고 할 수 있다. 본 연구에서의 성능지표를 정리하면 Table 1과 같다.

Table 1

Performance evaluation index

Table 1에서 S_er(s)는 식 (4)에서 추종입력 r에서 렌즈 변위 y로의 전달함수를 해당한다. Table 1의 루프 함수를 이용한 지표는 기존 현업에서 타업체와 공통적으로 사용하는 지표이고, 아래는 현대 제어 관점에서 정확하다고 인지하는 지표이다.

3.2 PID 제어기 설계

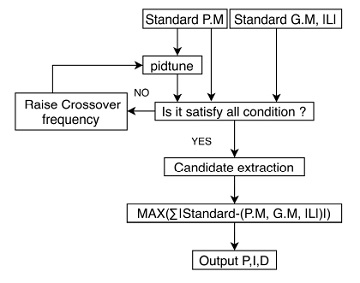
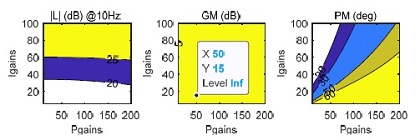
PID 제어의 이득을 정하는 가이드로는 특정 입력에 대한 응답의 기울기 등을 이용하는 Ziegler-Nichols 방법^[13] 등이 있지만, 설계 엔지니어도 수월하게 사용할 수 있도록 자동으로 게인을 찾아주는 알고리즘을 작성하였다. MATLAB에서 제공하는 pidtune 함수^[14]를 이용하여 플랜트의 동특성을 기반으로 교차 주파수(루프 대역폭)를 선택하고 사용자가 입력한 위상 여유를 목표로 PID 이득의 초기값을 선정한다. pidtune 함수는 성능 지표 중 위상 여유만을 고려하므로, 요구하는 루프 이득과 위상 여유를 만족하지 않을 수 있다. 따라서 pidtune에서 얻은 PID 이득을 기준으로 루프함수의 루프이득, 이득여유, 위상여유를 계산하여 최적이 되는 PI 이득을 자동으로 선정하게 된다. 해당 알고리즘의 순서도는 Fig. 5와 같으며, PID이득의 검토 범위, 루프이득, 이득여유, 위상여유의 조합으로구성된 목적함수에 대한 가중치 등을 사용자가 설정할 수 있도록 구성하였다. 또한, 사용자가 PID 이득을 직접 수정할 경우를 대비하여, 알고리즘에서 계산된 PID 이득과 인접한 PID 이득에 대한 루프이득, 이득여유, 위상여유를 Fig. 6과 같이 등고선으로 표현하였다.

Fig. 5

Flowchart of PID gain setting algorithm

Fig. 6

PI controller performance contour

3.3 H-infinity 제어기 설계

H-infinity 방법^[15-16]은 목적함수를 선정하면 수학적 최적화를 통해 최적의 제어기를 산출하는 방법으로, 원하는 성능에 대한 목적함수를 정하면 간단하게 제어기를 설계할 수 있다.

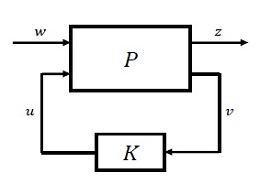
제어 시스템을 일반화하여 표현하면 Fig. 7과 같다. P는 일반화된 플랜트로 시스템 입력과 외란을 포함하는 외부입력 w와 조작변수 u를 입력으로 가지고 측정변수 v와 오차신호 z를 출력으로 가진다. 이를 식으로 표현하면 식 (7)과 같다.

$\[ \begin{array}{l}\left[\begin{array}{c}z\\ \upsilon \end{array}\right]=P\left(s\right) \left[\begin{array}{c}w\\ u\end{array}\right]=\left[\begin{array}{cc}{P}_{11}\left(s\right)& P_{12}\left(s\right)\\ P_{21}\left(s\right)& P_{22}\left(s\right)\end{array}\right] \left[\begin{array}{c}w\\ u\end{array}\right]\\ u=K\left(s\right)\upsilon \end{array} \]$

(7)

Fig. 7

General control configuration

오차신호 z와 외부입력 w의 관계는 식 (8)과 같이 표현되고, 이의 H-infinity 놈을 목적함수로 하여 최소가 되게 하는 제어기 K 를 산출하게 된다.

$\[ \begin{array}{l}z=F_l\left(P,K\right)w\\ F_l=\left(P,K\right)=P_{11}+P_{21}K{\left(I-P_{22}K\right)}^{-1}{P}_{21}\end{array} \]$

(8)

본 연구에서는 성능지표에 대해 최적화된 제어기를 설계할 수 있도록 식 (9)와 같이 감도함수와 상보감도함수에 대한 목적함수를 이용하였다.

$\[ J={‖F_l\left(P,K\right)‖}_{\infty }={‖\left[\begin{array}{c}{W}_{1}S\\ W_{2}T\end{array}\right]‖}_{\infty } \]$

(9)

최종적으로 W₁과 W₂을 형태를 구성하면 의도하는 감도함수와 상보감도함수를 얻을 수 있다. 이 방법은 기존의 논문에서 자세히 설명되어 있다^[6].

4. 폐루프 측정을 통한 제어 성능평가

4.2 폐루프 전달 함수의 측정

Fig. 8는 제어기 구현 검증을 위하여 폐루프 측정 과정에서 신호의 측정점을 나타낸다. 측정은 설정한 주파수 범위 내에서 sine sweeping을 통해 이루어지며, 각 측정 신호에 대한 주파수 응답으로 식 (2)-(5)로부터 루프함수, 감도함수, 상보감도함수를 추정하고, 성능지표에 대해 비교할 수 있다.

Fig. 8

Signals measured in closed loop experiment

5. 실험 및 검증

2~4절까지의 내용을 바탕으로 실제 OIS 액츄에이터에 대하여 제어기 설계 및 실험을 진행하였다.

먼저, Fig. 8의 시스템에서 제어입력 u와 측정값 y를 이용하여 직접 주파수 응답을 측정하였다. 시제는 개발단계의 임의의 OIS 액추에이터 시제를 이용하였다. 본 연구에서 사용한 볼 스테이지 기구는 마찰력이 존재하는 데 전력 소비를 줄이기 위하여 낮은 전류를 사용하므로 저진폭에서 움직임이 부족한 경우가 발생할 수 있기 때문에, 먼저 정현파의 진폭을 다르게 해가면서 출력 진폭을 확인하였고 이를 통해 선형성을 점검하였다.

본격적인 주파수 응답에서는 수 Hz부터 최대 3 kHz까지 정현파를 발생시키고 나오는 측정값을 FFT를 통해 주파수 응답을 구하였다. 이때 AF (auto focus) 기능을 켜거나 끄고 테스트하여 특성 변화를 살펴보았고. 여러 개의 측정 데이터를 얻어서 전달함수 추정을 위한 공칭 응답을 계산하였다.

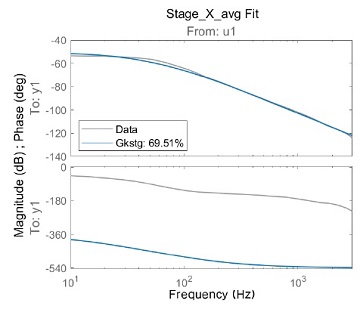
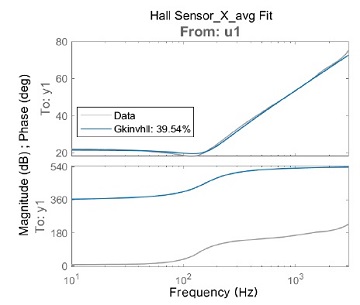
개루프 측정 결과로부터 계산한 공칭 응답을 이용하여 전달함수를 추정하였다. 전달함수 추정을 위해 주파수의 상한을 정하고 주파수에 대한 가중치 필터를 정하였고 이를 통해 안정적인 영역에서의 전달함수를 계산하였다. Figs. 9, 10은 시제의 홀센서, 레이저 변위계 측정결과의 공칭응답에 대한 전달함수 추정결과를 나타낸다.

Fig. 9

Actuator identification result

Fig. 10

Hall sensor identification result

전체 평가시스템 중 제어기 설계파트는 2.3절에서 언급한 inverse 필터와 notch 필터의 사용 여부와 파라미터값을 지정하고 PI, hinf, lead-Llg 또는 custom (외부에서 설계한 설계 파라미터 입력) 등의 제어기를 선택하여 설계하여 3.1절의 성능지표에 대해 분석하게 구성하였는데, PID 제어의 경우 3.2절의 PID 제어기 설계 알고리즘을 통해서 요구하는 성능지표에 대해 자동으로 PID 이득을 찾을 수 있다. 제어기 설계 파트는 모듈화하여, 차후 다른 제어 방법을 새롭게 추가하고, 확장이 가능하도록 설계되었다. 이를 이용하여 PID 제어기를 선택, 추정된 홀센서와 레이저 변위계의 전달함수를 바탕으로 Table 2의 목표성능에 맞는 적절한 PID 이득을 선정하였다.

Table 2

Experimental performance objectives

설계된 제어기를 이용하여 폐루프 측정을 하기 위해 4.1 절의 이산화 방법을 통해 제어기를 이산화하고 이산화된 제어기를 마이크로컨트롤러에 명령문 형태로 저장하였다. 그리고, Table 3과 같이 정현파의 주파수 범위, 크기 등의 실험조건을 설정한 뒤 Fig. 8에 나타난 4가지 신호를 측정하여 이로부터 제어기의 성능을 평가하였다.

Table 3

Closed loop measuring condition

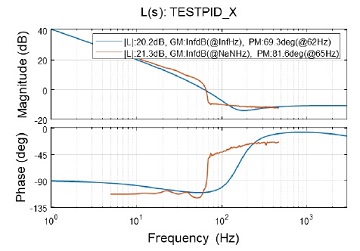
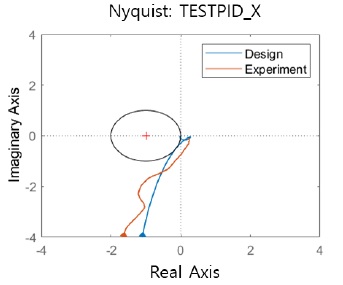
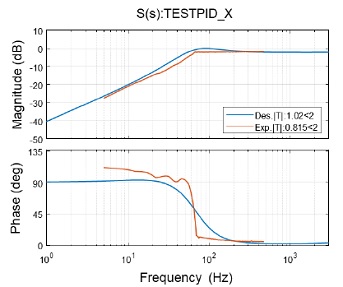
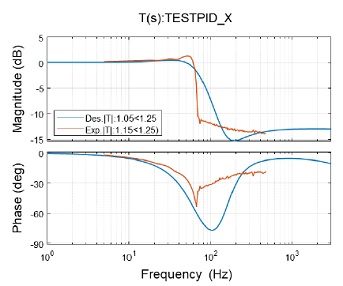
Figs. 11~14는 해석적인 식별 모델과 제어기 모델을 이용한 전달 함수와 폐루프 측정으로부터 계산한 전달 함수를 비교한 결과이다. 비교결과 해당 시제는 Table 4와 같이 목표 성능 기준을 모두 만족하는 것을 확인하였고. 설계된 제어기와 측정된 제어기가 비슷한 결과를 보임을 확인하였다. 이를 통해 본 연구에서 개발한 시스템을 이용한 시제의 성능평가가 가능함을 확인하였다.

Fig. 11

Loop transfer function L

Fig. 12

Nyquist plot

Fig. 13

Sensitivity transfer function S

Fig. 14

Complementary transfer function T

Table 4

Comparison of design and measured objective values

6. GUI 프로그램 구성

액추에이터 평가 시스템의 GUI 프로그램은 MATLAB 앱디자이너^[18]를 사용하여 별도의 프로그램으로 제작하였기 때문에 MATLAB 라이센스가 없이도 사용할 수 있다.

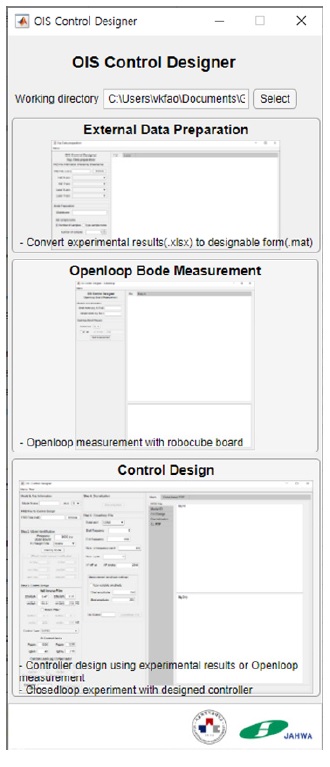
GUI 구성은 Fig. 15와 같이 외부에서 측정된 실험데이터를 확인하고, 제어설계프로그램에서 사용할 수 있는 형태로 변환하는 external data preparation, 개루프 주파수 응답을 측정할 수 있는 openloop bode measurement, 2~4절까지의 과정으로 컨트롤러 설계 및 성능실험을 진행하는 control design으로 구성하였으며, 5장의 모든 실험 과정을 GUI를 통해 진행할 수 있도록 하였다.

Fig. 15

OIS control designer

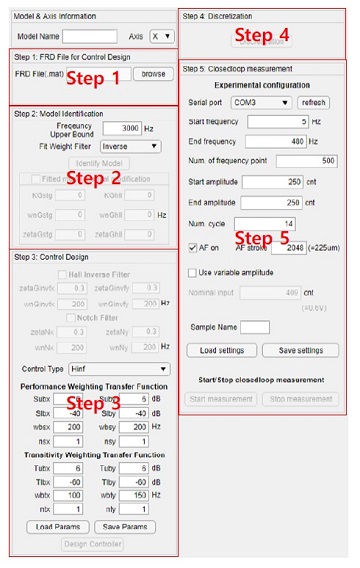
Fig. 16은 GUI 프로그램 중 가장 주가 되는 부분인 control design 파트의 파라미터 입력부를 나타낸다. step 1~5까지로 나뉘며 step 1은 주파수 응답함수를 불러오는 부분이며, step 2~4는 각각 2~4.1절, step 5는 4.2절의 구성과 부합하도록 구성하였다.

Fig. 16

Control design panel

7. 결 론

본 논문에서는 OIS 액추에이터의 성능 평가를 위하여, 복잡한 구성없이 독립적인 환경에서 설계 엔지니어가 제어기를 직접 설계, 평가할 수 있는 평가 시스템을 구축하였다. 구축된 시스템을 이용하여, 제어기를 설계하고 평가한 결과 목표성능을 만족하는 제어기를 설계할 수 있음을 확인하였고, 이를 통해 본 논문의 평가 시스템만을 이용하여 OIS 액추에이터의 성능평가가 가능함을 확인하였다. 또한, PI, H-infinity 등의 제어기 설계파트를 모듈화 하여 제어이론에 기반한 새로운 알고리즘 추가 등으로 다양한 방향의 확장이 가능하도록 하였다. 본 시스템을 통하여 액추에이터 개발 업체는 개발한 시제품을 자체적으로 테스트해보고, 이에 따라 기구 구성을 재검토할 수 있게 되었다. 이를 통해, 액추에이터를 개발하고 예상되는 최대 제어 성능을 예측할 수 있으며, 불필요한 제어기 업체와의 의뢰 검토 과정을 줄임으로써, 개발 기간을 단축시키는 효과를 얻을 수 있었다.

Acknowledgments

이 연구는 2020년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0008473, 2020년 산업혁신인재성장지원사업).

References

• Galastian, T. V., 2013, Smart Mini-Cameras, CRC Press, USA. [https://doi.org/10.1201/b15555]
• La Rosa, F., Virzi, M. C., Bonaccorso, F., Branciforte, M., viewed 13 November 2019, Optical Image Stabilization (OIS) White Paper, ver.1.2, STMicroelectronics, <https://www.st.com/resource/en/white_paper/ois_white_paper.pdf, >.
• ROHM Semiconductor, viewed 15 May 2020, Optical Image St abilization (OIS), <https://www.rohm.com/documents/11303/41217/OIS-white-paper.pdf, >.
• Chiu, C.-W., Chao, P.C.-P., Wu, D.-Y., 2007, Optimal Design of Magnetically Actuated Optical Image Stabilizer Mechanism for Cameras in Mobile Phones via Genetic Algorithm, IEEE Trans. Magnet., 43:6 2582-2584. [https://doi.org/10.1109/TMAG.2007.893320]
• Chao, P.C.-P., Chen, Y.-H., Chiu, C.-W., Tsai, M.-Y., Chang, I.-Y., Lin, S.-K., 2011, A New Two-DOF Rotational Optical Image Stabilizer, Microsyst. Technol., 17 1037-1049. [https://doi.org/10.1007/s00542-011-1288-9]
• Lee, C., 2014, H∞ Control on the Optical Image Stabilizer Mechanism in Mobile Phone Cameras, Journal of the Korean Society of Manufacturing Technology Engineers, 23:3 266-272. [https://doi.org/10.7735/ksmte.2014.23.3.266]
• Wang, J. H.-S., Qiu, K. F., Chao, P. C. P., 2017, Control Design and Digital Implementation of a Fast 2-Degree-of-Freedom Translational Optical Image Stabilizer for Image Sensors in Mobile Camera Phones, Sensors, 17:10 2333. [https://doi.org/10.3390/s17102333]
• Lee, S. K., Kong, J. H., 2018, A Study on the Design Exploration of Optical Image Stabilization (OIS) for Smart Phone, Journal of Digital Contents Society, 19:8 1603-1615. [https://doi.org/10.9728/dcs.2018.19.8.1603]
• Lee, C., Cha, S. H., Kim Y. S., 2015, Identification and Control Design of Voice Coil Actuated Stabilization, Optical Image System, Proceedings of the 6th International Conference on Manufacturing, Machine Design and Tribology.
• Ozdemir, A. A., Gumussoy, S., 2017, Transfer Function Estimation in System Identification Toolbox via Vector Fitting, IFAC PapersOnLine, 50:1 6232-6237. [https://doi.org/10.1016/j.ifacol.2017.08.1026]
• Mathworks, viewed 15 November 2019, tfest, <https://www.mathworks.com/help/ident/ref/tfest.html, >.
• Franklin, G. F., Powell, J. D., Emami-Naeini, A., 2019, Feedback Control of Dynamic Systems, PennWell, Japan.
• Ziegler, J. G., Nichols, N. B., 1993, Optimum Settings for Automatic Controllers, Journal of Dynamic Systems, Measurement, and Control., 115:2B 220-222. [https://doi.org/10.1115/1.2899060]
• Mathworks, viewed 17 November 2019, pidtune, <https://www.mathworks.com/help/control/ref/pidtune.html, >.
• Doyle, J. C., Glover, K., Khargonekar, P., Francis, B., 1989, State-space Solutions to Standard H2 and H∞ Control Problems, IEEE Transactions on Automatic Control, 34:8 831-847. [https://doi.org/10.1109/9.29425]
• Skogestad, S., Postlethwaite, I., 2005, Multivariable Feedback Control: Analysis and Design, Wiley, New York.
• Mutambara, A. G. O., 1999, Design and Analysis of Control Systems, CRC Press, Boca Raton, Florida.
• Mathworks, viewed 10 February 2020, MATLAB App Designer, <https://www.mathworks.com/products/matlab/app-designer.html, >.