비선형 접촉을 고려한 대면적 롤투롤 가압 공정의 접촉 압력 분포 해석

1. 서 론

현대 사회에 이르러 지구 온난화와 같은 기후 재앙 문제가 대두되면서 자동차 시장에 대한 국제적인 환경 규제가 강화되고 있다. 환경 규제가 강화되면서 자동차 시장의 패러다임도 기존의 내연기관 중심에서 전기 자동차로 빠르게 변화하고 있으며, 전기 자동차에 대한 기술 수요도 함께 증가하고 있다. 전기 자동차의 핵심 기술은 이차 전지 기술로 리튬 이온 배터리가 대표적이며, 재충전이 가능하여 친환경 및 경제적이면서 배터리의 에너지 밀도가 높은 장점을 가지고 있다^[1].

이러한 이차 전지는 롤투롤(roll-to-roll) 공정을 기반으로 생산되며, 롤투롤 공정은 저비용 대량생산에 적합하다는 장점을 가진다^[2]. 이차 전지 제작 공정의 구성은 주재료인 음극재와 양극재를 슬러리(slurry) 형태로 혼합하는 믹싱(mixing) 공정, 믹싱된 슬러리를 Cu, Al 박판에 얇게 도포하여 건조시키는 코팅(coating) 공정, 두 개의 압연 롤 사이로 전극을 통과시키면서 압축시키는 롤-프레싱(roll-pressing) 공정, 배터리 규격에 맞게 전극 폭을 재단하는 슬리팅(slitting) 공정 및 불필요한 부분을 제거하는 노칭(notching) 공정 순으로 진행된다. 이차 전지의 효율을 의미하는 에너지 밀도는 단위 부피당 저장된 에너지 양을 의미하며, 이차 전지의 에너지 밀도를 증가시키기 위해서는 롤-프레싱 공정에서 전극 두께의 압축률을 증가시켜야 한다. 또한 균일한 품질의 이차 전지 생산을 위해서는 롤-프레싱 공정에서 롤 축 방향으로 균일한 가압력 분포가 필요하다. 하지만 가압 과정에서 롤러의 소성 변형을 방지하기 위해 코팅된 고무층의 미소 접촉 변형, 가압 롤 축 간의 정렬 오차, 롤의 굽힘 변형 등으로 불균일한 가압력 분포가 발생하게 된다^[3].

롤투롤 가압 공정에서 발생하는 불균일한 압력 분포와 관련된 선행 연구는 지속적으로 진행되었다. Hertz는 매끄러운 곡면의 구나 원통 형상의 탄성체가 점 또는 선 접촉을 할 때, 접촉 면적에서 발생하는 응력 분포를 이론적으로 설명하였다^[4-5]. D. R. Roisum은 롤투롤 가압 시스템에서 접촉 압력의 불균일한 분포를 야기하는 가장 큰 요인은 롤의 굽힘 변형이라고 설명하였으며, 롤의 직경 대비 길이가 길어지거나, 가압 하중이 커질수록 압력 분포의 편차가 커진다고 설명하였다^[6]. J. W. Kannel 등은 롤 가압 시스템의 축이 평행하지 않을 때, 롤의 축 정렬 오차로 인해 발생하는 불균일한 응력 분포가 롤과 롤 베어링의 피로 수명에 미치는 영향을 실험을 통하여 제시하였다^[7]. K. C. Hinge 등은 롤의 축 정렬 오차와 접촉 압력 분포 사이의 관계를 나타내는 수학적 모델을 제안하고, 길이 350 mm의 롤 가압 시스템에서 축 정렬 오차로 인해 발생하는 접촉 압력 분포 실험 결과를 제시하였다^[8]. Z. Ye 등은 롤 가압 공정에서 롤 베어링의 편심과 접촉 압력 분포 사이의 관계를 나타내는 수학적 모델을 제안하고, 롤에 crown 형상을 적용한 접촉 압력 분포를 유한요소해석을 통하여 제시하였다^[9]. R. Servin 등은 롤 가압 공정에서 가압 롤과 지지 롤의 Positive-crown 혹은 Negative-crown 형상의 조합에 따라 롤에 발생하는 응력 분포와 접촉 압력 분포의 결과를 유한요소해석을 통하여 제시하였다^[10]. Kim 등은 1,400 mm 롤투롤 가압 공정의 접촉 압력 분포를 측정하고, 불균일한 가압력 분포를 보정하기 위한 다중 롤러 기구를 제안하였다^[11].

본 연구에서는 비선형 접촉 조건을 고려하여 1,400 mm 폭의 대면적 롤투롤 가압 시스템에서 접촉면에 발생하는 응력 분포를 유한요소해석을 통하여 분석하였다. 대면적의 가압 공정을 위해 롤러의 길이가 증가하면, 롤러의 굽힘 변형이 증가하여 가압 롤과 지지 롤 사이의 접촉면에서 비선형 접촉이 발생한다. 접촉 상태에서 비접촉 상태 혹은 비접촉 상태에서 접촉 상태로 접촉 조건이 변화하는 비선형 접촉을 고려하기 위한 롤투롤 가압 시스템의 해석 모델링을 진행하고, 좌우 1,000 N의 하중으로 1 mm 변위 가압하는 조건에서 발생하는 접촉면의 압력 분포를 확인하였다.

2. 롤투롤 가압 시스템의 유한요소해석

2.1 롤투롤 가압 시스템 비선형 접촉 해석 모델링

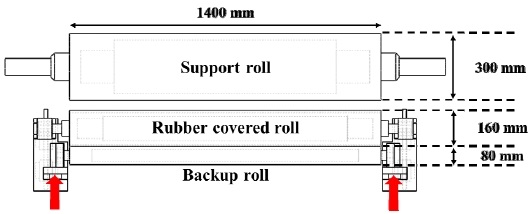
대면적 롤투롤 가압 공정의 유한요소해석을 위한 해석 모델링을 진행하였다. 유한요소해석은 상용 소프트웨어 ANSYS를 사용하였다. 해석 모델은 이차 전지의 대면적 생산을 위한 1,400 mm 롤투롤 가압 시스템으로 지지 롤과 고무 롤, 백업롤로 구성되어 있다. 고무 롤은 선형 가이드 위에 지지되어 있으며, 가압 시 백업 롤을 통해 고무 롤에 분포 하중이 전달되도록 시스템이 구성되어 있다. Fig. 1은 1,400 mm 롤투롤 가압 시스템의 개략도를 나타낸 것이다. 지지 롤, 고무 롤, 백업 롤의 길이는 1,400 mm로 동일하고, 지지 롤의 직경은 300 mm, 고무 롤의 직경은 160 mm, 백업 롤의 직경은 80 mm이다. 롤의 재질은 Al으로 설정하였고, 선형 가이드 및 롤 베어링을 포함하는 기타 부속품은 스테인리스 스틸로 설정하였다.

Fig. 1

Schematic of a roll-to-roll pressing system

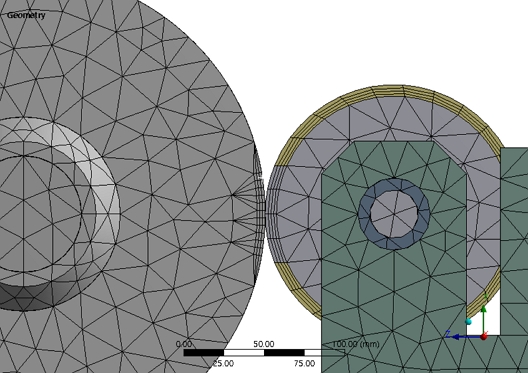
롤 가압 시 고무 롤에서 발생하는 변형은 미소하다고 가정하여, 고무의 물성은 선형 물성치로 적용하였다. 유한요소해석에 사용한 재료의 기계적 물성치는 Table 1에 나타내었다. 전체 시스템 모델의 격자 크기는 20 mm로 설정하였고, 지지 롤과 고무 롤 사이의 접촉 영역은 Fig. 2와 같이 반경 방향으로 여러 층의 격자를 가지도록 Fine 하게 설정하였다. 롤러의 길이 방향은 10 mm 간격으로 140개의 절점을 가지도록 격자를 생성하였다.

Table 1

Mechanical properties for finite element analysis

Fig. 2

The mesh shape of contact surface between the support and rubber covered roll

2.2 경계조건

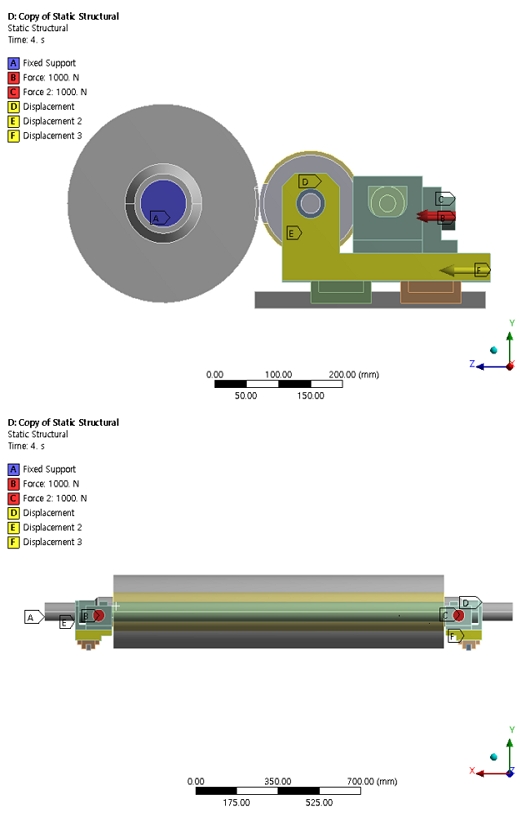
Fig. 3은 유한요소해석의 경계 조건을 나타낸 것이다. 가압 롤러의 회전은 발생하지 않는 준정적 상태를 고려하여 지지 롤과 고무 롤 사이의 접촉면에서 마찰은 발생하지 않는다고 가정하였다. 지지 롤의 양 끝단과 선형 가이드 레일의 바닥 면은 고정단(fixed support)으로 모든 자유도를 구속하였다.

Fig. 3

Boundary conditions for roll-to-roll pressurization systems

선형 가이드 레일과 블록 사이의 접촉 조건은 No separation으로 마찰 없이 이동하지만, 접촉면에 수직 방향으로는 변위가 발생하지 않도록 선형 접촉 조건을 설정하였다. 지지 롤과 고무 롤 사이의 접촉은 Frictionless로 마찰은 없고, 가압 되면서 접촉 상태가 비접촉에서 접촉으로 변화되도록 비선형 접촉 조건을 설정하였다. 추가로 선형 가이드 더미 블록 옆면에 가압 방향 자유도를 제외하고 나머지 자유도를 구속하였다. 가압 조건은 가압 방향으로 변위 1 mm, 선형 가이드의 좌우에 1,000 N으로 총 2,000 N의 하중이 작용하도록 설정하였다. 비선형 접촉의 해석 수렴성을 증가시키기 위해 하중 조건을 Table 2와 같이 4단계로 나누어서 적용하였다.

Table 2

Load steps applied to increase the convergence of analysis results

3. 롤투롤 가압 시스템의 접촉 압력 분포

3.1 유한요소해석의 수렴성 검토

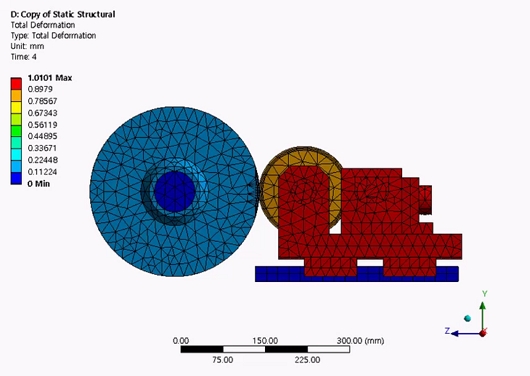
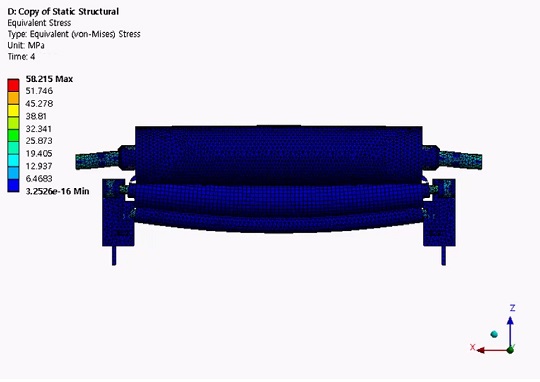
Fig. 4에 하중단계에 따라 접촉이 발생한 절점의 개수를 나타내었다. 초기 간격이 있는 상태에서 하중단계 1에 해당하는 0.1 mm 가압 변위까지는 접촉을 인식하지 못하고, 0.2 mm 가압하는 하중단계 2부터 접촉면의 140개 절점이 접촉을 인식하였다. Fig. 5는 지지 롤과 고무 롤 사이 끝단 절점의 하중단계에 따른 가압 방향 변형량을 나타낸다. 하중단계 1에서는 접촉을 인식하지 못하였기 때문에, 가압 변위에 해당하는 0.1 mm의 변형량이 발생하였고, 접촉을 인식한 하중단계 2부터는 가압 변위 0.2 mm 보다 적은 변형량이 발생하였다. 최종적으로 1 mm 변위를 가압하는 하중단계 4에서의 가압 방향변형량은 대략 0.53 mm이다. 이는 고무 롤이 가압 방향으로 압축되면서 가압 변위보다 적은 변형량이 발생한 것이다. Fig. 6은 최종 하중단계까지 진행된 이후, 전체 시스템의 변형량을 나타낸 것이다. Fig. 7은 최종 하중단계까지 진행된 이후 전체 시스템의 응력 분포를 100배 스케일로 나타낸 것이다. 1400 mm 롤투롤 가압 시스템에서 양 끝단에 1,000 N 및 1 mm 변위로 가압했을 때, 최대 58.22 MPa의 응력이 발생하였고, 가압력에 의한 롤러의 굽힘이 발생하는 것을 확인하였다.

Fig. 4

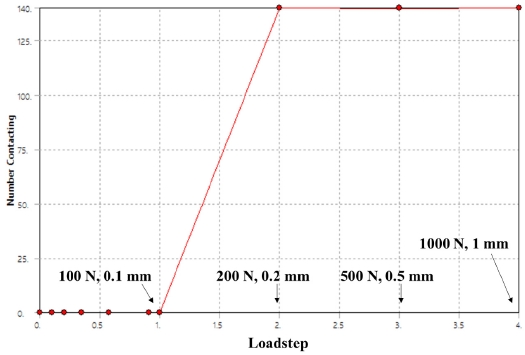
The number of contact nodes between the support roll and the rubber roll according to the load steps

Fig. 5

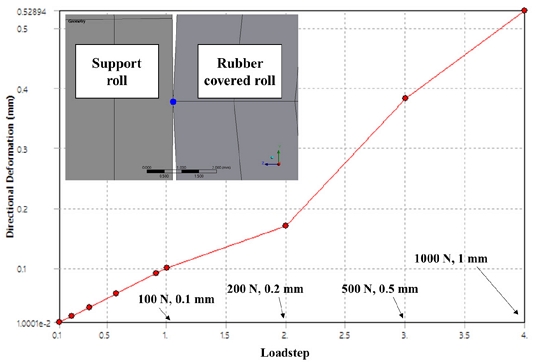
The directional deformation that occurs at the end node between the support roll and the rubber covered roll according to the load steps

Fig. 6

Total deformation of the entire system after the final load step

Fig. 7

After the final load step, the deformation pattern and stress distribution of the entire system (scale×100)

3.2 유한요소해석의 결과

롤투롤 가압 시스템은 롤의 길이가 길어질수록 롤의 굽힘에 의한 불균일한 가압력 분포가 발생한다. 본 연구에서는 1,400 mm 폭의 롤투롤 가압 시스템에서 발생하는 응력 분포를 유한요소해석을 통하여 분석하였다. 롤투롤 가압 시스템에서 고무 롤이 지지 롤을 총 2,000 N의 하중으로 1 mm 변위 가압할 때 지지 롤의 접촉면에서 발생하는 응력 분포를 Fig. 8에 나타내었다. 접촉면에서 발생하는 최대 14.85 MPa의 응력이 발생하였다. 1 mm 변위 가압하였을 때, 고무 롤의 접촉면에서 양 끝 단과 중심 사이의 불균일한 응력 분포를 확인할 수 있다. 또한, 롤의 중심축 방향으로 접촉 면적의 차이 및 롤 자체의 굽힘 변형에 의한 응력 분포를 확인할 수 있다. Fig. 9는 지지 롤과 고무 롤 사이 접촉면 중심축에서 발생하는 응력 분포를 나타낸 것이다. 접촉면의 중심축에서는 최대 11.7 MPa의 응력이 발생하였고, 최소로는 0.71 MPa의 응력이 발생하였다. 1,400 mm 롤투롤 가압 시스템에서 총 2,000 N의 하중으로 1 mm 변위 가압을 하였을 때, 대략 11 MPa의 응력 분포의 편차가 발생하는 것을 확인하였다.

Fig. 8

Stress distribution under pressure of total 2,000 N load and 1 mm displacement

Fig. 9

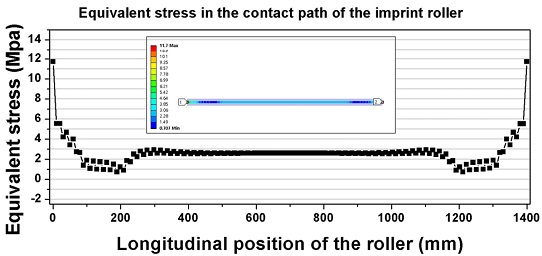
Stress distribution occurring in the contact path parallel to the central axis of the support roll and the rubber roll

1,400 mm 롤투롤 가압 공정의 압력 분포 측정 실험 결과는 Kim 등의 연구에서 제시되었다^[11]. Kim 등의 연구에서는 면압지를 이용하여 좌우 200 kgf으로 총 400 kgf 하중 조건에서 접촉면의 압력 분포를 측정하였다. 실험의 결과에서는 최대 압력이 2~2.5 MPa 범위에서 측정되었고, 최소 압력은 1~1.5 MPa 범위에서 측정되었으며, 대략 1 MPa의 가압력 분포 편차를 가진다. 유한요소해석과 실험의 결과 차이는 재료의 물성, 실험의 측정 오차, 측정 시스템의 조립 오차 등 여러 가지 요인이 작용한다. 특히 본 연구에서 해석 모델의 가압 변위를 1 mm로 가정한 것이 과도한 조건으로 추측된다. 그러나, 현실적으로 실제 가압 시스템의 롤러 축 사이 가압 변위는 확인이 어렵다. 실험 연구의 하중이 본 연구의 약 2배에 해당하고, 실제 롤러 축 사이의 상대 이동량도 경험적으로 볼 때, 본 연구의 1 mm의 20% 정도인 0.2 mm로 가정하는 것이 더 현실적이다. 이러한 조건들이 탄성 영역에서 선형적으로 반영된다고 가정하여 본 연구의 해석 결과에 대입하면, 응력 분포의 차이는 약 1.1 MPa로 유추할 수 있다. 그러므로, 이 연구에서 나타나는 압력 분포 편차의 경향성은 실제 시스템의 결과를 잘 반영한다고 할 수 있다.

따라서, 본 연구의 가압력 분포 해석 모델은 가압 실험의 결과와 같이 롤 양 끝단이 접촉하는 영역에서 응력 분포가 집중되는 경향을 잘 반영하고 있으며, 가압력 분포의 편차 보정을 위한 분석 모델로 활용할 수 있다.

4. 결 론

본 연구에서는 롤투롤 시스템 기반의 가압 공정에서 발생하는 불균일한 응력 분포를 유한요소해석을 통하여 분석하였다. 롤투롤 가압 공정에서 불균일한 응력 분포를 일으키는 원인에는 롤의 굽힘 변형, 가압 접촉면의 변형, 롤의 축 정렬 오차 등이 존재한다. 그중에서 롤의 굽힘 변형에 의한 응력 편차는 롤의 길이에 비례하여 크게 발생한다.

가압 공정에서 접촉면에 발생하는 응력 분포를 분석하기 위하여 1,400 mm 가압 시스템의 유한요소해석 모델링을 진행하였고, 가압 조건은 총 2,000 N의 하중으로 1 mm 가압하는 조건을 설정하였다. 1 mm 가압하는 조건에서 접촉 지점의 가압 변위는 0.53 mm가 발생하였고, 지지 롤 축과 가압 롤 축 사이의 접촉면에서의 응력 분포는 최대 11.7 MPa, 최소 0.71 MPa로 대략 11 MPa의 응력 분포 편차가 발생하는 것을 확인하였다.

본 연구에서 분석한 가압 롤러 사이의 응력분포 해석 결과는 실제 가압 상황에서 롤러 양 끝단에서 발생하는 굽힘 변형 및 롤러 접촉면에서 응력 분포가 집중되는 경향을 잘 반영하고 있다. 또한, 경향성이 실제 실험의 결과를 따르는 것으로 판단되어, 가압력 분포의 편차를 보정하기 위한 분석 모델로 활용할 수 있다.

Acknowledgments

본 연구는 2022년도 정부(산업통산자원부)의 재원으로 한국산업기술평가관리원의 지원을 받아 수행된 연구임. (No. 00155961, Flash 광원을 적용한 고효율 탄소저감형 고로딩 전극 건조 시스템 개발).

References

• Duffner, F., Kronemeyer, N., Tübke, J., Leker, J., Winter, M., Schmuch, R., 2021, Post-lithium-ion Battery Cell Production and its Compatibility with Lithium-ion Cell Production Infrastructure, Nat. Energy., 6:2 123-134.. [https://doi.org/10.1038/s41560-020-00748-8]
• Liu, Y., Zhang, R., Wang, J., Wang, Y., 2021, Current and Future Lithium-ion Battery Manufacturing, iScience, 24:4 102332. [https://doi.org/10.1016/j.isci.2021.102332]
• Roisum, D. R., 1998, The Mechanics of Web Handling, Tappi Press, USA.
• Johnson, K. L., 1987, Contact Mechanics, Cambridge university press., United Kingdom.
• Roisum, D. R., 1996, The Mechanics of rollers, Tappi Press, USA.
• Popov, V. L., 2010 Contact Mechanics and Friction, Springer, Germany. [https://doi.org/10.1007/978-3-642-10803-7]
• Kannel, J., Hartnett, M., 1983, Theoretical and Experimental Evaluation of Edge Stresses Under Severe Edge Loads, ASLE Transactions, 26:1 25-30. [https://doi.org/10.1080/05698198308981473]
• Hinge, K., Maniatty, A., 1996, The Effect of Skew Angle on the Axial Pressure Distribution between Flexible Rubber-covered Rollers, Int. J. Mech. Sci., 38:6 607-619. [https://doi.org/10.1016/S0020-7403(96)80004-X]
• Ye, Z., Wang, L., Gu, L., Zhang, C., 2013, Effects of Tilted Misalignment on Loading Characteristics of Cylindrical Roller Bearings, Mech. Mach. Theory, 69 153-167. [https://doi.org/10.1016/j.mechmachtheory.2013.05.006]
• Servin, R., Arreola, S. A., Calderón, I., Perez, A., San Miguel, S. M., 2019, Effect of Crown Shape of Rolls on the Distribution of Stress and Elastic Deformation for Rolling Processes, Metals, 9:11 1222. [https://doi.org/10.3390/met9111222]
• Kim, G. E., Kim, H., Woo, K., Kang, Y., Lee, S., Jeon, Y., Lee, M. G., Kwon, S., 2021, Uniform Pressing Mechanism in Large-Area Roll-to-Roll, Nanoimprint Lithography Process, Appl. Sci.-Basel, 11:20 9571. [https://doi.org/10.3390/app11209571]