사출금형용 직선형 냉각회로의 정량적 설계 방법론 개발

1. 서 론

사출성형은 용융 상태인 고온의 수지를 금형에 주입하여 냉각시킨 후 제품을 취출하는 공정이며 일반적으로 냉각시간이 제품 총 생산 시간의 50% 이상을 차지하므로 제품 생산 시간을 단축시키기 위해서는 냉각시간을 단축시키는 것이 가장 효율적인 방법이다.

이러한 사출성형의 냉각공정은 금형에 설치된 냉각관에 의해 수행되며 기존엔 건드릴을 이용한 기계 가공이 유일한 냉각관 가공 방법이었기에 직선형 냉각관의 배치를 최적화하여 냉각효율을 개선시키는 연구가 많이 수행되었다^[1-3]. 그러나 본 연구는 형상적응형 냉각회로의 개념이 등장하면서^[4] 중단되었으며 최근엔 형상적응형 냉각회로의 효율을 개선시키기 위한 연구와^[5-7] 기계학습을 이용한 형상적응형 냉각회로의 효율적 설계^[8] 등의 연구가 주를 이루고 있다.

형상적응형 냉각회로란 3D 프린터를 이용 제품 표면을 따라가면서 냉각관이 설치되는 방식으로 제품 형상에 제약 받지 않아 냉각효율을 극대화시킬 수 있다는 장점이 있다. 그러나 가장 큰 단점은 기존의 기계가공 대비 제작 일정 및 제작 단가가 수십 배 이상 차이가 발생해서 양산 공정에 적용하기 어렵다는 것이다.

특히나 국내 금형산업은 회사의 연간 매출이 5억 미만의 소기업인 경우가 국내 전체 회사의 약 55%를 차지하고 있으며 대기업에서 일감을 수주해서 금형을 제작 후 납품하는 형태의 수주형 업무를 담당하므로 연구개발 진행 및 신기술 적용 자체가 힘든 상황이다^[9].

오히려 수주형 업무의 특성상 고객의 다양한 설계변경에 빠르게 대응해 금형설계 일정을 단축시킬 수 있는 방법을 선호하는데 기존에 제시된 연구들은 모두 현실적인 조건인 시간에 대한 고려가 빠졌다. 특히나 선행 연구에서 공통적으로 등장하는 내용 중 하나인 해석프로그램의 사용은 가격적인 문제로 특정 대기업을 제외한 대부분의 기업체에선 사용하지 못한다.

본 연구에서는 전술한 현실적 문제점인 시간과 비용을 고려한 직선형 냉각회로의 정량적 설계 방법론을 제안하고자 한다. 고객사의 다양한 설계변경에 빠르게 대응할 수 있어야 하며 별도의 해석프로그램을 사용하지 않아도 활용할 수 있는 방법론의 개발에 중점을 두었다.

먼저, Xu^[10]의 연구 결과에 제안된 금형표면온도를 예측하는 수식을 기반으로 냉각관의 직경, 깊이, 간격의 관계식을 유도하였다. Xu는 금형에서 발생되는 열전달 문제를 2차원 평면상으로 단순화시킨 후 관계식을 정리했는데 본 연구에서는 이를 기반으로 중요도가 낮은 변수를 제거하고 냉각관의 깊이와 간격을 변수로 하는 수식을 유도해 최종적으로 냉각회로 설계용 그래프를 작성할 수 있도록 만들었다.

본 그래프는 사출성형 공정 중 많이 활용되는 열가소성 소재 중 PP(polypropylene), ABS(acrylonitrilebutadienestyrene), PC(polycarbonate), PMMA(polymethylmethacrylate)의 물성 값을 이용하여 계산 후 그 값의 타당성을 검토하였다. 마지막으로 실제 PP를 이용 생산되는 자동차 범퍼 제품에 설계 그래프를 적용하여 냉각회로를 제작한 후 Autodesk사의 사출성형해석 프로그램인 Moldflow Synergy 2021를 이용 냉각해석까지 수행하여 그 효과를 확인하였다.

2. 본 론

2.1 금형 내부에서의 열전달 과정

사출성형 공정은 일반적으로 충진/보압/냉각/취출의 4단계로 이루어져 있다고 알려져 있지만 냉각 공정은 고온의 용융 수지가 금형 벽면에 닿는 즉시 냉각이 진행되므로 소재의 관점에서 본다면 충진과 동시에 냉각이 진행된다고 볼 수 있다. 이 때 용융 수지가 가지고 오는 열량은 금형에 일부 전달되고 남은 열량은 냉각수가 모두 제거된다고 가정하면 냉각이 종료된 후 금형표면의 온도는 다음과 같은 수식 (1)로 나타낼 수 있다^[10].

$\[ {\overline{T}}_m=T_c+\frac{{\rho }_p{C}_p{l}_p\left(2K_{m}W+h\pi D{l}_m\right)\left(T_{\text{melt}}{\text{-T}}_{\text{eject}}\right)}{h\pi D{K}_m{t}_c} \]$

(1)

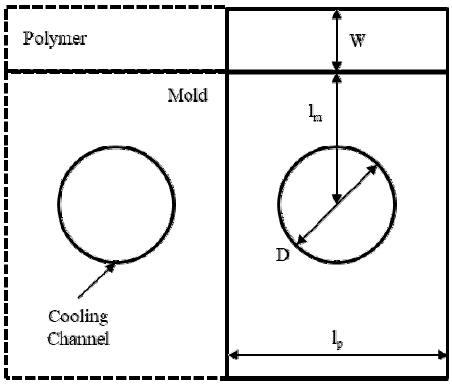
여기서 $$ {\overline{T}}_m$$는 금형 표면온도, T_c는 냉각수의 온도, ρ_p는 수지의 밀도, C_p는 수지의 비열, l_p는 냉각관의 간격, K_m는 금형의 열전도계수, W는 제품의 두께, h는 냉각수의 대류 열전달계수, D는 냉각관의 직경, l_m는 냉각관의 깊이, T_melt는 수지의 용융온도, T_eject는 수지의 취출온도, t_c는 제품의 냉각시간을 나타낸다.

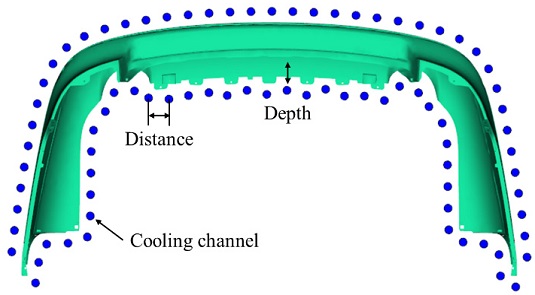
전술한 식을 도출하기 위해 사용된 변수들은 Fig. 1에 각각 표시하였다. 냉각관의 깊이 l_m는 금형 표면에서부터 냉각관의 중심까지의 거리를 의미하며 냉각관의 간격 l_p는 냉각관이 여러 개 설치될 때 두 냉각관 사이 중앙에서 다음 냉각관 사이 중앙까지의 거리를 의미한다.

Fig. 1

2D heat transfer model of the injection mold with cooling channel

수식 (1)에서 상수를 제외하고 변수들을 선정한다면 금형 표면온도 $$ {\overline{T}}_m$$, 냉각관의 직경 D, 냉각관의 깊이 l_m, 냉각관의 간격 l_p, 제품의 두께 W로 확인될 수 있다. 그러나 제품의 두께는 설계단계에서 결정되므로 마지막 남은 변수는 금형 표면온도, 냉각관의 직경, 깊이, 간격의 총 4개로 요약된다.

하지만 금형 표면온도는 Menges^[11]에 의하면 사전에 알려진 값들로 추정할 수 있다. 그는 각 소재 별 권장되는 용융온도, 취출온도, 금형 표면온도를 정리하여 표로 제공하고 있으며 본 연구에서 사용하려는 PP, ABS, PC, PMMA에 대해서도 제공하고 있어 Table 1에 관련 정보를 표시하였다.

Table 1

Temperature conditions for PP and ABS

따라서 식 (1)에서 최종적으로 남겨진 변수는 냉각관의 깊이와 간격, 그리고 직경의 3개만 남게 되며 나머지 상수들을 좌변으로 이항하여 정리하면 식 (2)와 같이 나타낼 수 있다.

$\[ \frac{h\pi D{K}_m{t}_c\left({\overline{T}}_m-T_c\right)}{{\rho }_p{C}_p\left(T_{\text{melt}}{\text{-T}}_{\text{eject}}\right)}=\left(\frac{W}{D}+\frac{h\pi }{2K_m}{l}_m\right)\times l_p \]$

(2)

수식 (2)에서 변수는 우변으로 이항해서 나타냈으며 본 수식을 참고한다면 동일한 금형 표면온도를 가질 때 냉각관 깊이와 간격, 그리고 직경 사이의 정량적 관계성을 확인할 수 있다.

2.2 설계 그래프의 작성

식 (2)를 이용한 설계 그래프를 작성하기 위해선 소재의 물성 값이 필요하므로 대표적으로 많이 사용되는 LG화학의 PP 중 TE-5005, ABS 중 HF 380 그레이드와, PC 중 GN1008RF 그레이드, 마지막으로 LX MMA의 PMMA 중 IH830HF 그레이드를 선정한 후 Moldflow, 각 소재사가 제공하는 TDS(technical data sheet), 그리고 Menges^[11] 자료를 참고하여 계산에 필요한 정보들을 Table 2에 나타내었다.

Table 2의 값들을 이용하여 식 (2)에 대입 후 정리하면 PP용 식 (3), ABS용 식 (4), PC용 식 (5), PMMA용 식 (6)을 얻을 수 있다. 그런데 수식을 참고하면 괄호안의 W/D 항이 2791.11×l_m 항보다 값이 매우 작음을 확인할 수 있다.

$\[ 8.682=\left(\frac{W}{D}+2791.11\times l_m\right)\times l_p \]$

(3)

$\[ 5.931=\left(\frac{W}{D}+2791.11\times l_m\right)\times l_p \]$

(4)

$\[ 2.930=\left(\frac{W}{D}+2791.11\times l_m\right)\times l_p \]$

(5)

$\[ 5.582=\left(\frac{W}{D}+2791.11\times l_m\right)\times l_p \]$

(6)

Table 2

Material data for PP TE-5005, ABS HF 380, PC GN1008RF and PMMA IH830HF

일반적인 사출성형에서 제품의 두께는 2~4 mm 내외이며 냉각관의 직경은 5~20 mm 이내이므로 W/D 항의 최대값을 사용해도 0.8 수준이다^[11]. 하지만 냉각관의 간격은 건드릴 가공의 제약으로 인해 직경의 최소 2배 이상을 사용해야 하므로 5 mm 냉각관을 사용해도 간격은 최소 10 mm는 유지해야 한다. 따라서 이 때의 간격 값을 2791.11×l_m 항에 넣고 계산하면 27.91로 W/D 항의 최대값 보다도 약 30배 정도 큰 값을 가지므로 W/D 항은 계산 결과에 영향도가 매우 낮음을 확인할 수 있다.

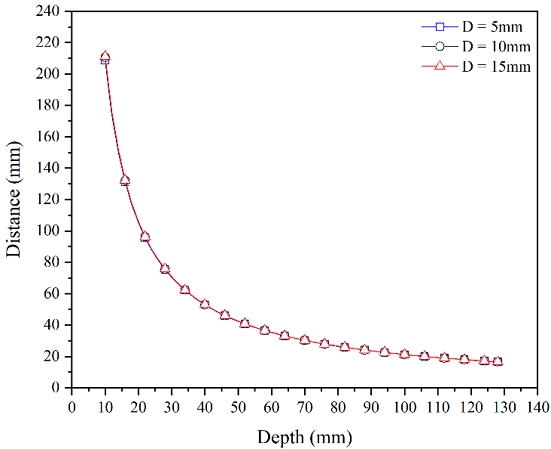
Fig. 2에는 ABS용 식 (4)에 W/D 항을 넣고 제품의 두께는 2.5 mm 인 경우를 가정하여 냉각관 직경을 5, 10, 15 mm로 변경하면서 냉각회로 설계 그래프를 그린 결과를 나타냈다.

Fig. 2

Cooling channel design graph for ABS using equation (3)

Fig. 2를 확인결과 냉각관의 직경이 변해도 깊이와 간격에는 영향도가 낮음을 확인할 수 있었기에 식 (3)과 식 (4)의 W/D 항을 삭제하고 단위를 mm로 변환시킨 후 최종적으로 정리한 수식은 다음과 같이 나타낼 수 있었다.

$\[ 3110.4=l_m\times l_p \]$

PP (7)

$\[ 2124.9=l_m\times l_p \]$

ABS (8)

$\[ 1049.7=l_m\times l_p \]$

PC (9)

$\[ 2000.0=l_m\times l_p \]$

PMMA (10)

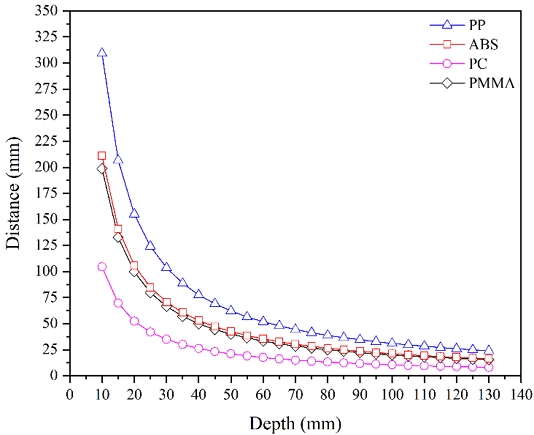
식 (7), 식 (8), 식 (9), 식 (10)를 이용해 최종적으로 작성된 냉각회로 설계 그래프는 Fig. 3에 나타내었다. PP와 ABS소재를 사용하는 각각의 경우를 하나의 그래프에 나타냈으며 PP가 상대적으로 넓은 설계 범위를 가짐을 확인할 수 있었고 반대로 PC의 설계 범위가 가장 좁음을 확인할 수 있었다.

Fig. 3

Cooling channel design graph for PP, ABS, PC and PMMA

2.3 설계 그래프의 적용

전술한 내용을 실제 제품에 적용해 보았다. 제품은 자동차 범퍼이며 LG화학의 PP TE-5005 소재를 이용하여 성형 되는 제품이다. Fig. 4에 해석에 사용된 형상을 나타냈으며 제품의 평균 두께는 2.8 mm로 확인되었다. 범퍼의 대략적 크기는 가로×세로×높이가 약 1800×500×350 mm이었고, 해석에 사용된 프로그램은 Autodesk사의 Moldflow Synergy 2021 이다.

Fig. 4

Automotive front bumper

생성된 요소의 종류는 삼각형, 요소의 개수는 약 3만개이며 냉각해석만 수행하였고 냉각시간은 Yu^[12]의 자료를 참고해 11.5초로 입력 후 설계 그래프의 적용 결과를 검증하였다. 사용된 소재가 PP 이므로 Table 2의 값들을 참고하고 식 (2)를 사용해 PP 냉각회로 설계용 그래프를 작성 후 Fig. 5에 나타내었다.

Fig. 5

Cooling channel design graph with the restricted area

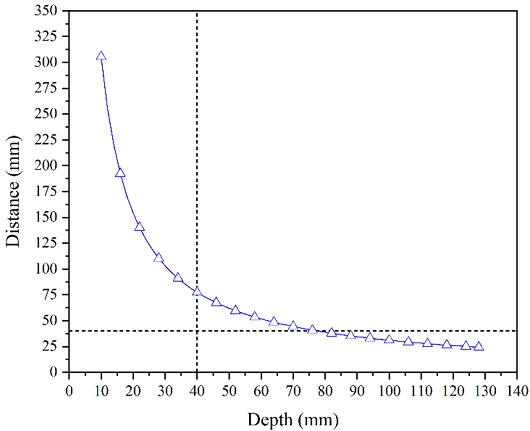
그러나 설계를 진행할 때 가공상의 한계로 인해 냉각관의 깊이와 간격의 제약사항이 발생한다. Menges^[10]에 의하면 냉각관의 깊이와 간격은 최소한 직경의 2배 이상은 확보해야 냉각관 건드릴 가공 시 가공 불량이 최소화 된다고 알려져 있다. 따라서 냉각관의 직경을 일반적인 범퍼 금형에 사용하는 Ø 20로 사용한다면 냉각관의 최소 깊이와 간격은 40 mm 이상으로 설계해야 하며 Fig. 5에 전술한 설계 불가 영역을 실선으로 표시한 PP용 설계 그래프를 나타냈다.

Fig. 5를 참조하면 가공 상의 한계로 인해 설계 가능한 깊이와 간격의 범위가 좁아 졌으며 냉각관의 깊이는 약 40 mm~80 mm 사이 냉각관의 간격은 약 40 mm~80 mm 수준으로만 변경이 가능함을 확인하였다. 전술한 내용을 기준으로 냉각관의 깊이가 각각 40 mm와 70 mm의 두 경우만 선정하여 냉각관을 생성한 후 냉각 해석을 수행하여 결과를 확인하였다. 냉각관이 생성된 그림은 Fig. 6, Fig. 7에 냉각 해석 후 제품 온도는 Fig. 8에 각각 나타내었다.

Fig. 6

Cooling channel design when the depth is 40 mm

Fig. 7

Cooling channel design when the depth is 70 mm

Fig. 8

Local hot spot area of the product

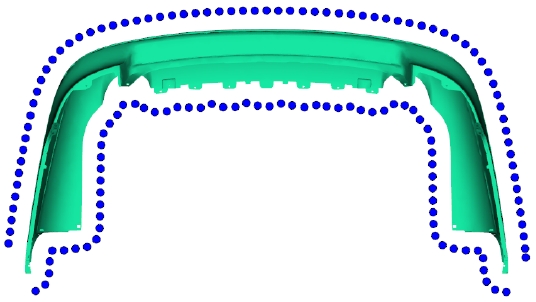
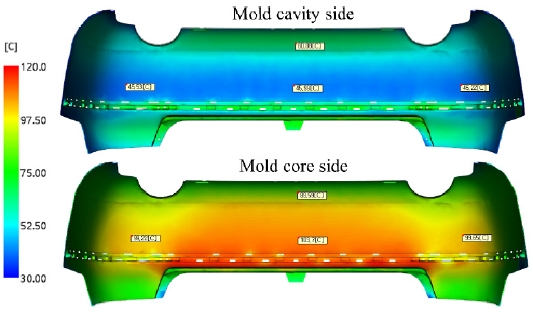
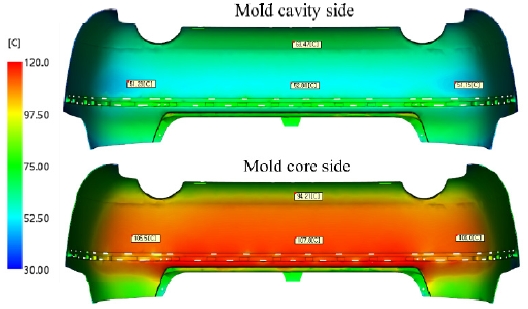
Fig 6은 냉각관 깊이를 40 mm로 정하고 수식 (6)을 이용해 냉각관 간격을 약 77.8 mm로 계산한 후 냉각관을 생성한 결과이며 Fig. 7은 냉각관 깊이를 70 mm로 정하고 수식 (5)을 이용해 냉각관 간격을 약 44.4 mm로 계산한 후 냉각관을 생성한 결과를 나타냈다.

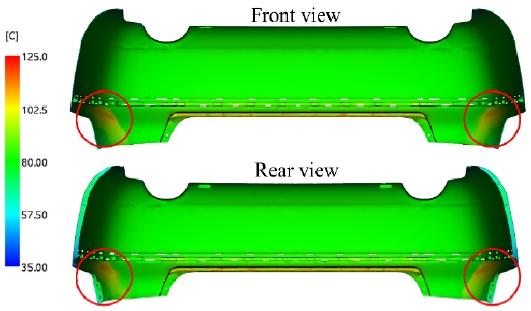
Fig. 8은 Fig. 6의 냉각 해석 후 제품의 온도분포를 나타낸 결과이며 전반적으로 냉각이 균일하게 잘 수행되었으나 원으로 표시한 두께 방향으로 급격한 깊이 변화가 발생하는 영역에선 냉각이 부족함을 확인할 수 있었다. 이는 제품의 표면 형상을 완벽히 따라가지 못하는 직선형 냉각관의 한계점이다.

다음으로 금형의 캐비티와 코어측 온도를 Fig. 9에 나타내었다. 확인결과 금형 캐비티측은 냉각이 잘 수행되었음을 확인할 수 있었으나 볼록한 제품 형상으로 인해 직선형 냉각관과의 거리가 먼 코어측에서는 상대적으로 온도가 높음을 확인할 수 있었으며 배플관, 버블러 등의 부가적인 냉각요소를 사용한다면 본 현상은 개선할 수 있다.

Fig. 9

Mold cavity and core surface temperature when the depth is 40 mm

Fig. 10

Mold cavity and core surface temperature when the depth is 70 mm

다음으로 냉각 해석을 수행한 후 설치된 냉각 회로의 성능을 확인하기 위해 제품의 평균온도 및 온도편차를 확인하였다. 먼저, 평균온도를 확인했을 때 Fig. 6의 경우엔 약 87.3℃, Fig. 7의 경우엔 약 82.9℃로 확인되었다.

초기 깊이와 간격의 관계식을 유도할 때 일정한 금형 표면온도를 유지하는 조건으로 정리된 수식이기에 약 4.4℃의 차이는 일반적인 사출성형 공정 조건을 고려할 때 무시 가능한 범위로 수식을 잘 따라 감을 확인할 수 있었다.

온도편차의 경우에도 Fig. 6의 경우 12.0로 Fig. 7의 경우엔 11.8로 계산되었다. Fig. 7의 경우엔 냉각관이 많이 설치되어도 제품에서의 거리가 먼 상태에서 냉각관의 간격이 좁기에 Fig. 6의 냉각 해석 결과와 큰 차이가 나지 않는다.

마지막으로 본 연구에서는 냉각관 직경의 영향도를 낮게 확인해 무시하고 냉각관 설계 그래프를 작성했기 때문에 해석에서 냉각관 직경을 변화시켜 영향도를 실제로 확인하였다. 두 해석모델에 대해 냉각관 직경만 Ø10, Ø30로 변화시켜 추가해석을 수행했으며 해석수행 결과 평균온도와 온도편차값을 Table 3에 요약해 나타내었다.

Table 3

Cooling analysis results according to the diameter change

Table 3의 냉각해석 결과를 확인해도 실제 냉각관의 직경 변화는 냉각해석 결과 중 평균온도와 온도편차값에 영향도가 매우 낮음을 확인할 수 있다. 해석에서는 냉각수의 유량이 일정하다고 가정하고 냉각해석을 수행하므로 냉각관 직경이 커지면 그에 비례해 냉각수의 속도가 감소된다. 따라서 직경의 증가로 열전달 면적이 커져서 발생하는 열전달량 증가 효과와 냉각수의 속도 저하로 인한 열전달량 감소 효과가 상쇄되어 냉각관 직경의 영향도가 낮아진다고 판단했다.

3. 결 론

본 연구에서는 냉각회로 설계 그래프를 이용 사출금형용 직선형 냉각회로를 정량적으로 설계할 수 있는 방법론을 개발하였다. 특히나 별도의 해석프로그램 없이 빠르게 설계할 수 있도록 구성하여 일정이 촉박한 양산공정에서도 충분히 활용할 수 있도록 만들었다.

냉각회로 설계 그래프의 제작을 위해 참고한 내용은 Xu의 연구결과였다. Xu는 일정시간 냉각 후 금형표면온도를 추정하기위한 수식(1)을 제안하였는데 본 연구에서는 수식(1)과 사용되는 소재의 물성값을 대입한 후 정리하여 냉각관의 깊이와 간격, 직경간의 관계식을 유도했다. 이 때 사용되는 소재는 일반적인 사출성형에 많이 사용되는 PP와 ABS, PC, PMMA를 기준으로 관계식을 유도하여 냉각회로 설계 그래프를 제작하였다.

냉각회로 설계 그래프 확인 결과 냉각관의 직경은 영향도가 낮은 인자로 확인되어 냉각관의 깊이와 간격만으로 단순하게 구성된 설계 그래프를 만들었고 이를 이용하여 실제 자동차의 범퍼 제품에 적용하여 그 효과를 검증하였다. 자동차의 범퍼는 PP를 사용하여 제작되기에 PP의 냉각회로 설계 그래프를 이용하여 총 두 경우의 냉각회로를 설계한 후 냉각해석을 수행하였다.

냉각관의 깊이 40 mm, 간격 77.8 mm인 경우와 냉각관의 깊이 70 mm, 간격 44.4 mm인 두 경우에 대한 냉각해석 결과 평균온도는 4.4℃차이 온도편차는 0.2 차이로 실제 사출성형 공정 조건을 고려한다면 무시 가능한 차이로 두 냉각회로는 유사한 냉각효율을 가진다고 볼 수 있다.

또한 냉각관의 직경을 변화시켜 고안된 수식의 검증을 수행한 결과 직경의 영향도가 실제로 낮음을 확인해 냉각회로 설계 그래프의 신뢰성을 높일 수 있었다. 개발된 방법론을 이용한다면 금형 설계자는 금형 구조 및 취출핀 등의 필수요소를 고려해 간섭이 발생하지 않는 간격과 깊이를 선정하고 금형설계에 활용한다면 해석 및 최적화로 인한 시간 소모 없이 신속한 냉각회로의 설계가 가능해진다.

추후 연구에선 해석 과정 중 확인된 제품의 두께 방향으로 깊이 변화가 커서 직선형 냉각회로 설치가 어려워 온도가 상대적으로 높은 영역에서 주로 사용되는 배플관의 설계까지 포함시킨 수식을 정리해 냉각회로 설계 그래프의 적용 범위를 더욱 넓힐 계획이다.

Acknowledgments

이 연구는 2022년도 광주대학교 대학 연구비의 지원을 받아 수행되었음.

References

• Kwon, T. H., Park, S. J., 1998, Optimal Cooling System Design for the Injection Molding Process, Polym. Eng. Sci., 38:9 1450-1462. [https://doi.org/10.1002/pen.10316]
• Rhee, B. O., Park, C. S., Chang, H. K., Jung, H. W., Lee, Y. J., 2010, Automatic Generation of Optimum Cooling Circuit for Large Injection Molded Parts, Int. J. Precis. Eng. Manuf., 11:3 439-444. [https://doi.org/10.1007/s12541-010-0050-z]
• Choi, J. H., Choi, S. H., Park, D. H., Park, C. H., Choi, D. H., Rhee, B. O., 2012, Design Optimization of Injection Mold for Minimizing Temperature Deviation, Int. J. Automot. Technol., 13:2 273-277. [https://doi.org/10.1007/s12239-012-0024-5]
• Sachs, E., Wylonis, E., Allen, S., Cima, M., Guo, H., 2000, Production of Injection Molding Tooling with Conformal Cooling Channels Using the Three Dimensional Process, Polym. Eng. Sci., 40:5 1232-1247. [https://doi.org/10.1002/pen.11251]
• Dang, X. P., Park, H. S., 2011, Design of U-shape Milled Groove for Conformal Cooling Channels for Plastic Injection Mold, Int. J. Precis. Eng. Manuf., 12:1 73-84. [https://doi.org/10.1007/s12541-011-0009-8]
• Kanbur, B. B., Suping, S., Duan, F., 2020, Design and Optimization of Conformal Cooling Channels for Injection Molding: A Review, Int. J. Adv. Manuf. Technol., 106:7 3253-3271. [https://doi.org/10.1007/s00170-019-04697-9]
• Feng, S., Kamat, A. M., Pei, Y., 2021, Design and Fabrication of Conformal Cooling Channels in Molds: Review and Progress Updates, Int. J. Heat Mass Transf., 171 121082. [https://doi.org/10.1016/j.ijheatmasstransfer.2021.121082]
• Gao, Z., Dong, G., Tang, Y., Zhao, Y. F., 2021, Machine Learning Aided Design of Conformal Cooling Channels for Injection Molding, J. Intell. Manuf., 1-19. [https://doi.org/10.1007/s10845-021-01841-9]
• Ko, Y. H., Kim, D. E., Kim, D. H., Kim, Y. D., Kim, J. S., Kim, J. S., Kim, T. B., Song, J. H., Lee, J. S., Lee, J. S., Ha, C. W., Cheon, H. P., 2021, 2021 PPURI Industry White Paper, Korea National Ppuri Industry Center, Korea.
• Xu, X., Sachs, E., Allen, S., 2001, The Design of Conformal Cooling Channels in Injection Molding Tooling, Polym. Eng. Sci., 41:7 1265-1279. [https://doi.org/10.1002/pen.10827]
• Menges, G., Micaheli, W., Mohren, P., 2001, How to Make Injection Molds, Third Edition, Hanser Publications, Germany. [https://doi.org/10.3139/9783446401808.fm]
• Yu, C. J., Sunderland, J. E., 1992, Determination of Ejection Temperature and Cooling Time in Injection Molding, Polym. Eng. Sci., 32:3 191-197. [https://doi.org/10.1002/pen.760320305]