안정적인 비접촉 파지를 위한 스월 형성 컵의 팁 구조 개선

1. 서 론

현대 정밀 산업에서는 제조 및 공정 방식에 따라 다양한 이송을 위한 파지법이 적용되고 있으며 그 방법은 고도의 생산 환경에 의해 점점 전문화되거나 특이한 기능들을 가지는 추세를 보여주고 있다^[1]. 특히 자동화 공정에서는 로봇 기능을 이용하는 장치 구성으로 공정 간에 다각도에서 부품을 집어 올리거나 배치(picking & placing)하는 접근 수단들이 제공되고 있다. 여러 수단 중에서 로봇 핸드의 엔드 이펙터(end efftor)가 공압을 이용하여 물체를 들어 올리는 파지 능력은 대부분 진공에 의한 흡착 힘으로 이루어진다^[2]. 강한 힘은 진공펌프로 이루어지며 약한 힘은 벤튜리(venturi) 원리 등을 적용한 진공 발생기의 흡입 모듈에서 저압과 대기압의 차이로 직접 흡착시키는 기능을 갖는 것이 대표적인 형태이다^[3,4]. 엔드 이펙터에 적용되는 이러한 모듈들은 단순히 진공을 일정 영역 내에서 구속하여 얻는 힘으로 물체를 접촉하여 파지하는 핸들링 기술이며 이미 많은 분야에서 확대 적용되고 있다^[5]. 특히 최근 몇 년 동안 지속된 비대면 생활의 일상화 패턴을 거치면서 제조 작업 환경뿐만 아니라 날로 증가하는 물류 작업의 증가는 이송 처리작업의 속도와 자동화에 대한 필요성을 더욱더 요구하는 실정이다.

앞서 언급한 직접 접촉 방식은 모듈과 공정 부품의 표면 사이를 완벽하게 밀봉하는 진공 환경을 가지는 가장 간단하면서 핸들링할 수 있는 다양한 형태로 사용 범위를 가지고 있으나, 일부 적용 곤란한 흡착면의 형상과 흡착면에 대한 직접적인 접촉이라는 한계점이 있다. 오늘날 반도체, 디스플레이 등의 초미세 공정에서 이루어지는 일부 제작품들은 스크래치나 오염원 등이 매우 심각한 품질 저하의 원인이 되기 때문에 표면을 보호해야 하고 초정밀 소자가 존재하는 면은 직접적인 접촉은 피해야 한다^[6]. 따라서 이러한 문제점을 극복하기 위하여 웨이퍼나 패널들의 제작 공정에서는 파지와 배치를 다루는 베르누이(Bernoulli)의 원리를 적용하는 비접촉 소형 모듈을 일부 사용하고 있다^[7-9].

이 방식은 주입 공기를 컵 밖으로 토출시키면서 컵 가장 주변부에서 비접촉 접점을 유지함과 동시에 컵 내부 중앙부에서는 일정 이상의 진공 영역을 동시에 확보하여 제작품이 비접촉 파지 되는 경우이다. 이때 벤투리나 진공펌프에서 생성하는 진공을 이용하여 별도 연결되는 접촉 패드(suction pad)가 물체 표면에 완전히 흡착되어 힘을 갖는 것과는 다르게 비접촉 간격을 유지하기 위해서는 두 가지 다른 힘(작용 방향 기준)이 동시에 일정 거리를 두고 평형 상태에 존재하게 된다.

따라서 비접촉 파지 기능을 갖기 위한 컵 모양의 대표적인 모듈은 컵 내부 자체 구조가 유체의 운동에너지로부터 성향이 다른 두 힘을 얻어내는 형태여야 한다. 또한 비접촉 미세 틈새(0.3 mm~1.0 mm) 수준을 확보하기 위하여 외부로 끊임없이 일정하게 공기를 토출해야 하는 동안 불안정한 유동(fluid motion)에 대한 제어가 필요하다. 지금까지 이 부분에 주안점을 두고 많은 연구가 이루어져 왔으며, 대체로 소형 공작물을 대상으로 하는 비접촉 파지 능력(1~5 N)에 해당하는 보텍스나 베르누이 흐름을 이용하는 원리에 근거를 둔 연구가 실험 또는 수치해석으로 주로 고찰되었다^[10-12].

베르누이 원리를 이용하는 경우 컵 깊이(내부 높이)가 작은 공간에서도 내부 중심에서 방사 방향으로 직접 흐름을 진행하거나 중앙 하단부로 향하는 흐름을 원주 쪽으로 이동하는 채널을 두어 진공을 확보하는 구조로 개선^[9]을 거듭하고 있으며, 보텍스 방식은 토출하는 지점 하단부의 팁 형상과 내부 공간을 제어하는 연구^[13]가 집중되어 있다. 대다수 연구들은 실험이나 수치해석에서 일정 틈새가 발생/유지되는 환경에서 측정 또는 계산되는 압력/힘을 분석하고 있으며 여기에 관련되는 공기의 소모량, 비접촉 거리별로 형성되는 부상력을 토대로 컵의 다양한 구조에 대한 최적화에 설계 결과물이 도출되고 있다^[10,14,15].

흐름의 형태상 베르누이에 비해 보텍스 방식은 스월 흐름을 위해 공간이 더 필요한 대신 진공을 높게 얻을 수 있다. 그러나 스월 흐름 특성인 토크가 발생하고 그로 인해 불안정한 파지가 나타날 수 있다. 대신 컵 직경을 확대하여 파지 능력을 증가시키는 것이 가능하다. 이에 따라 무거운 평판 작업물을 대상으로 필요한 비접촉 파지력을 얻기 위해 요구되는 공기의 운동에너지를 공기 소모율을 늘리거나 컵 내부에서 기류 통로를 제어하거나 다른 진공 발생 원리를 복합 활용하는 등의 다양한 새로운 방안들이 발표되고 있다^[13,16,17].

현재 상용화 되어 있는 보텍스 컵의 비접촉 파지 능력은 몸체 외경(최대 100 mm)에 공기 소모율(최대 258 L/min)을 적용하여 44 N 파지까지 가능하다^[5]. 강성의 큰 평판을 비접촉으로 파지하기 위해서는 보텍스 컵을 포함하여 큰 제원의 사용이 불가피하고 다수의 컵을 사용해야 한다^[17]. 그리고 생성하는 기류의 안정적인 거동과 힘의 균형에 의한 비접촉 위치(sweet spot) 확보를 위하여 보텍스 컵의 제원에 따른 내부 거동에 대한 종합적인 평가와 함께 부상력에 미치는 관련성을 검토할 필요가 있다.

따라서 본 연구는 보텍스 방식의 비접촉 컵 형상 설계에 대하여 개선 방안을 고찰하고자 한다. 세부적으로 컵의 제원별(공기 소모량, 직경, 높이 등)로 내부에서 거동하는 흐름을 스월수로 표현하여 비교 분석하며, 하단 팁의 형상 변형과 컵 내부의 흐름 가이드 블록으로 끝단의 유동 흐름에 변화를 주어 최대한 진공 발생을 돕고 컵 하단부에서 유지되는 에너지 사용 효율을 최대한 높여 안정된 파지 유효거리와 파지 성능을 동시에 확보하고자 한다.

2. 팁(끝 단) 홈과 흐름 가이드 블록을 갖는 에어 컵

2.1 보텍스 에어 컵의 기본 구조

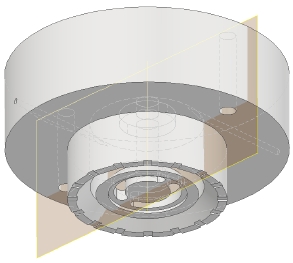
공압을 이용하는 보텍스 흐름 구조의 가장 간단한 원리 및 구조는 원통 벽에 접선 방향으로 존재하는 강력한 스월(swirl)이 주유동 흐름의 경계를 통하여 전단 및 순환 패턴을 형성하면서 내부에 진공을 생성한다. Fig. 1과 같이 컵의 내부 벽을 따라 주입되는 기체의 유입율($$ {\dot{Q}}_i$$)과 내부의 진공 발생 공간을 위해 필요한 내경(D_i) 및 높이(H)가 어느 정도 필요하고 토출되는 영역에서 흐름에 관여되는 팁(tip, T)의 존재가 기본 구조이다. 그리고 이들 관계는 상호 연관성도 매우 높다.

Fig. 1

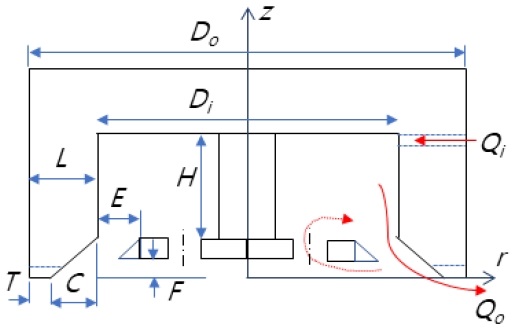
The schematic diagram for a non-contact vortex cup with a separated airflow guide and serrated tip groove

컵 하단 팁 주변은 각속도와 축 방향 속도 성분이 상충하는 곳이어서 토출에 용이한 45^o의 모따기(C) 형태를 기본으로 유지한다. 이와 관련된 선행 연구에서는 보텍스 컵 팁의 크기인 T와 C의 크기를 일정하게 두고 내경 40 mm에 기준 높이 30 mm를 변화시켜 나타나는 내부 진공 발생의 효율적인 결과를 도출한 바 있다^[15,17]. 이를 근거로 팁 길이와 모따기 크기와 관련한 형상은 컵 성능(파지)에 변화를 줄 수 있는 요소이다.

3. 해석 모델링

3.1 해석 모델링 및 계산 설정

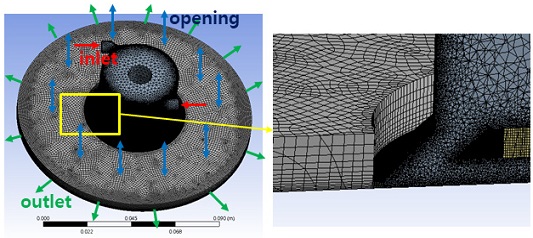
Fig. 2는 에어 컵 기본 구조에 3구 관통홀 가이드 블록과 16개 팁 홈이 존재하는 모델이다. 해석 모델은 고체 부분 영역을 제외하고 컵 하단 토출 외부 영역을 포함하는 유체영역(fluid domain)을 포함하면 Fig. 3처럼 되며, 컵 하단에 일정 비접촉 거리를 두고 평판(벽)이 배치된다.

Fig. 2

The newly suggested non-contact vortex cup with a guide block and tip grooves

Fig. 3

The mesh for the computational domain of an air cup

컵의 파지 능력은 비접촉 거리의 변화에 따른 성능 비교 계산으로 이루어지며, (i) 컵 본체, (ii) 컵 본체 + 가이드 블록, (iii) 컵 본체 + 팁 홈 등으로 적용되는 모델링으로 구성된다. 보텍스 컵의 내부 스월 흐름에 대한 평가는 축 방향 위치별로 축 운동량의 유량에 대한 각운동량의 유량의 비율로 정의^[18,19]되는 식(1)의 스월수(swirl number, S)로 표현하여 컵 구조에 따른 유동의 특성을 비교한다.

$\[ S=\frac{{\int }_0^{D_i/2}\rho u_z\left(r{u}_{\theta }\right)rdr}{R{\int }_0^{D_i/2}\rho u_z^{2}rdr} \]$

(1)

여기서 R은 컵 높이별 최대 반경, u_z는 축 방향의 속력이며, u_θ는 원주 방향의 속력이다. 식(1)에서 스월수는 임의 영역의 전체(global)를 표현하나 가이드 블록 등의 존재로 지역적(local)으로 계산될 수도 있다. 스월수에 관여되는 D_i, H의 값과 기타 제원은 Table 1에 나타냈으며, 상용품^[4,5] 제원에 근접하고 이전 연구^[15-17]에서 다루었던 컵의 제원과 동일하거나 유사하다.

Table 1

Geometry dimensions

3.2 해석 방법

해석 도구는 CFX이고, 적용하는 지배방정식은 연속, 운동, 난류(k-ε) 방정식들이며 여기에 비압축성과 정상 상태 해석을 적용했다. 실제 컵은 공기를 공급받고 빠른 반응시간 내에서 파지 힘을 생성하여 평형 상태를 유지한다. 이전 계산 및 실험적으로 확인된 유효 비접촉 거리(h)는 0.3 mm에서 0.9 mm로 변화시켰고, 컵 팁에서 하단에 파지 물체가 위치하는 것으로 가정하여 정상상태 해석을 수행하였다.

Fig. 3의 해석 도메인의 격자망은 기본 Tetra 모양을 가지며 일부 영역은 Hexagonal 모양으로 처리되며, 컵의 내부 벽 주위와 샘플 표면 위 그리고 토출 부위는 급격한 물리량의 변화가 존재하기 때문에 조밀한 비균등 Tetra 격자가 적용되었다. 격자수는 450만 개 수준까지 이루어졌으며 격자 밀도에 따른 신뢰값 판단은 컵의 파지력 계산값을 대상으로 평가하여 조정하였다. 수치계산 수렴 조건은 10^-4를 적용했다. Table 2는 경계조건 설정 조건을 나타내며 이에 대한 위치는 Fig. 3에 도시했다. 경계조건 중 2개 주입 포트에 적용한 주입 압력은 각각 1~3 bar까지 사용했으며 여기에 해당하는 유입 총질량 유량은 2.72×10^-3 kg/s ~ 4.71×10^-3 kg/s를 가진다.

Table 2

Settings the analysis mode

4. 계산 결과 및 고찰

4.1 보텍스 컵의 기본 성능 해석

4.1.1 기본 구조 보텍스 컵의 유동 패턴

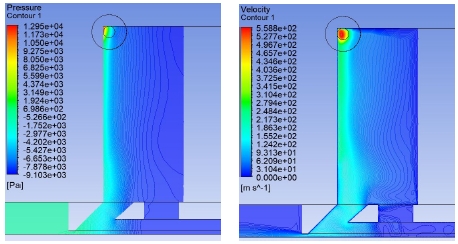
Fig. 4는 대용량 컵 기본 본체(D_i:H = 4:3, T = 1 mm, h = 0.6 mm)에 질량 유량 3.84×10^-3 kg/s (2 bar 작동 압력에 대응)을 사용했을 때 안정적인 스월 흐름으로 내부 진공을 생성하는 모습을 보여준다. 팁 하단부에서 0.6 mm의 비접촉 토출 간격을 유지하는 조건에서 속도, 압력 분포. 속도장 그리고 유선이 형성된다. 이러한 패턴 형태는 유입과 유출의 상태에 맞게 설정된 조건에 따라 물리적 요인들이 균형을 맞추기 위해 컵 내부에서 작용하면서 나타난 결과이다.

Fig. 4

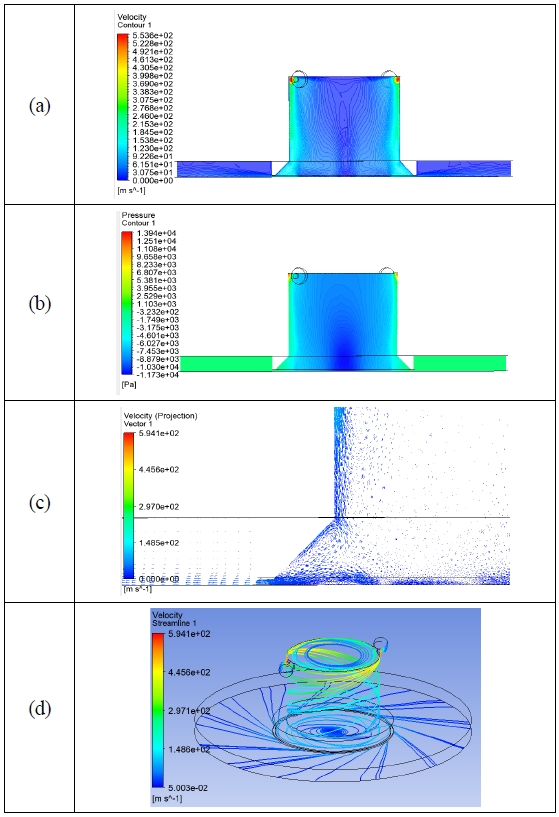
Typical motion of the basic vortex cup; 1 mm tip length, 0.6 mm air gap, 3.84×10-3 kg/s mass flow rate; (a) velocity, (b) pressure, (c) vector-enlarged and (d) streamline

Fig. 4(a)에서 월 젯(wall jet)에 의해 컵 벽의 곡률에 따라 벽 쪽에 유지되는 강한 스월 흐름을 가지기 때문에 속도구배는 벽 가까이에서 가파르게 이루어졌다. 또한 이러한 흐름에 의한 속도구배와 유사하게 Fig. 4(b)의 압력 구배를 형성하고 있다.

벽 쪽의 높은 운동에너지를 갖는 주 흐름의 경계를 통하여 전단 작용이나 그 주변의 크고 작은 순환과 같은 흐름으로 지속적인 진공 펌핑과 같은 역할이 이루어져 스월 운동이 약한 중심 영역에서부터 진공이 형성된다. 따라서 보텍스 컵에서 안정적인 진공을 얻기 위한 조건은 압력 구배(물리량의 변화)가 벽 쪽에서 형성될 수 있는 내부 구조 환경이 요구된다. 이러한 구배에 의한 진공과 양압의 절대값이 동시에 크면 클수록 비접촉 거리 확보와 평판에 대한 진공 파지가 유리해진다. Fig. 4(c)에서 벡터장을 보면 모따기 영역인 스월 운동의 종착점에서 물체 표면을 통하여 토출 방향 진행과 함께 안쪽으로 유입하는 순환을 볼 수 있으며, 이때 팁의 형상이 비접촉 간격이나 진공 영역에 영향을 주게 된다. 그리고 Fig. 4(d)는 나선형으로 이루어지는 유속 흐름의 특징을 보여주고 있다. 여기서는 회전하는 나선각과 축 방향 운동량이 미치는 상호 영향력을 볼 수 있으며 최종 토출되는 나선 흐름을 알 수 있다.

4.1.2 스월수에 따른 유동 분석

각종 흡입 포트 등에서 사용되는 선회 유동은 목적에 따라 여러 형태를 가진다. 대표적인 흐름인 스월은 유동의 접선 방향 속도 성분이 커지면 축방향 속도는 줄면서 속도구배와 유동이 선회하는 영역에 변화를 주게 된다. 따라서 컵 내부의 스월 유동을 무차원 스월수(S)를 사용하여 컵 내부의 운동량 변화를 간접 비교했다.

이때 식(1)의 계산 표현식은 CFX Expression Lanauage (CEL)를 이용하여 계산되었다. 이때 사용되는 적분, 최대값 등을 위한 연산 함수는 areaInt(), maxVal(), sqrt() 등이 적용된다. 그리고 직교 좌표계 시스템(u, v, w velocity components in X, Y, Z coordinate)을 사용했으며 해당 계산 영역인 원통의 축 방향에서 수평으로 형성되는 임의의 평면은 @Plane 1 등으로 지정되었다.

Fig. 5(a)는 기본 본체 컵에 공기 주입량만을 달리했을 때 컵 내부 천정으로부터 하단 축방향으로 5, 10, 22 mm에 위치하는 3개 수평면에서 계산된 스월수와 파지력을 나타내었다. 0.6 mm 비접촉 갭 유지에서 유량 변화를 줄 때 스월수를 보면 상부에서는 5.3 이상을 유지하다가 5.0 이하로, 그리고 토출부 영역인 팁 모따기 영역 전 단계 위치에서는 3.5까지 떨어졌다. 초기 높은 스월수는 축 방향으로 토출 위치 쪽으로 진행함에 따라 저하되고 있으나 공기유량 변화에는 영향이 적다. 이것은 컵 하부로 진행될수록 각운동량이 줄어들고 토출부 가까이서 물체 표면 위로 내부 유입 또는 순환하는 흐름이 존재하기 때문이며, 공기유량에 의한 에너지 사용 증감은 전체적으로 파지력 변화에 큰 영향을 주지만 상대적인 운동량 비율에는 큰 변화가 없는 것으로 보인다.

Fig. 5

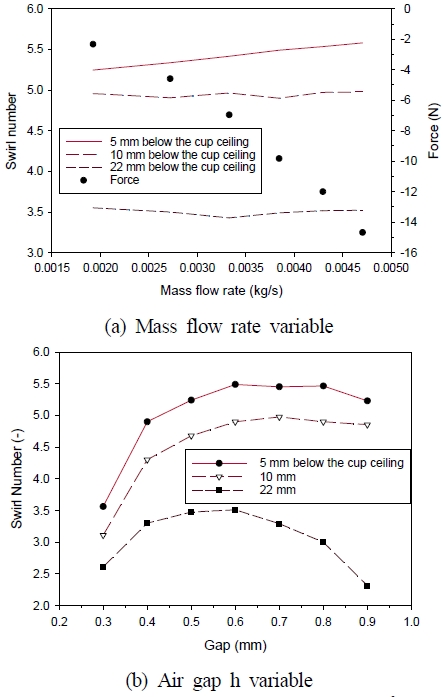
Swirl number vs gap (based on the 3.84×10-3 kg/s mass, 40 mm inner cup diameter, Di :H = 4:3, 0.6 mm air gap)

Fig. 5(b)는 유량(3.84×10^-3 kg/s)을 동일하게 적용하고 토출 갭의 크기(0.3~0.9 mm)를 다르게 했을 때 위치별로 계산한 스월수이다. 갭이 작은 경우는 토출에 필요한 추력(thrust) 증가와 함께 내부에 강한 순환이 이루어지는 이유로 적정 이상으로 갭이 큰 경우는 토출 시 저항 면적이 작아 축방향 속도가 커지는 이유로 각각 풀이된다. 즉, 컵 팁 영역 직전의 유동 흐름을 갭 크기별로 계산한 스월수만으로 유동 흐름을 판단해보면 비접촉 거리가 0.6 mm에서 스월수는 최대인 3.5를 유지 하는 수준을 보였다. 직경 40 mm인 기본형 보텍스 컵의 사용 예를 들어 가장 효율적인 스월 흐름을 가지는 부분을 스월수로써 최적인 비접촉 거리를 예측해볼 수 있었다.

4.1.3 컵 본체의 파지 성능 변화

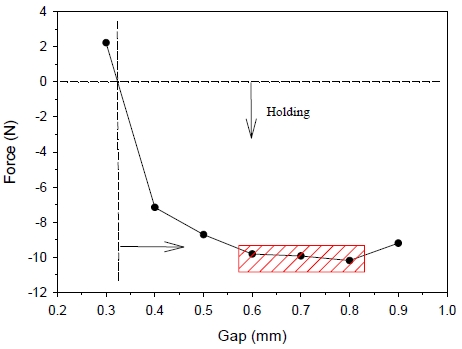
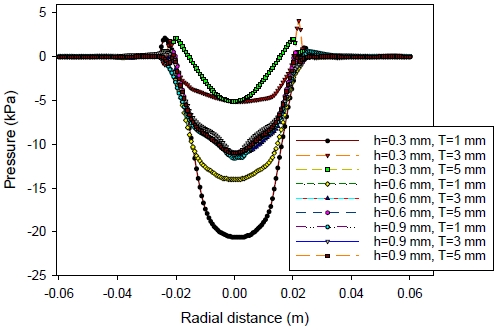
2 bar의 압력에 의한 질량 유량(3.84×10^-3 kg/s)을 사용하여 평판을 파지할 때 평형 유지하는 비접촉 거리를 0.3 mm에서 0.9 mm로 산정하여 계산된 파지력의 변화는 Fig. 6에 보여준다. 자중이 없는 경우에는 0.33 mm 갭부터 미는 힘을 상쇄하고 파지력이 형성되기 시작한다. 0.3 mm 갭 수준에서는 토출에 필요한 밀어내는 힘이 훨씬 크기 때문에 진공에 의한 파지력보다 우위에 있게 된다. 반대로 0.9 mm 갭 이상에서는 토출면의 확대로 각 운동량에 영향을 주게 되어 밀어내는 힘과 내부 진공 영역이 축소되기 시작했다. 따라서 Fig. 5(b)의 스월수 크기와 유사하게 최대 파지력 기준 갭 평형은 0.6 mm~0.8 mm에서 형성되었으며 실제 컵이 작동하면 여러 힘의 평형은 어떤 갭에서 미세하게 수렴 조정된다. 즉, 식(2)과 같은 조건에서 작업물이 자중(W)을 가지면 그만큼 힘의 균형을 위한 갭의 변화 진행되면서 힘의 평형 상태로 재조정된다.

$\[ {\left(F_{lifting}-F_{push}-W\ge 0\right)}_{gap} \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{g}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{ }\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{e} \]$

(2)

Fig. 6

Lifting force vs gap (h); 1 mm tip length, 3.84×10-3 kg/s mass flow rate

4.2 컵의 내부 구조 변경에 의한 성능 변화

4.2.1 컵 팁 길이 변화에 의한 효과

앞 소절에서는 비접촉 갭의 크기를 일정 범위에서 각각 고정한 후 인위적으로 컵 내부에서 형성되는 유동과 압력 분포에 따라 결정되는 컵 파지력을 계산했다. 이것은 컵 하단부 팁 길이를 최소화한 1 mm 수준에서 획득한 결과이다. Fig. 7은 비교를 위해 크게 갭의 간격을 0.3 mm, 0.6 mm, 0.9 mm으로 각각 고정하고 여기에 팁 길이를 1, 3, 5mm로 설계했을 때 파지력 변화 추이이다. 토출 영역 입구에서 시작되는 압력 강하 효과는 ∆p = K_L(1/2)ρV²으로 볼 수 있으며 여기서 손실계수 K_L = Φ(geometry)는 대부분 실용적 관점에서 형상만의 함수이다. 그리고 V는 토출 속도이다.

Fig. 7

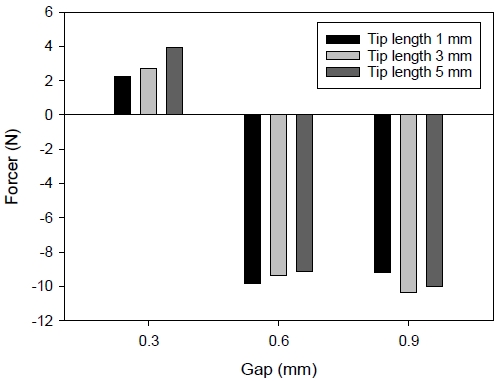
Lifting force vs gap; 0.3~0.9 mm air gap, 3.84×10-3 kg/s mass flow rate, different tip lengths, no grooved tip

팽창(expansion) 영역의 팁의 경사진 모서리 형상은 낮은 손실계수 유지가 가능하게 해주며 팁 길이를 연장하여 사용할 때 얻는 흥미로운 부분은 유효 비접촉 갭 범위를 벗어나는 0.9 mm인 경우, 1 mm 팁 길이 보다 3 mm 경우가 더 큰 진공 파지력을 가지는 것을 볼 수 있다. 이것은 팁의 길이 1 mm일 때 비접촉 갭의 크기가 0.6~0.8 mm에서 파지력에 있어 최적의 환경(Fig. 6 참조)인 반면, 팁의 길이를 3 mm로 늘이면 비접촉 갭의 크기가 0.9 mm에서 파지력이 떨어지는 것을 회복시켜주는 효과로 볼 수 있다. 그러나 팁 길이가 5 mm로 증가하는 경우 최적 성능을 위한 임계 수준을 벗어나는 것으로 나타났다. 따라서 사용 목적상 비접촉 갭의 크기를 증가시킬 필요가 있는 경우 팁의 길이를 늘여 이를 개선시킬 수가 있다.

4.2.2 컵 팁 홈에 의한 효과

보텍스 컵의 기본 본체는 비접촉 간격을 유지하는 힘의 균형 속에서 비접촉 판재와의 사이로 일정한 유량을 토출하게 되어 있다. 이 과정에서 유동이 Fig. 4(d)처럼 나선형으로 강하게 방출하기 때문에 단일 컵으로 파지 하는 평판 대상물은 불안정한 회전을 피할 수 없다. 그래서 2개 이상의 컵을 대칭형으로 구성하여 방지하고 있다. 따라서 팁 최종 하단부에 도달하기 전에 팁의 홈을 통한 일부 유출은 파지 물체에 대한 반력에도 영향을 줄 뿐만 아니라 이로 인한 중심으로 순환되는 유동의 거동에도 영향이 나타난다. 결국 팁 원주상에 홈 배열을 주는 구성의 일부 장점은 진공 형성 조건을 증대시키고 반력을 줄여 비접촉 거리를 조절할 수 있는 효과를 기대할 수 있다. 또한 일부 유량을 방사 방향으로 미리 유출하게 되어 앞서 제기한 파지 물체의 회전 문제를 완화할 수 있다.

Fig. 8은 보텍스컵 기본형에 하단 팁의 원주 방향으로 전체 갭의 토출 면적(π(D_i + C)h)에 비해 13%인 2.37×0.5 h 수준으로 16개의 홈(한 개의 홈 원주 길이 2.37 mm, 홈 높이 0.5 mm) 단면을 주고, 내부 쪽의 팁 길이를 1, 3, 5 mm로 각각 변화를 주었을 때 계산되는 파지력의 변화이다. 이때 동일한 질량 유량(3.84×10^-3 kg/s)을 사용하였으며, 팁 홈이 없는 경우인 Fig. 7과 비교해보면 파지력은 유효 갭의 범위 안에서 크게 상승하는 것을 알 수 있다.

Fig. 8

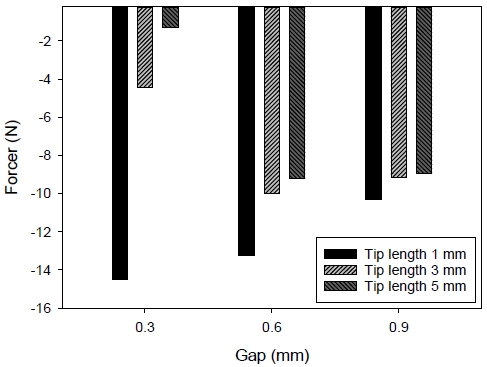
Lifting force vs gap; 0.3~0.9 mm air gap, 3.84×10-3 kg/s mass flow rate, different tip lengths, grooved tip

예를 들어 팁 길이 1 mm를 기준으로 홈이 없는 팁 구조에서는 0.6 mm 갭 수준에서 파지력이 좋게 나타났던 반면에 팁 홈이 존재하는 경우 0.3 mm 갭 수준에서 파지력이 우수하게 나타났다. 이 부분은 동일한 갭의 크기여도 홈을 통한 사전 토출량 만큼 내부 유동 패턴에 변화가 야기되었고 그만큼 힘의 균형을 위한 갭의 간격 조정이 필요했다. 그러나 팁 길이를 3 mm과 5 mm으로 유지하는 경우는 파지력에 대한 효율성의 변화는 크지 않았다. 따라서 팁의 형상과 관련하여 양압이 크게 상승하는 부분을 완화하는 목적으로 팁에 홈(groove)을 주는 부분이 있으며, 이 홈의 설계는 비접촉 컵이 sweet spot의 변화에도 영향을 주게 된다.

Fig. 9는 비접촉 갭의 크기를 0.6 mm으로 하고 홈이 존재하는 위치의 평면(천정에서 22 mm)에서 팁의 길이별로 홈을 통해 빠져나가는 속도 분포를 보여주고 있다. 팁의 길이에 따라서 팁 홈을 통해 토출하는 유동 패턴이 다소 상이하다. 미세한 홈의 효과는 유동의 움직임에서 일부 토출되는 것으로 알 수 있다. 단, 팁의 크기가 길어질수록 팁 하단부의 저항이 커져 홈을 통해 나가는 유동의 세기가 증가하고 있다. 이러한 부분이 내부적으로 순환의 흐름에 영향을 주게 되어 진공 흡입을 위한 주 흐름 경계가 약해진다.

Fig. 9

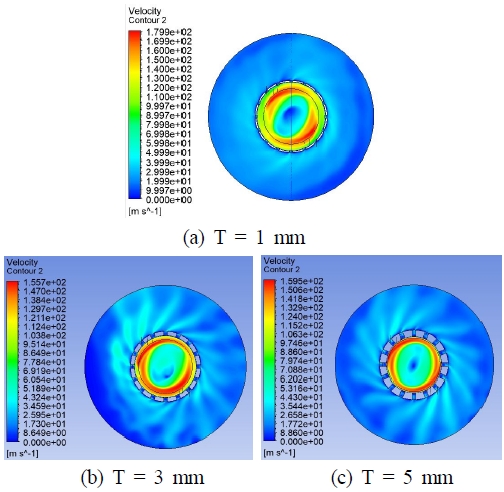
Velocity contour at the plane with the grooved passage; 0.6 mm air gap, 3.84×10-3 kg/s mass flow rate, and different tip lengths

Fig. 10은 팁 홈이 있는 경우에 갭의 크기와 팁 길이의 변화를 주었을 때 컵의 하단부에 형성되는 압력 분포를 나타내고 있다. 이 결과는 파지력을 크기로 비교한 Fig. 8과 속도의 분포를 비교한 Fig. 9의 결과를 보충하는 설명으로 팁의 길이가 길수록 상대적으로 컵 하단부에 형성되는 압력 구배의 특성에 대하여 다루고 있다. 여기서 압력 구배만으로 판단 할 수 있는 부분은 팁의 거리를 1 mm 유지할 때 벽 쪽을 제외하곤 내부에 원만한 구배를 보였다. 특히 sweet spot이라고 할 수 있는 h = 0.6 mm (T = 1 mm)에서는 가장 이상적인 분포를 보여주고 있다.

Fig. 10

Pressure distribution on the sample surface; h(gap), T(tip length), grooved tip

그리고 일반적으로 sweet 존을 벗어나는 상황에서 힘의 균형이 이루어지는 경우 팁 홈의 역할이 확연하게 비접촉 거리를 줄이는 역할을 하고 여기에 팁의 길이는 부수적으로 조정을 할 수 있는 수단이 될 수 있음을 알 수 있다. 즉, 비접촉 갭이 작을수록 반력인 양압이 증가하는 영역이 넓어지면서 진공 영역은 중앙에 집중하는 경향이 있다. 그러나 Fig. 7의 홈이 없는 경우와 달리 짧은 팁과 홈의 역할은 토출구 벽 쪽에 존재하는 반력의 영향을 줄이면서 비접촉 갭의 크기도 줄어드는 효과를 보여준다. 이는 컵 하단부에서 넓고 큰 진공 영역을 생성하기 위해서는 높은 에너지로 벽 쪽에 집중되는 스월 흐름에 부합되는 적절한 토출 면(sweet spot)을 통하여 큰 흐름 손실이 없이 빠져나가기 때문이다.

4.2.3 가이드 블록에 의한 효과

컵 내부 가이드 블록은 벽 쪽에 집중되는 스월 운동을 하단부까지 최대한 보호하고 하부에 넓은 진공 영역을 확보하면서 안정적인 파지 환경을 제공하는 데 있다. 가장 간단한 가이드 블록 형태는 컵 내부에 원통형 막대로 중앙 상부에서 아래쪽으로 이어지는 그 길이와 지름의 크기 변화로 이루어진다. 보텍스컵에서는 베르누이 형태와는 달리 내부 각운동량에 의한 유동 영역을 컵 벽 쪽으로 최대한 제한하여 진공 발생 효율이 크게 저하되지 않으면서 안정된 토출을 보여준 연구 결과가 있다^[15].

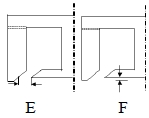
흐름의 가이드에 관한 연구로서 가이드 옆면은 Fig. 1과 Fig. 2와 같이 팁 하단부의 경사면과 같으며 ⊥자형 블록의 중앙은 2-3개의 관통로를 가지고 있는 구조를 제안하여 두 경사면 사이의 간격(E)과 바닥 부분과 가이드와의 틈새 거리(F)에 따르는 변화를 통하여 유동 패턴과 파지력을 검토하였다. 가이드 틈새는 5 mm이며, 가이드 갭은 팁 하단 기준 0, 1, 2 mm로 수준차를 두었다.

Table 3은 각각 가이드 틈새와 가이드 갭의 변화를 주었을 때 계산된 파지력을 보여주고 있다. 그 결과 가이드 갭을 줄여 스월 운동을 거의 팁 높이만큼 벽 쪽으로 최대한 억제 하는 경우보다는 가이드 높이를 팁 높이보다 더 높게 여유를 줄 때 내부 유입을 통한 순환유동 형성에 유리한 것으로 판단된다. Fig. 11은 Table 3에서 파지력이 가장 좋은 2 mm 가이드 갭의 크기를 적용했을 때 속도와 압력 단면도이다. 이 결과에서 보듯이 대체로 진공의 효과는 파지력을 늘리는 측면보다는 유동을 안정적으로 유지하는 측면에서 큰 의미를 가진다.

Table 3

Effect of guide block shape

Fig. 11

Velocity and pressure profiles; h(tip gap) = 0.6 mm, T(tip length = 1 mm) and guide gap = 2 mm

Fig. 12는 이전 결과를 토대로 유량이 3.84×10^-3 kg/s, 팁 길이가 1 mm일 때 힘의 평형상태가 팁 갭이 0.6 mm에서 유지됨을 전제로 하여 가이드 블록을 적용했을 때 Table 3과 같은 파지력이 생성되는 경우 파지 물체 표면에 형성되는 압력 분포이다. 여기서 내부 진공 균일성은 중심부에서 잘 유지되고 있음을 알 수 있으며 Fig. 10의 결과와 비교에서도 진공 영역의 확충이 개선되었다.

Fig. 12

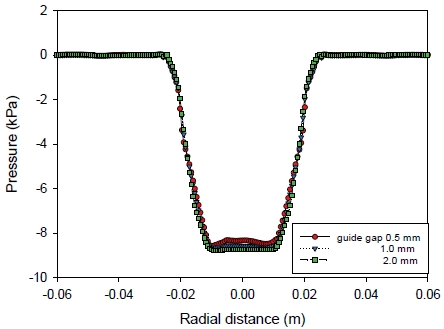
Pressure distribution on the sample surface with different gap guide and a guide clearance; h(tip gap) = 0.6 mm, T(tip length = 1 mm)

최종적으로 모따기 팁의 경사면으로 진입하기 전인 22 mm, 직전인 25 mm, 그리고 진입 후인 27 mm 평면에서 계산된 스월수로 단순 비교하기 위해 팁 갭 0.6 mm, 팁 길이 1 mm 기준으로 기본형, 팁 홈형, 가이드 블록형, All-in-one 형으로 구분하여 Table 4에 정리하였다. 공통적인 점은 토출 부위인 팁 끝단으로 접근함에 따라 스월수는 급격히 하락했으나 가이드 블록은 최대한 보텍스 흐름의 코어 부분을 보호하는 것으로 나타났다. 또한 팁 홈의 적용은 기본형에 비해 스월수 변화는 크지 않으나 실제로 반력을 완화하면서 얻는 진공 부분의 효과가 크다고 판단된다. All-in-one 형은 스월수 계산에서 특이한 부분은 없으나 끝단으로 향할수록 스월수가 급격히 하락했으며 가이드와 팁 홈의 복합 사용으로 인한 장점은 없는 것으로 보인다.

Table 4

Comparison of swirl number by the end effector

5. 결 론

보텍스 흐름을 갖는 기본 구조의 비접촉 에어 컵에서 내부 흐름을 개선하기 위해 팁 및 내부 가이드 블록의 형상 변화를 주어 최소한도 안정되는 비접촉 거리와 파지력을 획득하는 것을 계산하였다.

내경 40 mm급 기본 컵에 토출 비접촉 갭의 유효 범위 (0.3 mm ~ 0.9 mm)와 적정 사용 유량(3.89×10^-3 kg/s ~ 4.71×10^-3 kg/s) 조건에서 컵 내부 위치에 따라 계산되는 스월수 변화를 토대로 팁의 갭에 따라 획득되는 파지력 상태가 갭이 0.6~0.8 mm일 때 가장 효과적이었다.

기본형 컵에 팁의 형상(길이와 홈 설정)에 변화를 주었을 때 팁의 길이 증가는 방사 방향 토출에 대한 속도 성분과 압력에 영향을 주게 되고 파지력의 손실 없이 오히려 유효 비접촉 갭을 0.6 mm에서 0.9 mm까지 늘리는 효과를 가질 수 있었다. 또한 팁에 홈의 단면적을 전체 토출 갭의 원주상의 면적에 비해 13%를 가지는 경우에는 반대로 비접촉 갭을 0.3 mm까지 줄이면서 파지력을 향상시키는 효과를 얻었다. 추가적으로 컵 내부의 ⊥자형 가이드 블록은 5 mm 틈새와 2 mm 가이드 갭 일 때 효과적이었음을 확인했다. 틈새와 하단 갭은 어느 정도 여유를 줄 때 파지력 저하 없이 기본 보텍스 컵이 가지는 흐름의 불안정한 패턴을 안정시킨다는 기존의 결과를 재확인했다.

Acknowledgments

이 연구는 버블 생성에 중요한 스월 흐름의 성능과 연관되는 기술 내용으로 2022년 한국연구재단 개인기초연구사업(기본연구) 과제번호 2022R1F1A1071016의 연구비 지원으로 수행되었습니다.

References

• Tuleja, P., 2016, Technical Solutions of Problems in the Handling of the Object with Non-consistent Surface, American Journal of Mechanical Engineering, 4:7 400-405.
• Tiwan, A., Persson, B. N. J., 2019, Physics of Suction Cups, Soft Matter, 15 9482-9499. [https://doi.org/10.1039/C9SM01679A]
• Festo, n.d., viewed 7 November 2021, Suction Cups, <https://www.festo.com/net/SupportPortal/Files/10595/VAS_ENUS.pdf, >.
• Parker, n.d., viewed 7 November 2021, Vaccum Cups, <https://www.parkermotion.com/literature/precision_cd/CD-EM/pneumatic/cat/english/0802-A_Cups.pdf, >.
• SMC, n.d., viewed 7 November 2021, Non-contact Gripper, XT661 Series, <https://content2.smcetech.com/pdf/XT661.pdf, >.
• Lee, T. G., Yu, J. S., Jung, H. J., Kim, J.-H., Kim, J. H., 2013, Development of the Air Floating Conveyor System for the Large Glass Sheet, J. Korean Soc. Manuf. Technol. Eng., 22:4 635–642. [https://doi.org/10.7735/ksmte.2013.22.4.635]
• Liu, D., Teo, C. S., Liang, W., Tan, K. K., 2019, Soft-Acting, Noncontact Gripping Method for Ultrathin Wafers Using Distributed Bernoulli Principle, IEEE Trans. Autom. Sci. Eng., 16:2 668–677. [https://doi.org/10.1109/TASE.2018.2848635]
• Dini, G., Fantoni, G., Failli, F., 2009, Grasping Leather Plies by Bernoulli Grippers, CIRP Ann-Manuf. Technol., 58:1 21-24. [https://doi.org/10.1016/j.cirp.2009.03.076]
• Brun, X. F., Melkote, S. N., 2009, Modeling and Prediction of the Flow, Pressure, and Holding Force Generated by a Bernoulli Handling Device, J. Manuf. Sci. Eng.-Trans. ASME, 131:3 031018-1. [https://doi.org/10.1115/1.3139222]
• Li, X., Li, N., Tao, G., Liu, H., Kagawa, T., 2015, Experimental Comparison of Bernoulli Gripper and Vortex Gripper, Int. J. Precis. Eng. Manuf., 16:10 2081-2090. [https://doi.org/10.1007/s12541-015-0270-3]
• Li, X., Lio, S., Kawashima, K., Kagawa, T., 2011, Computational Fluid Dynamics Study of a Noncontact Handling Device Using Air-Swirling Flow, J. Eng. Mech., 137:6 400 - 409. [https://doi.org/10.1061/(ASCE)EM.1943-7889.0000237]
• Zhao, J., Li, X., 2016, Effect of Supply Flow Rate on Performance of Pneumatic Non-Contact Gripper Using Vortex Flow, Exp. Therm. Fluid Sci., 79 91-100. [https://doi.org/10.1016/j.expthermflusci.2016.06.020]
• Kumar, S. R., Karthick, P. A., Boovendravarman, S., Raghul, K. S., Thiyagu, S., 2020, Characteristics of Contactless Swirl Vane Gripper by Investigating the Negative Pressure and Clearance, Materials Today: Proceedings, 33:1 270-274. [https://doi.org/10.1016/j.matpr.2020.04.044]
• Li, X., Kagawa, T., 2013, Development of a New Noncontact Gripper Using Swirl Vanes, Robot. Comput.-Integr. Manuf., 29:1 63-70. [https://doi.org/10.1016/j.rcim.2012.07.002]
• Kim, J. H., Sung J., 2019, Influence of Air Head Shape on Lifting Force and Stability of Swirl Flow in a Vortex-Type Non-Contact Gripper, J. Korean Soc. Manuf. Technol. Eng., 28:4 224-231. [https://doi.org/10.7735/ksmte.2019.28.4.224]
• Kim, J. H., Lee, S., 2015, Configuration of Noncontact Grip System for Carrying Large Flat Sheets Using Vacuum Air Heads, Journal of Tribology, 137:4 041103. [https://doi.org/10.1115/1.4030710]
• Lee, Y. H., Kim, J. H., Sung, J., 2021, Enhanced Non-Contact Grip Force and Swirl Stability by a Combined Venturi–Vortex Air Head, Materials, 14:23 7123. [https://doi.org/10.3390/ma14237123]
• Vaidya, H. A., Ertunç¸, ö., Genç, B., Beyer, F., Köksoy, ç., Delgado, A., 2011, Numerical Simulations of Swirling Pipe Flows- Decay of Swirl and Occurrence of Vortex Structures, 13th European Turbulence Conference (ETC13) J. Phys.: Conf. Ser., 318 062022. [https://doi.org/10.1088/1742-6596/318/6/062022]
• Rocklage-Marliani, G., Schmidts¸, M., Vasanta Ram, V. I., 2003, Three-Dimensional Laser-Doppler Velocimeter Measurements in Swirling Turbulent Pipe Flow, Flow Turbul. Combust., 70 43-67. [https://doi.org/10.1023/B:APPL.0000004913.82057.81]