절삭 시뮬레이션에 사용되는 구성방정식 종류별 절삭력 예측

2.1 구성방정식

구성방정식은 절삭 및 소성 시뮬레이션에서 사용되는 물성으로 F는 가공 경화항(ε), G는 변형률 속도 경화항($$ \dot{\epsilon }$$), T는 열연화항(M)의 함수로 구성되어 있다. 이를 식(1)에 나타내었다.

각 항의 구성에 따라 다양한 방정식으로 구성되며 식(2)는 Johnson-Cook 구성방정식으로 (A + Bεⁿ)는 재료의 변형률 경화를 나타내고 있으며, A는 초기항복응력, B는 경화상수, n은 경화지수, ε은 변형률을 나타낸다.

($$ 1+C\mathrm{l}\mathrm{n}\frac{\dot{\epsilon }}{{\dot{\epsilon }}_0}$$)는 변형률 속도 경화를 나타내며, $$ \dot{\epsilon }$$ 는 변형률 속도, $$ {\dot{\epsilon }}_0$$는 단위 변형률 속도 (1 mm/sec)를 나타낸다. 각각 변형률 속도가 sec-1인 경우의 응력-변형률 선도를 Ludwick의 식으로 나타내었을 경우에 해당하는 상수들이다. 변형률속도 경화계수 C를 구하기 위하여 초기항복응력의 변화를 변형률 속도에 따라 나타낸 Log선도를 이용하게 된다.

이 때 C는 열연화 현상을 배제하고 등온 변형과정일 때 얻어지게 되므로 초기항복이 발생할 때 구한다. m은 열연화계수이다.

식(3)은 S-K 구성방정식으로 변형률 속도항의 계수값 E에 의하여 고속에서 응력값이 증가하는 현상을 기술할 수 있는 특징을 가지고 있다 σ는 유동응력, A는 항복강도, B와 C는 가공경화상수, D는 변형률 속도 경화상수, E는 고속에서 응력값이 증가하는 것을 표현하는 변형률 속도 제어상수, m은 열연화계수, ε은 유효소성변형률, $$ \dot{\epsilon }$$은 변형률 속도, $$ {\dot{\epsilon }}_0$$는 기준 변형률 속도, T는 온도, T_melt는 재료의 용융온도, T_ref는 실험온도를 의미한다.

S-K 구성방정식 계수값을 획득하기 위한 데이터는 상온에서 다양한 속도를 변화시키면서 응력–변형률 선도를 획득하고 이를 진응력-진변형률 선도로 변환 후 방정식의 계수값 선정에 적용한다. 그리고 고온에서는 충격속도를 일정하게 유지하고 온도 변화를 주어 진응력-진변형률 선도를 획득하여 적용한다.

식(4), (5), (6)은 Power-Law 구성방정식의 각항의 식을 나타내었다. 식(4)의 σ₀은 초기항복응력, ε_cut는 컷오프변형, 1/n은 변형경화지수를 나타내었다. 식(5)의 $$ \dot{\epsilon }$$ 는 변형률 속도로 낮은 변형률 감도와 높은 변형률 감도 사이의 전환에서 발생하는 변형률, $$ {\dot{\epsilon }}_0$$는 단위 변형률속도, m₁은 낮은변형률 감도계수이며, m₂는 높은 변형률 감도계수이다. 식(6)의 c₀∼c₅는 다항식 피팅에 대한 계수, T는 온도, T_cut은 선형차단온도 T_melt는 용융온도를 나타내고 있다.

구성방정식의 계수는 준정적 시험과 SHPB 시험에서 획득한 응력-변형률 커브 데이터를 이용하여 구성방정식 계수값을 통계프로그램 오리진 또는 매트랩과 같은 프로그램에서 비선형 커브 피팅을 통하여 획득할 수 있다.

2.2 절삭조건 및 실험

2차원 절삭실험은 구성방정식을 적용한 시뮬레이션 결과값을 검증하기 위하여 절삭조건에 따른 절삭력을 측정하였다. 최고 3500 rpm의 주축회전속도를 가지는 CNC선반을 이용하였다. 주축에 2차원 절삭 시편을 장착하고 공구메거진에 공구동력계를 부착하였다. 그리고 공구동력계 상부에 공구 홀더 및 공구를 장착하여 절삭력을 획득하였다.

Fig. 1의 (a)는 시편 및 절삭력 측정 장비가 부착되어 있는 그림을 나타내었다. 시편은 회전하고 공구메거진이 부착되어있는 공구가 직선적으로 이동하여 시편에 접근하여 2차원 절삭실험으로 절삭력을 측정한다. Fig. 1의 (b)는 2차원 절삭실험에 사용된 시편을 나타내고 있다. 시편은 주축에 장착되고 절삭실험 부위는 디스크 형태로 직경 ∅50 mm, 두께는 3 mm로 제작하였다. 시편의 재료는 Al7075 재료를 사용하였으며 공구는 대구텍 TPGN220404 초경공구를 사용하였다.

Fig. 1

Specimen and test equipment for two-dimensional cutting experiments

Table 1은 구성방정식을 적용한 시뮬레이션의 결과값을 검증하기 위한 조건으로 절삭속도와 이송의 변화를 나타내었다. 절삭조건은 공구회사에서 제시한 절삭조건을 절삭실험에서 적용하였다.

Table 1

Cutting conditions for comparison of cutting forces

2.3 절삭시뮬레이션

구성방정식을 적용하기 위한 시뮬레이션은 AdvantEdge FEM 7.4 버전으로 2차원 절삭 가공에서 평면변형률의 열 구조 연성 유한요소 모델을 생성하여 사용한다. 공작물은 탄소성 거동에서 변형률, 변형률 속도 및 온도에 의한 유동응력에 의해 결정된다고 가정하였다. 본 연구에서 사용한 소프트웨어는 절삭 전용 시뮬레이션 프로그램으로 절삭조건인 절삭속도, 절입량, 이송속도를 입력하여 절삭력, 칩형상, 절삭온도 등을 절삭에서 발생하는 여러 가지 물리적 데이터를 예측할 수 있다. 절삭 시뮬레이션에서 절삭력에 영향을 미치는 조건은 다양하다. 절삭조건인 이송속도, 절삭속도, 절입량과 절삭 재료 및 절삭 공구 재료 등이 절삭력에 영향을 미친다. 그리고 절삭 공구의 각도, 마찰계수 및 격자 크기 등 기하학적인 부분 또한 절삭력에 영향을 미친다.

본 연구에서 사용된 절삭 시뮬레이션의 일반적인 공정은 재료시험으로 물성 데이터를 확보하고 절삭조건을 입력한 후 시뮬레이션을 수행한 후 TECPLOT으로 절삭에서 발생하는 물리적 데이터를 확인할 수 있다. 그리고 사용자 물성 모델인 구성방정식 적용을 위해서는 포트란을 이용하여 구성방정식을 적용하기 위한 프로그램을 코딩하고 DLL 파일을 생성하고 솔버에 적용한다. 그리고 소재 물성값은 SHPB 실험을 통하여 획득한 데이터를 이용하여 계수값을 획득하고 이를 절삭 재료의 물성을 적용한 후 기본조건인 절삭조건을 입력하고 시뮬레이션을 실행한 후 물리적 데이터를 확인할 수 있다.

3.1 구성방정식 계수 결정

본 연구에서는 Al7075 재료를 사용하였으며 구성방정식의 계수값은 SHPB 시험을 통하여 획득한 결과값을 이용하여 기준 변형률로 변형률 속도에 따른 응력-변형률 선도를 나타낸다. 본 연구에서는 상온과 고온의 SHPB실험을 통하여 획득한 그래프를 이용하여 오리진의 커브피팅으로 계수값을 획득하였다.

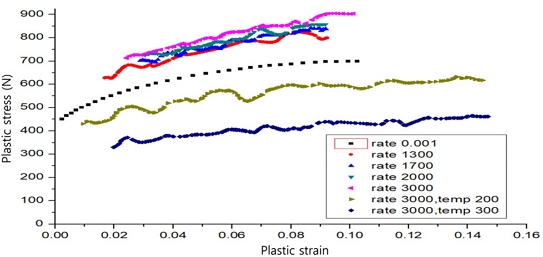
Fig. 2는 실험 조건별 소성 진응력-진변형률 선도를 나타내고 있다. 속도가 0.001 s^-1의 저속구간은 만능시험기를 이용하여 압축실험을 수행하여 데이터를 획득하였다. 그리고 고속구간은 1300 s^-1, 1700 s^-1, 2000 s^-1, 3000 s^-1조건 고온구간은 고속구간을 3000 s^-1로 고정하고 200℃, 300℃에서 SHPB 압축실험을 통하여 응력-변형률 곡선을 획득하였다. 그리고 획득한 응력-변형률 선도를 진응력-진변형률 선도로 변환하였다. 진응력-진변형률 선도에서 탄성구간을 제외하면 소성진응력-진변형률 곡선이 완성된다. 이를 이용하여 기준 변형률 속도를 0.001 s^-1으로 비선형 커브 피팅으로 계수값을 구하였다. Table 2와 Table 3은 Johnson-Cook 구성방정식과 S-K 구성방정식의 계수값을 나타내었다.

Fig. 2

Change of plastic stress-plastic strain according to the speed change obtained by SHPB experiment

Table 2

Johnson-Cook constitutive equation parameters of Al7075

Table 3

S-K constitutive equation parameters of Al7075

3.2 구성방정식 계수 검증

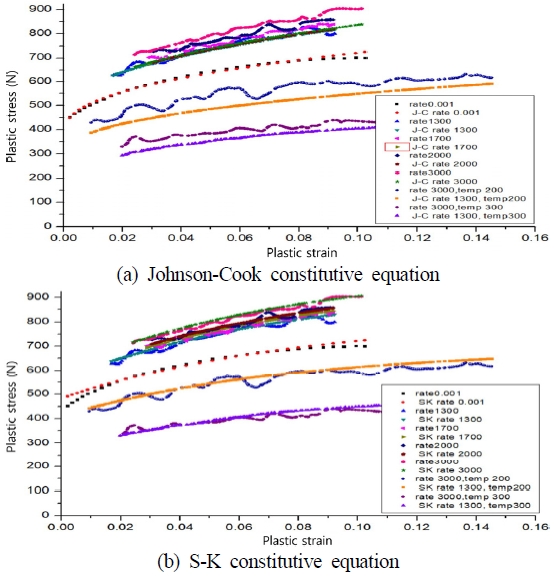
구성방정식의 계수 검증은 결정된 계수를 수식에 적용하고 이를 SHPB 실험에서 얻어진 실험 데이터와 비교하였다. Fig. 3은 결정된 구성방정식이 변형률 속도 및 온도에 변화에 따른 SHPB 실험 결과와 구성방정식으로 예측한 결과를 비교하여 나타내었다. Fig. 3의 (a)는 Johnson-Cook 구성방정식과 실험 결과를 비교한 그래프로 저속 변형률 속도(0.001 s^-1)에서 낮은 변형률 에서는 정확하게 응력값을 예측하고 있으나 변형률이 0.08이상에서는 구성방정식으로 예측한 값이 높아졌다. 그리고 고속에서는 변형률 속도가 증가하더라도 하나의 값으로 예측하고 있으며 고온에서는 실험값보다 낮은 응력값으로 예측되었다. Fig. 3의 (b)는 S-K 구성방정식과 실험 결과를 비교한 그래프로 낮은 변형률 속도(0.001 s^-1)에는 Johnson-Cook 구성방정식과 동일하게 변화하였으나 변형률 속도가 고속일 때는 구간별로 구분할 수 있을 정도로 응력값을 예측하고 고온에서는 Johnson-Cook 구성방정식보다 S-K 구성방정식이 실험데이터와 비슷하게 응력값을 예측하고 있다.

Fig. 3

Comparison of the constitutive equation by the determined coefficient and the SHPB experimental data

4.1 절삭실험으로 획득한 절삭력

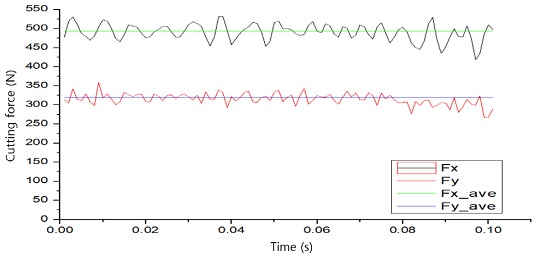
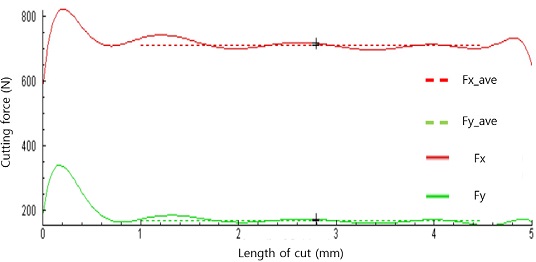
절삭실험과 시뮬레이션의 결과 데이터를 비교 분석하기 위하여 절삭실험으로 획득한 절삭력을 기준으로 하나의 값으로 결정하기 위하여 절삭력을 평균하였다. Fig. 4는 case 02인 절삭속도 200 m/min, 이송 0.2 mm/rev 조건에서 절삭실험으로획득한 절삭력을 나타내고 있으며 주분력(tangential force)을 Fx로 나타내었으며 배분력(radial force)을 Fy로 나타내었다. 그리고 주분력의 평균값을 Fx_ave, 배분력의 평균값을 Fy_ave로 나타내었다. 절삭력을 평균값으로 나타낸 이유는 절삭 시뮬레이션에서 얻어진 절삭력과 비교하기 위하여 절삭력을 평균값으로 결정하였다.

Fig. 4

Fx and Fy cutting forces by cutting conditions

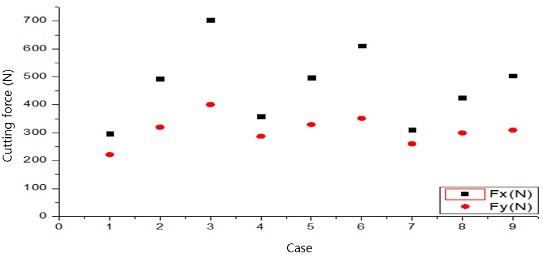
Table 4는 절삭실험에서 얻은 절삭조건별 평균 주분력과 평균배분력을 나타내었다. 절삭속도를 200 m/min으로 고정하고 이송을 0.1 mm/rev, 0.2 mm/rev, 0.3 mm/rev으로 변화하면 평균 주분력은 296.145 N, 358.171 N, 309.644 N으로 변화하였다. 그리고 절삭속도를 300 m/min으로 고정하고 이송을 변화하면 평균 주분력은 358.171 N, 496.281 N, 611.145 N으로 변화하였다. 절삭속도를 400 m/min으로 고정하고 이송을 변화하면 평균 주분력은 309.644 N, 424.687 N, 503.916 N으로 변화하였다. 절삭속도를 고정하고 이송이 변화할 때는 평균 주분력이 직선적으로 증가하였다. 평균 배분력은 절삭속도를 200 m/min으로 고정하고 이송을 0.1 mm/rev, 0.2 mm/rev, 0.3 mm/rev으로 변화하면 평균 주분력은 221.511 N, 319.553 N, 401.052 N으로 변화하였다. 그리고 절삭속도를 300 m/min으로 고정하고 이송을 변화하면 평균 주분력은 287.203 N, 329.140 N, 351.155 N으로 변화하였다. 절삭속도를 400 m/min으로 고정하고 이송을 변화하면 평균 주분력은 260.637 N, 299.172 N, 309.312 N으로 변화하였다. 평균 배분력은 주분력 변화보다 절삭력 증가폭이 낮은 것을 확인하였다. 배분력은 절삭속도 200 m/min에서 이송을 증가시키면 절삭력이 증가하고 절삭속도 300 m/min, 400 m/min에서는 절삭력이 낮게 증가하였다. 이송속도를 0.1 mm/rev으로 고정하고 절삭속도를 200 m/min, 300 m/min, 400 m/min으로 변화시키면 평균 주분력은 296.145 N, 358.171 N, 309.644 N으로 변화하였다. 이송속도를 0.2 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 493.007 N, 496.281 N, 424.987 N으로 변화하였다. 이송속도를 0.3 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 703.739 N, 611.145 N, 503.916 N으로 변화하였다. 이송을 0.1 mm/rev, 0.2 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력의 변화가 적었으니 이송을 0.3 mm/rev으로 고정하고 절삭속도를 변화시키면 주분력이 낮아졌다.

Table 4

Two-dimensional cutting force by cutting conditions

4.2 구성방정식 변화에 따른 시뮬레이션 절삭력

절삭 시뮬레이션은 세 가지 구성방정식을 적용하여 절삭력을 분석하고 적용 가능한 구성방정식을 결정하였다.

Fig. 5

Fx and Fy cutting forces by cutting conditions

Fig. 6은 case 02인 절삭속도 200 m/min, 이송 0.2 mm/rev 조건에서 S-K 구성방정식을 적용한 절삭 시뮬레이션에서 획득한 절삭력을 나타내었다. 주분력을 Fx로 나타내었으며 배분력을 Fy로 나타내었다. 그리고 주분력의 평균값을 Fx_ave, 배분력의 평균값을 Fy_ave로 나타내었다. 절삭실험 데이터와 비교분석을 위하여 절삭력을 평균하여 나타내었다.

Fig. 6

Fx and Fy simulation cutting forces by cutting conditions

Table 5는 Johnson-Cook 구성방정식을 적용한 시뮬레이션의 절삭조건별 평균 주분력과 평균 배분력을 나타내고 있다. 절삭속도를 200 m/min으로 고정하고 이송을 0.1 mm/rev, 0.2 mm/rev, 0.3 mm/rev으로 변화하면 평균 주분력은 380.385 N, 739.582 N, 1075.02 N으로 변화하였으며 평균 배분력은 181.986 N, 338.414 N, 481.994 N으로 변화하였다. 그리고 절삭속도를 300 m/min으로 고정하고 이송을 변화하면 주분력은 381.062 N, 744.954 N, 1079.230 N으로 변화하였으며 평균 배분력은 182.231 N, 341.624 N, 481.754 N으로 변화하였다. 절삭속도를 400 m/min으로 고정하고 이송을 변화하면 주분력은 379.869 N, 741.610 N, 1080.300 N으로 변화하였으며 평균 배분력은 181.178 N, 338.939 N, 482.962 N으로 변화하였다. 이송속도를 0.1 mm/rev으로 고정하고 절삭속도를 200 m/min, 300 m/min, 400 m/min으로 변화시키면 평균 주분력은 380.385 N, 381.062 N, 379.869 N으로 변화하였으며 평균 배분력은 181.986 N, 182.231 N, 181.178 N으로 변화하였다. 이송속도를 0.2 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 739.582 N, 744.954 N, 741.610 N으로 변화하였으며, 평균 배분력은 338.414 N, 341.624 N, 338.939 N으로 변화하였다. 이송속도를 0.3 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 1075.020 N, 1079.230 N, 1080.300 N으로 변화하였으며, 평균 배분력은 481.994 N, 481.754 N, 482.962 N으로 변화하였다.

Table 5

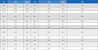
Simulation cutting force by applying Johnson-Cook constitutive equation by changing cutting conditions

절삭속도를 고정하고 이송속도를 증가시키면 평균 주분력과 평균 배분력 모두 직선적으로 증가하고 있으며 평균 주분력 증가량이 평균 배분력 증가량 보다 높게 나타났다.

Table 6은 S-K 구성방정식을 적용한 시뮬레이의 절삭조건별 주분력과 배분력을 나타내고 있다. 절삭속도를 200 m/min으로 고정하고 이송을 0.1 mm/rev, 0.2 mm/rev, 0.3 mm/rev으로 변화하면 평균 주분력은 281.736 N, 514.795 N, 737.182 N으로 변화하였으며 평균 배분력은 130.579 N, 184.842 N, 202.718 N으로 변화하였다. 그리고 절삭속도를 300 m/min으로 고정하고 이송을 변화하면 평균 주분력은 272.611 N, 511.096 N, 749.772 N으로 변화하였으며 평균 배분력은 120.289 N, 164.682 N, 178.769 N으로 변화하였다. 절삭속도를 400 m/min으로 고정하고 이송을 변화하면 평균 주분력은 269.481 N, 513.977 N, 711.080 N으로 변화하였으며 평균 배분력은 113.839 N, 155.171 N, 165.766 N으로 변화하였다. 절삭속도를 고정하고 이송속도를 증가시키면 평균 주분력 변화는 Johnson-Cook과 비슷한 경향성을 보였으나 전체 평균 주분력은 낮게 나타났다.

Table 6

Cutting force of cutting simulation by S-K constitutive equation

이송속도를 0.1 mm/rev으로 고정하고 절삭속도를 200 m/min, 300 m/min, 400 m/min으로 변화시키면 평균 주분력은 281.736 N, 272.611 N, 269.481 N으로 변화하였으며 평균 배분력은 130.579 N, 120.682 N, 113.839 N으로 변화하였다. 이송속도를 0.2 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 514.795 N, 511.096 N, 513.977 N으로 변화하였으며, 평균 배분력은 184.842 N, 164.682 N, 155.171 N으로 변화하였다. 이송속도를 0.3 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 737.182 N, 749.772 N, 711.080 N으로 변화하였으며, 평균 배분력은 202.718 N, 178.769 N, 165.766 N으로 변화하였다.

Table 7은 Power-Law 구성방정식을 적용한 시뮬레이션의 절삭조건별 주분력과 배분력을 나타내고 있다. 절삭속도를 200 m/min으로 고정하고 이송을 0.1 mm/rev, 0.2 mm/rev, 0.3 mm/rev으로 변화하면 평균 주분력은 276.335 N, 519.201 N, 741.255 N으로 변화하였으며 평균 배분력은 88.329 N, 136.312 N, 180.231 N으로 변화하였다. 그리고 절삭속도를 300 m/min으로 고정하고 이송을 변화하면 평균 주분력은 277.4 N, 520.637 N, 744.042 N으로 변화하였으며 평균 배분력은 87.571 N, 135.494 N, 181.955 N으로 변화하였다. 절삭속도를 400 m/min으로 고정하고 이송을 변화하면 평균 주분력은 278.979 N, 520.309 N, 745.138 N으로 변화하였으며 평균 배분력은 88.754 N, 137.989 N, 182.184 N으로 변화하였다.

Table 7

Cutting force of cutting simulation by Power-Law constitutive equation

이송속도를 0.1 mm/rev으로 고정하고 절삭속도를 200 m/min, 300 m/min, 400 m/min으로 변화시키면 평균 주분력은 276.335 N, 277.400 N, 278.979 N으로 변화하였으며 평균 배분력은 88.329 N, 87.571 N, 88.754 N으로 변화하였다. 이송속도를 0.2 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 519.201 N, 520.637 N, 520.309 N으로 변화하였으며, 평균 배분력은 136.312 N, 135.494 N, 137.989 N으로 변화하였다. 이송속도를 0.3 mm/rev으로 고정하고 절삭속도를 변화시키면 평균 주분력은 741.255 N, 744.255 N, 745.138 N으로 변화하였으며, 평균 배분력은 180.231 N, 181.955 N, 182.184 N으로 변화하였다. 절삭속도를 고정하고 이송속도를 증가시키면 평균 주분력 변화는 S-K 구성방정식 물성에서 얻어진 절삭력과 비슷한 절삭력과 경향성을 보였다.

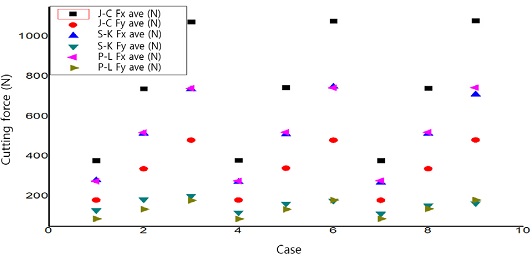
Fig. 7은 절삭조건별 절삭시뮬레이션에 적용된 구성방정식의 변화에 따른 평균 주분력과 평균 배분력의 변화를 나타내었다. S-K와 Power-Law 구성방정식을 물성으로 사용하여 얻은 평균 절삭력은 비슷한 경향성을 얻었으나 Johnson-Cook 구성방정식을 물성으로 사용하여 얻어진 평균 절삭력은 S-K와 Power-Law 구성방정식을 물성으로 획득한 절삭력보다 높게 나타났다.

Fig. 7

Changes in cutting force to changes in the constitutive equation(cutting condition)

4.3 절삭실험과 시뮬레이션에서 획득한 절삭력 비교

절삭실험을 기준으로 구성방정식을 물성으로 적용하여 얻어진 평균 절삭력의 변화를 비교 분석하였다. Table 8은 절삭실험으로 얻은 평균 절삭력을 기준으로 시뮬레이션에서 얻어진 절삭력과의 오차를 나타내고 있다. Johnson-Cook 구성방 정식에서 얻어진 최대 평균 주분력오차는 case 9에서 나타났다. 평균 주분력은 최대 576 N의 오차를 나타내었으며 평균 배분력은 최대 173.65 N의 오차를 나타내었다. 그리고 S-K와 Power-Law 구성방정식에서 얻어진 평균 주분력 오차는 case 9에서 207.16 N과 241.22 N의 오차를 보였으며 평균 배분력은 case 3에서 -198.33 N과 -220.82 N의 오차를 나타내었다.

Table 8

Simulation cutting force and cutting experiment cutting force error by constitutive equations as material properties

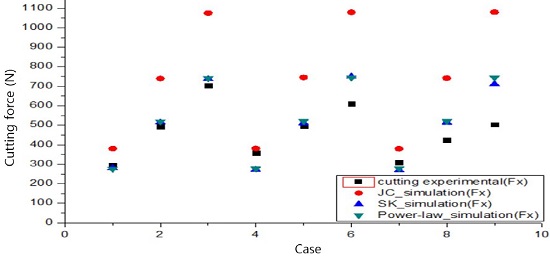
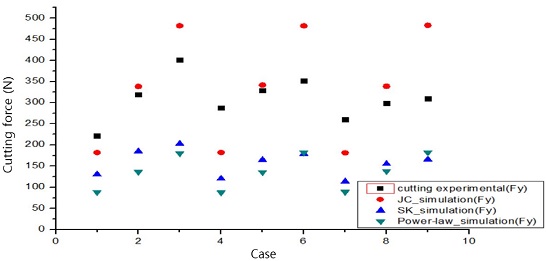
Fig. 8과 Fig. 9는 절삭실험과 시뮬레이션에서 얻은 평균 주분력과 평균 배분력을 나타내었다. 평균 주분력의 결과는 Johnson- Cook 구성방정식을 적용한 시뮬레이션에서 가장 큰 오차를 나타내고 있으며 S-K와 Power-Law 구성방정식을 적용한 시뮬레이션으로 예측한 절삭력은 비슷한 경향성을 보였다. 평균 배분력은 S-K와 Power-Law 구성방정식을 적용한 시뮬레이션에서 예측한 결과보다 Johnson-Cook 구성방정식으로 예측한 결과가 평균 배분력 예측에 적정할 것으로 판단된다. 시뮬레이션에서 절삭력을 예측할 때는 절삭에 많은 영향을 주는 주분력을 기준으로 절삭력을 예측하기 때문에 S-K 구성방정식으로 절삭력을 예측하는 것이 좋을 것으로 판단된다.

Fig. 8

Comparison of Fx force obtained from cutting experimentals and simulations

Fig. 9

Comparison of Fy force obtained from cutting experimentals and simulations

4.4 절삭실험과 시뮬레이션에서 획득한 절삭칩 비교

절삭 칩형상을 확인하는 이유는 절삭칩의 형상이 절삭에서 표면 형상에 영향을 미치는 것과 절삭력에 영향을 확인한다.

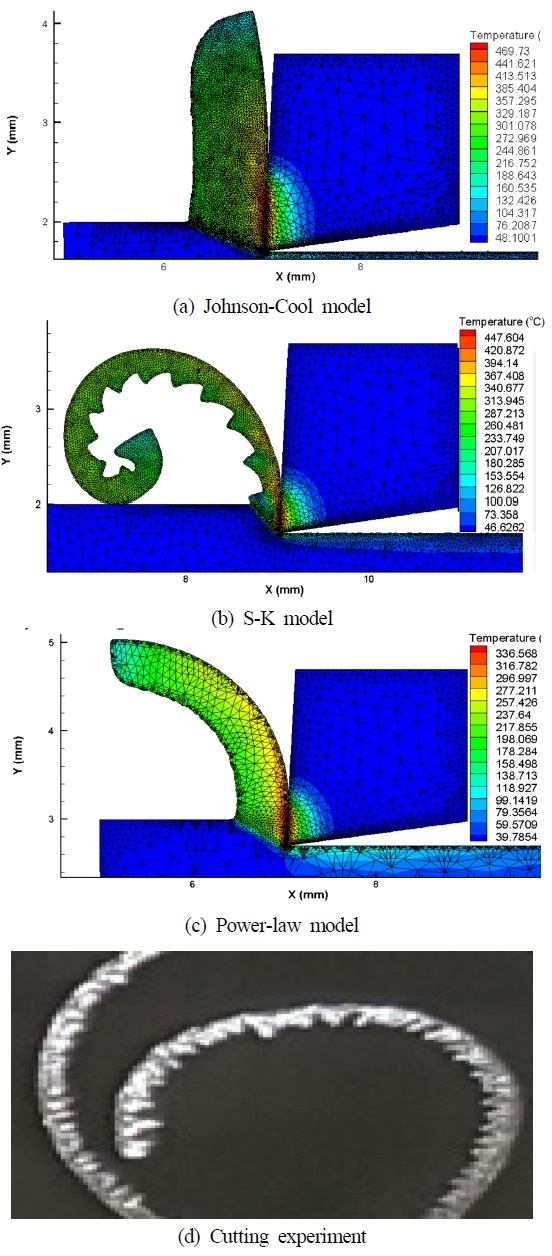
Fig. 10은 case 09에서 절삭실험과 시뮬레이션에서 발생하는 칩형상을 나타내었다. Fig. 10의 (a)는 Johnson-Cook 구성방정식을 적용한 시뮬레이션에서 얻어진 칩형상 유동형 칩이 발생하는 것을 확인하였으며 칩 두께가 두꺼워지면서 전단각이 낮아지고 이로 인하여 절삭력에 영향을 미치는 것을 확인하였다. Fig. 10의 (b)는 S-K 구성방정식을 적용한 시뮬레이션에서 얻어진 칩형상으로 Johnson-Cook 구성방정식과 다르게 톱니형 칩의 형태를 나타내고 있는 것을 확인하였다. Fig. 10의 (c)는 Power-Law 방정식을 적용한 시뮬레이션에서 얻어진 칩형상으로 Johnson-Cook 구성방정식과 동일하게 유동형 칩형태를 나타내고 있으나 전단각이 높아지면서 절삭력이 낮아지는 것을 알 수 있었다. Fig. 10의 (d)는 절삭실험으로 얻어진 칩형상으로 전단형 칩의 형상을 하고 있었다 그래서 칩형상을 예측할 때는 S-K 구성방정식으로 절삭칩을 예측하는 것이 좋을 것으로 판단된다.

Fig. 10

Chip formation in case 09 condition