국부 불량형상의 영향을 받지 않는 3D 곡선의 스트레칭 정합
Abstract
In the case of shoe midsoles produced through a foam mold process, shape differences occur even between the same parts owing to the characteristics of the production method. Thus, the automation of shoe manufacturing is hindered. To solve this problem and register, the non-rigid registration that allows stretching can be used. To implement the matching algorithm, approximate matching using the second moment of inertia and precise matching using MBA(multi-level B-spline approximation) are used. In particular, we propose the method of repeatedly performing low-resolution MBA to minimize the impact of noise. Finally, the registration error and required time are measured to determine whether the algorithm is suitable for use in real-time processes.
Keywords:
Registration, Stretching, Minor defect, Shoe midsole, 3D scan, Automated process1. 서 론
정합(registration)이란 유사한 2개의 형상을 오차가 가장 작도록 위치시키는 작업을 말한다[1-3]. 자동화 공정에서 정합은 가공하기 위해 투입된 제품을 스캔한 후 여기에 미리 학습된 형상을 최적의 위치로 이동시켜 가공경로를 획득하는 데 사용될 수 있다. 이 경우 정합의 정확도와 성능에 따라 가공 품질이 좌우될 수 있다.
때로는 강체 이동 외에 형상의 변형(streching)이 허용되어야 할 때도 있다. 발포 금형 공정으로 생산되는 신발 중창(shoe midsole)의 경우 재료의 특성으로 성형수축이 발생하여 같은 금형에서 나온 제품도 제품마다 약간의 뒤틀림이 있어 형상에 차이가 발생한다. 이러한 제품의 가공데이터를 얻고자 할 때, 파트를 스캔하고 스캔 된 데이터에 미리 학습된 형상데이터를 정합하게 되는데 이때 스트레칭(stretching)을 허용한 비강체(non-rigid) 정합[4,5]을 사용하게 된다. 한편 신발 제품의 특성 상 한 가지 디자인에 20여개 이상의 사이즈가 존재하는 것도 스트레칭을 허용해야 하는 이유가 된다. 미리 준비하는 티칭모델을 사이즈대로 모두 마련하기 어렵기 때문이다. 위와 같은 이유로 제품과 티칭모델 사이에 근본적인 차이가 있으므로 스트레칭이 허용되지 않으면 아무리 최적의 정합이 이루어져도 가공경로에 그만큼의 오차가 발생하게 된다.
하지만 스트레칭을 제한없이 허용하게 된다면 정합도는 높아지겠으나 티칭모델이 원래의 형태를 잃게 되고 특히 스캔모델에 노이즈가 있을 경우 그것마저 모두 추종해버리는 불합리가 발생할 수 있다. 본 연구에서는 이러한 단점을 보완하여 인라인 공정에 적용할 수 있는 노이즈의 영향을 최소화하는 3차원 곡선 데이터의 비강체 정합 알고리즘을 제안한다. 본 연구에서 제안하는 정합방법은 ① 전반적인 형태(look-see)는 추종하도록 변형이 일어나지만 ② 지역적인 노이즈는 무시하게 되는, 서로 모순되는 요구를 적절한 선에서 만족시키는 특징을 가진다.
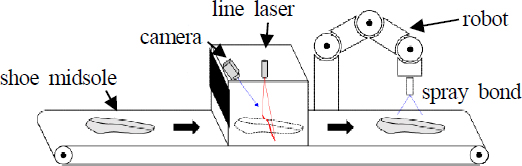
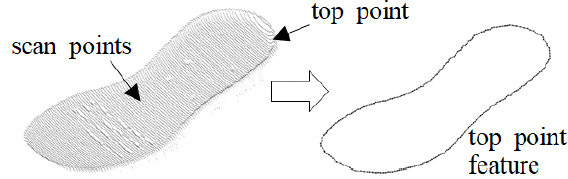
정합 실험 대상으로 Fig. 1과 같은 인라인 공정에서 획득된 중창의 스캔 데이터를 사용한다. 컨베이어 벨트에 투입된 신발 중창을 라인 단위의 점(point)으로 위쪽에서 스캔하여 데이터를 획득하고, 획득한 데이터에서 가장자리의 높은 점(top point)을 특징점으로 추출한 뒤 이들 특징점을 연결하는 3차원 곡선(top line)을 생성한다. 그리고 추출된 특징 곡선에 미리 획득한 템플릿 데이터를 정합한다. Fig. 2는 스캔 데이터와 여기서 추출된 특징 곡선의 예를 보여준다.
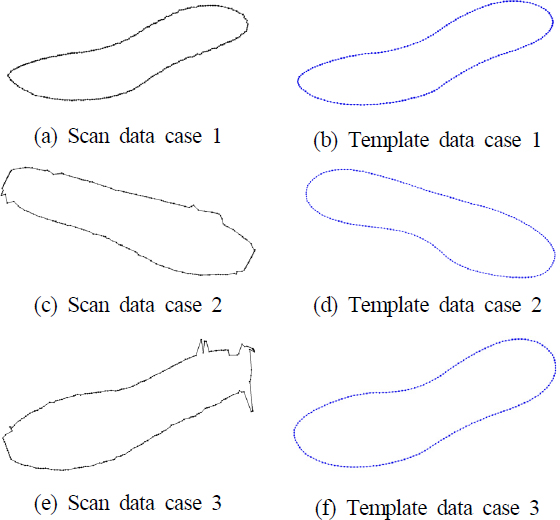
한편 Fig. 3은 스캔 데이터와 템플릿 데이터의 3가지 예를 보여준다. 그림에서 (a)는 노이즈가 거의 없이 스캔된 경우이고 (c)는 앞뒤에 약간의 노이즈가 발생한 경우이며 (e)는 뒤꿈치에 노이즈를 크게 갖고 있는 경우이다. 본 논문에서는 정합방법에 대해 먼저 설명하고 그림의 세 가지 경우에 이 방법을 적용한 결과를 설명하겠다.
2. 3차원 곡선 데이터의 대략적 정합
정합은 두 단계로 이뤄지게 되는데 이는 대략적 정합(rough registration)과 정밀 정합(fine registration)이다[6]. 이때 대략적 정합은 형상 데이터의 위치와 자세를 유사하도록 크게 움직여 대략적으로 위치시키는 과정이다. 이후에 미세 오차를 줄이면서 최적의 위치로 옮기는 정밀한 정합이 수행된다. 정밀 정합에는 여러 방법이 있지만 이들의 공통점은 근접한 점까지의 거리를 최소화시키는 시도를 한다는 것이다. 이런 정밀정합은 초기 조건에 따라 시간과 정밀도의 성능이 달라지므로, 양질의 대략적 정합 결과가 얻어질 필요가 있다.
대략적 정합은 보통, 정형화된 방법이 없고 주어진 상황마다 다른 접근방법이 사용된다. 주로 사용되는 아이디어로는, 정의된 마커를 통해 정합하는 방법, 특징 점을 사용하는 방법, 문제의 상황을 활용하는 방법 등이 있다. 본 연구에서는 제품형상의 스캔이 항상 정해진 방법으로 수행된다고 가정한다. 즉, 컨베이어에 투입될 때 중창 바닥이 아래를 향하고, 코(toe)가 앞쪽이 되도록 길이 방향으로 투입되고, 이송 중 라인레이저로 스캔되는 것이다. 이 상황을 대략적 정합의 전략에 이용한다.
이렇게 스캔이 되면 획득한 특징점들은 z축 방향으로 큰 차이가 없어 2.5차원 데이터로 취급할 수 있다. 따라서 분포되는 형태가 평면에 존재하는 것과 유사하므로 xy평면에 투영하여 그 위치와 자세를 찾으면 xy평면에서의 정합이 수행될 수 있다. 이후 높이 방향(z 방향)은 특징점들의 평균 위치로 조정하여 대략적 정합을 수행할 수 있다.
2.1 경계 상자(bounding box)를 이용한 대략적 정합
2차원에 투영된 곡선 데이터의 대략적 정합 방법 중 대표적인 것으로 경계 상자(bounding box) 방법이 있다. 경계 상자란 주어진 데이터를 둘러싸는 최소크기의 직사각형을 말하는데 통상 각 변이 x축 혹은 y축과 평행하지 않게 얻어진다. 경계 상자에 의한 대략적 정합은 다음과 같이 수행된다. 먼저 각 데이터에 대해 포함하는 경계 상자를 각각 찾는다. 그리고 경계 상자의 중심이 일치하고 장축과 단축이 나란히 되도록 옮긴다. 경계 상자는 다수의 점에 대해 상당히 신속하게 찾아지고 직사각형끼리의 정렬은 단순한 계산이므로 속도가 빠르다는 장점이 있어 여러 상황에서 자주 사용된다. 하지만 경계 상자는 작은 노이즈에도 크게 흔들릴 수 있다는 단점이 있다.
2.2 단면 이차 모멘트를 사용한 대략적 정합
본 논문에서는 노이즈의 영향을 최소화하는 대략적 정합을 구현하기 위해 단면 이차 모멘트를 사용한 정합 방법을 제안한다. 이 방법은 두 데이터의 무게 중심을 일치시킨 뒤 단면 이차 모멘트를 통해 얻은 주축을 정렬시켜 정합을 수행한다.
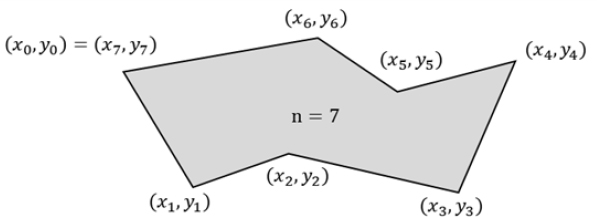
무게 중심은 xy 평면에 투영된 데이터를 다각형으로 취급하여 계산한다. Fig. 4와 같은 n개의 점을 가진 다각형의 무게 중심을 구하는 방법은 식 (1)과 같다.
| (1) |
회전 방향 정렬은 단면 이차 모멘트의 주축 정보를 이용한다. 단면 이차 모멘트의 주축은 형상을 크게 봤을 때 어느 방향으로 가장 길쭉하고 어느 방향으로 가장 짧은지를 의미하게 되므로 이의 이용은 서로 다른 형상 간의 유사한 방향을 암시하는 정보가 되기 때문이다. 원점을 기준으로 하는 n개의 점을 가진 다각형의 단면 이차 모멘트는 식 (2)와 같다.
| (2) |
이때 무게 중심을 이용하여 평행 이동하여 정렬하기 때문에 단면 이차 모멘트를 무게 중심을 기준으로 획득해야 하고, 이는 평행축 정리를 통해 구현한다. 주축 정보는 위에서 얻어진 단면 이차 모멘트를 이용해 계산한다. 이를 위해 데이터의 주축 방향 좌표계를 임의로 설정한 뒤 직교 좌표계와의 관계를 구해 식으로 표현한다.
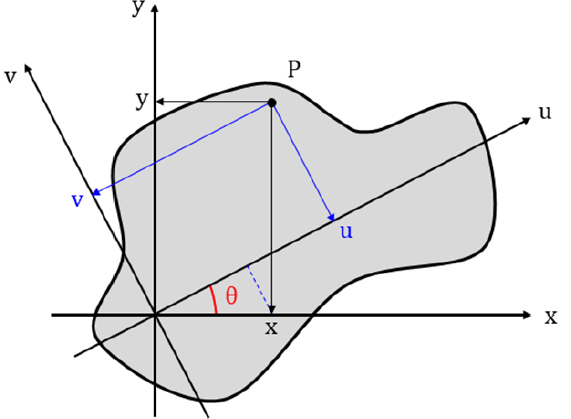
Fig. 5와 같은 단면의 직교 좌표계에서 구한 단면 이차 모멘트 식은 식 (3)과 같다[7].
| (3) |
이후 단면의 주축 방향 좌표계를 정의한다. 직교 좌표계를 기준으로 표현하면 θ만큼 회전된 좌표계이며, (u, v)라 정의한다. 이후 단면 위의 임의의 점 P(x, y)를 각각의 두 좌표계로 표현하면 두 좌표계 사이의 관계를 나타낼 수 있고, 이는 식 (4)와 같다.
| (4) |
두 좌표계 사이의 관계를 통해 단면 이차 모멘트를 주축 방향 좌표계에 대해 표현한다. 식 (5)는 변환한 단면 이차 모멘트 계산식 중 u 방향 단면 이차 모멘트 식이다.
| (5) |
같은 방법으로 단면 이차 모멘트 식을 변환하여 모든 주축 방향에 대한 단면 이차 모멘트 식인 식 (6)을 얻을 수 있다.
| (6) |
식 (6)을 보면 주축 방향 좌표계에서 단면 이차 모멘트가 직교 좌표계에서의 단면 이차 모멘트와 두 좌표계 사이의 회전각을 통해 표현할 수 있음을 볼 수 있다. 또한, 각도 θ에 대한 함수이기 때문에 θ로 미분하여 주축 방향 좌표계에서의 단면 이차 모멘트의 최댓값과 최솟값, 그리고 그때의 각도 θm을 구할 수 있다. Iuu값을 미분하여 각도 θm을 구한 최종 식은 식 (7)과 같다.
| (7) |
2.3 정합 결과 및 비교
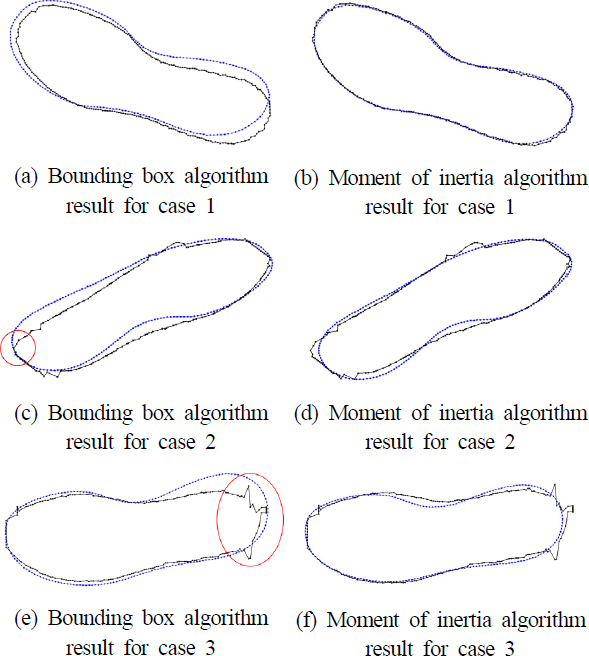
Fig. 6은 두 가지 대략적 정합 방법을 Fig. 3의 세 가지 데이터 쌍에 적용한 결과를 상단(top view)에서 바라본 이미지이다. 경계 상자를 이용한 정합 결과는, Fig. 6-(c)와 Fig. 6-(e)에 표시한 것처럼 노이즈가 포함된 경우 큰 오차를 보이는 현상이 나타난다.
정합 정확도는 오차 값을 이용하여 검증한다. 오차 값은 템플릿 데이터에 속한 각각의 점에 대해 가장 인접한 스캔 데이터에 속한 점을 구하고 점 사이의 거리를 계산하여 획득한 뒤, 모든 점에 대한 거릿값 제곱의 평균을 계산하여 얻으며, 식 (8)과 같다. 이때, P는 템플릿 데이터에 속한 점을 나타내고, 점 P′은 스캔 데이터 중 점 P와 가장 가까운 점을 나타낸다.
| (8) |
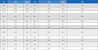
Table 1에서는 Fig. 6의 세 가지 데이터에 대해 경계 상자 방법과 이차 단면 모멘트 방법을 적용했을 때의 오차 값을 비교하였다. 표에 나타난 것과 같이 단면 이차 모멘트를 이용하여 대략적 정합을 수행하였을 때 정합 정확도가 더 높은 것을 확인할 수 있다. 이는 제안한 방법의 이차 단면 모멘트는 형상의 전반적 특징에 좌우되고 지엽적 노이즈에 의해서는 크게 변하지 않기 때문이다.
3. 3차원 곡선 데이터의 정밀한 정합
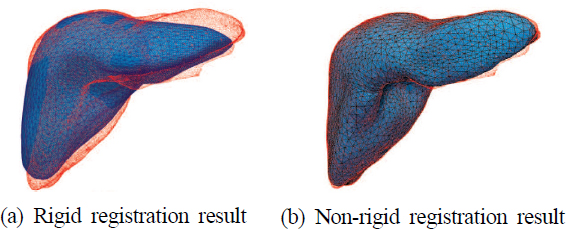
정밀한 정합(fine registration)은 대략적 정합을 통하거나, 혹은 이미 유사한 자세와 위치에 놓인 2개의 형상 데이터를 더욱 정확하게 일치시키는 과정이다. 정밀한 정합은 Fig. 7과 같이 강체 정합(rigid registration)과 비강체 정합(non-rigid registration)으로 구분한다[4]. 강체 정합은 정합을 수행할 때 평행이동과 회전이동만 적용하는 것으로, 두 데이터가 거의 유사하지 않으면 큰 오차가 발생한다. 많이 사용하는 강체 정합 방법으로는 ICP(iterative closest points) 방법이 있다[8]. 비강체 정합은 강체 정합과 달리 정합 과정에서 스트레칭(stretching)을 동반하여 데이터의 형태를 부분적으로 변형시키면서 정합 목표 데이터에 일치시키는 정합이다. 이 방법을 사용하면 두 데이터를 완전하게 일치시킬 수 있지만, 노이즈가 존재하는 경우 노이즈까지도 따라가는 문제가 발생한다. 대개의 경우 정합의 결과로 기대되는 것은, 대체로의 형상(look-see)은 추종하도록 위치되고 변형되지만, 지역적인 노이즈는 따라가지 않는 정합결과이다. 본 연구에서는 이를 위해 MBA 기법을 응용한 비강체 정합 알고리즘을 제안한다.
3.1 MBA 기법
지역적인 노이즈는 적게 추종하면서 전체적인 형상을 추종하는 스트레칭 정합을 구현하기 위해 MBA(multilevel B-spline approximation) 기법[8]을 이용한다. MBA 기법이란 목표점(target point)이 불균일하게 흩어져 있을 때 ① 이들 목표점을 지나는, ② 부드러운 곡면을 만드는 방법이다. 만들어진 결과는 z = f(x, y) 형태의 함수로 모든 (x, y) 점에 대해 z 높이를 계산할 수 있게 된다. 따라서 이는 2차원 영역에 대한 스칼라장(scalar field)이다. 이 스칼라장을 2개로 늘려서 각각에 적당한 물리적 의미를 부여하면 정의역 (x, y)에 대한 2차원 벡터장(vector field)이 된다. 한편, 정의역이 (x, y, z)가 되도록 MBA 방법을 수정할 수 있다[10]. 그러면 3차원 공간에 대한 스칼라장 v = f(x, y, z)를 얻을 수 있다. 그리고 이 스칼라장을 3개 사용하면 “3차원 공간에 대한 3차원 벡터장(vector field)”을 정의할 수 있게 된다[10]. 본 연구에서는 이와 같은 3차원 벡터장을 구성하여, 정합을 위해 각 점이 움직여야 할 변형벡터를 의미하게 하게 한다. 3차원 벡터장이 만들어질 때 MBA 기법의 특징을 이용하여, 각 스칼라장이 부드러운 변화값을 갖도록 하면 전체적인 형상을 따라가면서도 국부적인 노이즈는 자연스럽게 제거되게 할 수 있다. 일반적으로 국부적 노이즈는 심한 굴곡을 갖게 하는데, MBA 기법에 의한 보간을 적당한 반복횟수로 수행하면, 결과 스칼라장이 급격한 변화는 미처 추종하지 못하고 오차로 남겨두게 된다. 따라서 전체적 형상은 추종하지만 노이즈는 적당히 무시하는 스칼라장을 얻을 수 있게 되기 때문이다.
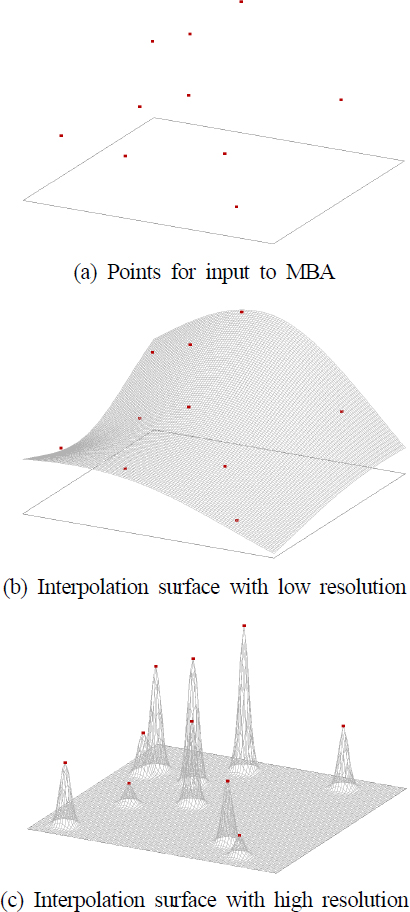
Fig. 8의 (a)에는 (x, y) 영역에 대해 불규칙하게 흩뿌려진(scattered) 점들이 주어져 있다. 이를 보간하는 곡면을 만드는 것은 2차원 정의역에 대한 스칼라장을 만드는 문제와 같다. 곡면을 만들고자 할 때 적용 방법에 따라 여러 가지의 결과가 있을 수 있다. 그림 (b)는 낮은 차수(degree)의 식으로 보간한 결과 곡면이다. 차수를 높여 해상도를 올리면 (c)와 같은 곡면이 얻어진다[9]. 그림을 보면 해상도가 낮을 때는 얻어지는 곡면이 부드럽지만 조건점을 정확히 통과하지 못하여 오차가 크게 존재한다. 반면 차수를 올리면 정확도가 증가하여 입력점을 작은 오차로 통과하지만 대신 곡면의 모양이 심한 굴곡을 가지게 된다.
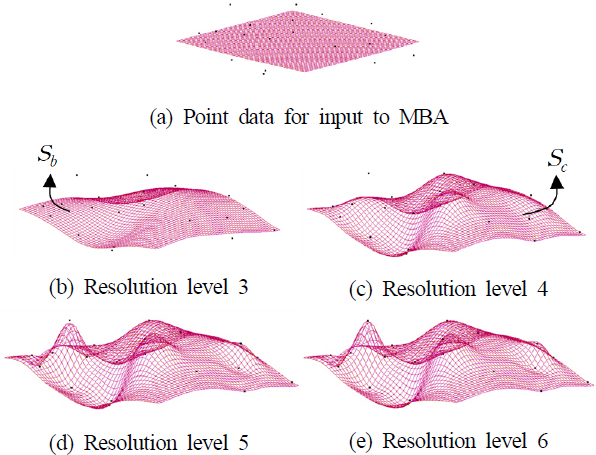
MBA 기법은 다음과 같은 순서로 진행된다. 우선 낮은 해상도로 입력점들을 보간하는 B-spline 곡면을 얻는다. 만약 해상도를 3차×3차 곡면식을 사용한다면 각 방향으로 4개 이상의 점이 있을 경우 이를 정확히 근사하는 곡선을 만들 수 없고 꽤 큰 오차를 가지는 부드러운 곡면이 된다. 본 연구에서 다루는 형상은 수백 개의 점이 곡선을 따라 존재하므로 “많은 점이 균일하게 않게 뭉쳐진 위치에 입력으로 주어지는 경우”에 해당한다. Fig. 9의 (a)의 예에는 2차원 정의역과 주어진 입력점이 있고 (b)는 이를 낮은 해상도로 보간된 곡면 Sb을 보여준다. 그림을 보면 이 곡면에는 아직 많은 오차가 존재함을 알 수 있다. 다음으로, 앞서 얻어진 (b)의 곡면 Sb를 기준으로, 남은 오차를 얻어 이를 보간해야 할 목표값으로 삼는다. 그리고 정의역을 구역별로 다시 분할한 뒤 남은 오차를 보간하기 위한 새로운 곡면 Sc-b 을 얻는다. 이를 (b)의 곡면 Sb에 더해서 곡면 Sc를 얻는다. 즉 Sc = Sb + Sc-b를 계산한다. 이렇게 하면 낮은 해상도에서 얻어졌던 부드러운 곡면에, 해상도를 높이면서 오차를 줄여가는 추가 곡면이 더해지게 되어 부드러움과 정확도가 증가된다. MBA(multi-level B-spline approximation) 기법의 명칭은 이와 같이 정의역을 다단계(multi-level)로 분할해 가면서 B-spline의 형태의 곡면으로 근사(approximation)한다는 의미를 담고 있다. 자세한 수학적 방법은 Lee[9]와 Kim[10]의 연구에 나와있다. Fig. 9의 (c), (d), (e)는 단계(level)를 더해가면서 곡면이 입력점으로 다가가는 모습을 보여준다.
한편 MBA 기법을 사용하더라도 단계(level)를 높여가면서 추가분할에 따른 오차 보정을 무한정 반복한다면 모든 입력점을 통과하는 정확한 곡면을 얻게 되어 지역적인 노이즈까지도 추종해버리게 된다. 이에 대한 대책이 필요한데 이에 대해서는 다음 절에서 설명한다.
3.2 노이즈의 영향을 최소화하기 위한 정합 전략
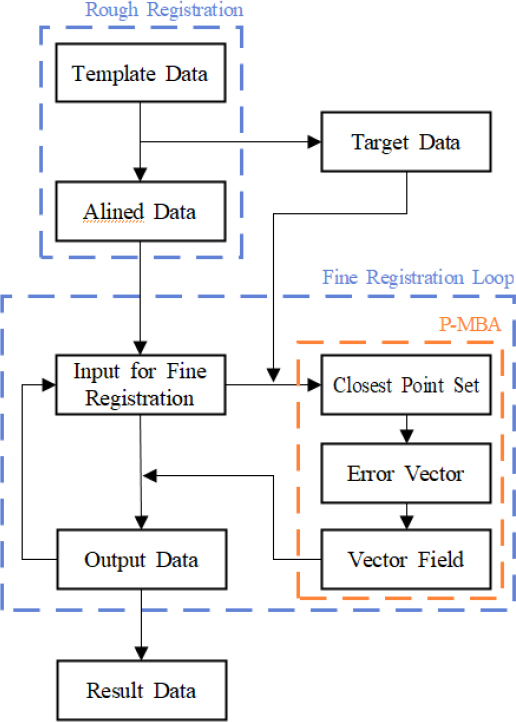
본 연구에서 지역 노이즈를 무시하게 하는 핵심 아이디어는 “노이즈를 따라가는 보간 곡면은 통상 급격한 굴곡을 가지게 되므로, 보간 곡면의 부드러움을 유지하여 형상의 경향은 추종하지만 노이즈 부분에서는 오차를 허용한다” 라는 것으로 요약된다. 따라서 추가분할에 따른 오차 보정은 적당한 선에서 중지해야 하는데, 반면 오차 보정을 충분히 하지 않으면 노이즈가 아닌 주요 형상부에서도 정확치 않은 결과를 만들어낼 수 있다. 이런 문제를 해결하기 위해 본 연구에서는 추가분할에 따른 오차 보정을 적당한 단계로만 계산하여 미완성으로 둔다. (이를 Partial-MBA, 즉 PMBA라 하겠다.) 그리고 얻어진 곡면을 초기값으로 삼아 PMBA를 다시 반복 시행하는 전략을 사용하였다. Fig. 9의 예로 보면 PMBA에서는 그림 (b)의 단계 3 혹은 그림 (c)의 단계 4정도에서 중지하여 미완성 결과를 얻고, 이를 초기값으로 다시 PMBA를 반복한다. 이때 PMBA 내부에서 정의역의 추가분할에 의한 오차 보정을 반복 계산하는 것을 내부 루프(inner loop), PMBA를 반복하는 과정을 외부 루프(outer loop)라고 부를 수 있다. 한편 PMBA를 위한 추가분할 횟수, 즉 내부 루프의 반복 횟수는 전체 형상의 굴곡도와 노이즈의 강도에 따라 달라지므로 실험에 의해 결정하였다. 또 PMBA의 반복 횟수, 즉 외부 루프의 반복 횟수도 형상과 노이즈의 양상에 따라 달라지는데 실험에 의해 결정하거나, 통계적으로 결정할 수 있다. 통계적 결정이란 오차의 평균 m과 표준편차 σ를 구해 오차가 m으로부터 +nσ를 벗어나는 데이터는 노이즈로 판단해서 무시하고 나머지 점들의 오차가 일정 범위 내로 작아지면 정지하는 방법을 말한다. 위에 설명한, 템플릿 데이터를 타겟 데이터로 정합시키는 알고리즘을 순서도로 보이면 Fig. 10과 같다.
(1) 템플릿 데이터를 타겟 데이터에 대해 대략적 정합을 수행하여 정렬된 데이터를 획득한다. 이는 정밀한 정합의 1회차 PMBA 수행을 위한 입력 데이터가 된다.
(2) 이후 타겟 데이터와 입력 데이터 사이의 인접한 대응점 쌍(closest point pair)을 찾고 오차 벡터를 구한다. 구해진 오차 벡터들은 3차원 정의역에서 각각 x, y, z방향으로 만족시켜야 할 입력값이 되는데 일반적으로 공간에 흩뿌려진 균일하지 않은 분포를 가진다. 우리가 구해야 할 것은 이 입력점 세트를 만족시키는 각각의 스칼라장이 된다. x, y, z 방향으로 3개의 입력점 세트에 대해 각각 PMBA를 반복 수행한다. 그리고 그 결과가 얻어지면 다음번 PMBA의 초기값으로 사용한다.
PMBA에서 낮은 해상도에서 정지하면 (즉 내부 루프의 반복 횟수를 작게 하면) 노이즈의 영향은 적게 할 수 있지만, 정확도가 낮아 PMBA의 반복 횟수(즉 외부 루프의 횟수)를 여러 번 수행해야 한다. 이것은 실행 시간에서 불리함을 보인다. 반면 내부 루프의 횟수를 늘리면 노이즈를 따라 가버리게 된다. 따라서 적절한 해상도를 선택이 필요하다.
한편 MBA 알고리즘은 공간을 추가분할하면서 해상도를 높여가는 방법인데 정의역이 3차원일 때 추가분할을 할 때마다 분할구간 개수의 3승의 비율로 구간의 수가 증가해서 엄청난 양의 메모리가 필요하게 된다. PMBA는 추가분할의 횟수를 제한하므로 메모리를 합리적으로 사용하는 효과도 있다. 본 연구의 예에서는 PMBA를 위한 내부 루프 반복을 2회 혹은 3회로 하였다.
(3) PMBA를 반복하다가 정합이 완료되었다고 판단되면 반복을 중단한다. 이렇게 x, y, z에 대한 각각의 스칼라장이 얻어지면 이들 3개를 모아 3차원 공간에 대한 3차원 벡터장을 만들 수 있다. 그리고 이것이 곧 정합을 위해 템플릿 데이터를 변화시키기 위한 각 점의 이동량이 된다.
3.3 정합 결과
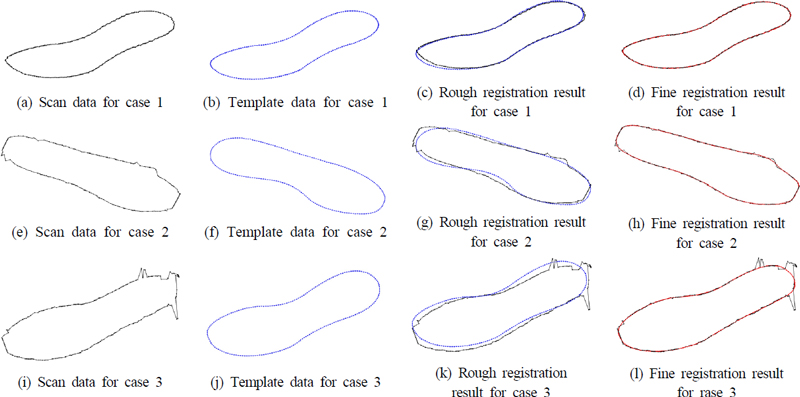
본 논문에서 제안한 방법을 통해 대략적 정합 이후 정밀한 정합을 수행한 결과는 Fig. 11과 같다. 세 가지 사례에 대해 타겟 데이터, 템플릿 데이터, 대략적 정합의 결과, 정밀 정합의 결과를 보여준다. 정밀 정합의 결과를 보면 세 경우 모두, 전체적인 형상은 추종하되 노이즈는 따라가지 않는 것을 확인할 수 있다. 두 번째 사례의 경우는 곡선 전체에 걸쳐 비교적 작은 노이즈들이 존재하는데 정합에서 이들이 무시된 것을 볼 수 있다. 또 세 번째 사례에서는 앞굽 쪽에 작은 노이즈와 뒤꿈치 쪽에 비교적 큰 노이즈가 존재하는데, 역시 이를 무시하는 정합결과가 얻어짐을 볼 수 있다.
제안한 알고리즘으로 정합을 수행한 후 발생한 오차와 정합에 소요된 시간이 Table 2에 보여져 있다. 이를 보면 두 번째와 세 번째 사례에서 오차가 더 크게 나타난다. 이는 노이즈를 따라가지 않고 정합되었기 때문에, 노이즈가 없는 첫 번째 사례에 비해 큰 오차가 발생한 것으로 이해할 수 있다. 한편 정합을 위해 최대 0.6초 정도의 시간이 소요되어 생산 자동화를 위해서 수용 가능한 정도로 판단된다.
4. 결 론
본 논문에서는 3차원 곡선 데이터에 대해 대략의 형상은 추종하면서 부분 불량형상은 무시하는 스트레칭 정합 방법을 제안하였다. 이 방법에서는 MBA 방법을 낮은 해상도로 적용하여(PMBA 방법) 급격한 굴곡은 따라가지 못하도록 하되, 주요 형상은 추종하도록 PMBA를 반복하여 시행한다. 제안한 정합 알고리즘을 세 가지 사례의 3차원 곡선 데이터에 적용해 보았다. 세 가지 사례는 노이즈가 없는 경우, 작은 노이즈가 있는 경우, 큰 노이즈가 있는 경우이다. 세 가지 사례 모두 주요 형상에는 일치되고 노이즈는 거의 무시하면서 정합되는 것을 확인하였다. 또 수백 개의 점 데이터에 대해 0.6초 이내의 실행 시간을 보여 실시간 자동화를 위해 적용 가능함을 보여주었다.
한편 대략 정합을 위해 2차원 도형 사이에 단면 모멘트에 의한 주축 정렬 방법을 제안하였다. 이는 도형의 면 특성(area property)을 이용하는 것으로 지역적인 노이즈에 크게 좌우되지 않는 성능을 보임으로써 정밀정합을 위한 좋은 초기조건을 제공함을 확인할 수 있었다.
제안된 정합 방법은 중창의 자동 스프레이 장비에 적용되어 성공적으로 사용되고 있다. 특히 노이즈가 비교적 많이 발생하는 저가 스캐너의 채용을 가능하게 하여 비용 경쟁력 있는 장비 개발에 큰 기여를 하였다.
References
-
Besl, P. J., McKay, N. D., 1992, A Method for Registration of 3-D Shapes, IEEE Transactions on Pattern Analysis and Machine Intelligence, 14:2 239-256.
[https://doi.org/10.1109/34.121791]

-
Zhang, Z., 1994, Iterative Point Matching for Registration of Free-Form Curves and Surfaces, Int. J. Comput. Vis., 13 119-152.
[https://doi.org/10.1007/BF01427149]

-
Chen, Y., Medioni, G., 1991, Object Modeling by Registration of Multiple Range Images, IEEE International Conference on Robotics and Automation, 4102093.
[https://doi.org/10.1109/ROBOT.1991.132043]

-
Kang, N., Lee, M. W., Rhee, T., 2012, Simulating Liver Deformation during Respiration Using Sparse Local Features, IEEE Computer Graphics and Applications, 32:5 29-38.
[https://doi.org/10.1109/MCG.2012.65]

-
Allen, B., Curless, B., Popović, Z., 2003, The Space of Human Body Shapes: Reconstruction and Parameterization from Range Scans, ACM Trans. Graph., 22:3 587-594.
[https://doi.org/10.1145/882262.882311]

-
Zhang, Z., Prinet, V., 2002, A Rough-to-Fine Satellite Image Registration Method with Sub-Pixel Accuracy, IEEE International Conference on Image Processing, 7603794.
[https://doi.org/10.1109/ICIP.2002.1038986]

- Beer, F., Johnston, E., DeWolf, J., Mazurek, D., 2015, Mechanics of Materials, McGraw-Hill, NewYork.
-
Rusinkiewicz, S., Levoy, M., 2001, Efficient Variants of the ICP Algorithm, Proceedings Third International Conference on 3-D Digital Imaging and Modeling, 145-152.
[https://doi.org/10.1109/IM.2001.924423]

-
Lee, S., Wolberg, G., Shin, S. Y., 1997, Scattered Data Interpolation with Multilevel B-Splines, IEEE Transactions on Visualization and Computer Graphics, 3:3 228-244.
[https://doi.org/10.1109/2945.620490]

- Kim, S. H., Song S. J., 2007, A Method for Modifying a Surface Model with Nonuniform Scattered Constraint Points, Korean Journal of Computational Design and Engineering, 12:1 58-73.

Graduate Student in the Department of Mechanical Design and Robot Engineering, Seoul National University of Science and Technology.
His research interest is Machine Vision and Automation System.
E-mail: 0013025@seoultech.ac.kr

Master of Science in the Department of Mechanical Design and Robot Engineering, Seoul National University of Science and Technology.
Her research interest is Machine Vision and Deep Learning.
E-mail: lyn2344@seoultech.ac.kr

Professor in the Department of Mechanical System Design Engineering, Seoul National University of Science and Technology.
His research interest is Manufacturing System and Machine Vision.
E-mail: sunghwan@seoultech.ac.kr