롤러-랙 피니언 시스템의 이뿌리 굽힘응력
Abstract
A tooth root bending stress equation for a roller-rack and pinion (RRP) system is presented in this paper as a solution to the problem of tooth root breakage in a pinion jacking system based on an involute tooth profile. The bending strength geometry factor for the RRP system was determined by the same procedure as that for the involute tooth profile. The tooth root bending stress of the RRP system was found to be lower than that of the involute teeth with the same design specification. It can also be lowered by increasing the profile shift coefficient and the number of teeth of the pinion, and by decreasing the roller diameter coefficient. Finally, it was confirmed that the RRP system could provide a new solution to the bending strength problem of a conventional rack and pinion system.
Keywords:
RRP(roller-rack and pinion), Tooth root bending stress, Tooth form factor, Fatigue stress concentration factor, Bending strength geometry factor1. 서 론
잭업 장치용 랙-피니언(rack-pinion) 파손은 대부분 절손 형태로 일어나며, 주로 이뿌리 부에 발생하는 인장 굽힘응력에 기인한다. 이러한 기어 이뿌리 부 파손문제는 기어 연구자들의 주된 관심사이며 현재도 다양한 굽힘강도 연구들[1]이 수행되고 있다.
본 논문에서도 잭킹(jacking) 피니언 절손으로 인한 파손 문제 해결의 일환으로 다 접촉, 구름 접촉으로 인해 내마멸 특성이 탁월한 RRP (roller-rack and pinion) 시스템[2,3]을 고려하였고, 이의 굽힘응력을 평가하고자 한다. 하지만 RRP 시스템에 대한 굽힘강도 해석은 치형계수(tooth form factor) 및 피로응력집중계수(fatigue stress concentration factor) 등의 결정이 지난하여 아직 보고된 바 없다. 이에 본 논문에서는 Lewis 굽힘응력 식에 기반한 인벌류트 치형의 치형계수 산정과 동일한 절차로 굽힘하중과 위험단면을 찾아 RRP 시스템 이뿌리 부 굽힘응력을 결정하고자 한다. 또한 ISO 6336, AGMA 2001-D04 규격을 이용한 인벌류트 치형의 굽힘응력과 RRP 시스템의 굽힘응력 비교평가를 통하여 기존 인벌류트 치형 기반 랙-피니언의 치 절손 문제에 대한 RRP 시스템의 대안 가능성을 확인하고자 한다.
2. 접촉력 및 물림률
2.1 접촉력
최근 Nowoisky[4]는 보트 리프트용 잭킹 피니언의 굽힘응력에 대하여 고찰한 바 있으며, 이의 설계제원과 RRP 시스템의 설계제원을 Table 1에 나타내었다. 이때 동일 잇수, 동일 모듈(module), 동일 전위계수(profile shift coefficient), 동일 이 폭(face width)을 고려하였다.
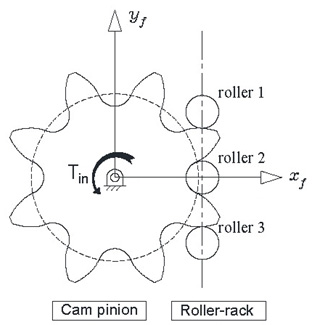
Table 1의 형상설계제원을 기반으로 설계된 RRP 시스템의 초기 접촉형상은 Fig. 1과 같다. 이때, 피니언이 반시계 방향 회전 시 물림 이탈이 빠른 시간 순서로 롤러들의 접촉번호를 지정하였다.
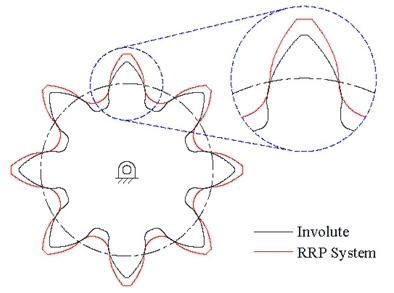
Fig. 2는 인벌류트 치형과 RRP 시스템 치형을 대비한 그림이며, RRP 시스템의 치형은 인벌류트 치형보다 디덴덤(dedendum)은 감소하고 어덴덤(addendum)은 증가한 형태를 보였고, 대부분 높이 구간에 걸쳐 이두께(tooth thickness) 또한 커지는 경향을 보였다. 따라서 강도설계 시 두 치형은 상당한 차이를 가지리라 예측된다.
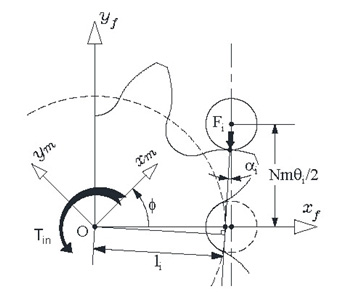
Fig. 3과 같이 피니언이 입력 토크 Tin에 의해 초기 위치로부터 ϕ만큼 회전을 했을 때, Nmθi/2 의 위치에 놓인 i-번째 롤러에서의 접촉력 Fi는 일정 접촉강성(equal mesh stiffness) 가정 하에 다음과 같이 결정[5]할 수 있다.
| (1) |
여기서 li는 모멘트 팔, n은 피니언과 롤러 사이의 초기 접촉개소 그리고 θi는 i-번째 롤러의 위치각을 의미하고 각각은 다음과 같다.
| (2) |
| (3) |
| (4) |
이때 N은 피니언의 잇수, m은 모듈, αi는 압력각, β는 피니언의 이 높이를 결정하는 치선연장계수(addendum extension factor), [ ]는 내림함수(floor function), ϕ는 접촉이 유지되고 힘이 작용하는 구간까지의 피니언의 회전각(roll angle) 그리고 θp는 피치 회전각을 의미한다.
2.2 물림률
물림률(contact ratio, ϵ)은 어떤 한 순간에 접촉 상태에 있는 평균 잇수로 정의하며 일반적인 인벌류트 기어의 경우 압력각이 일정하므로 물림길이 결정을 통해 이를 쉽게 결정할 수 있으나, 가변 압력각을 갖는 RRP 시스템의 경우 치선연장계수 β의 함수로서 1 ≤ β < 2인 경우 다음과 같이 물림률을 결정[6]할 수 있다.
| (5) |
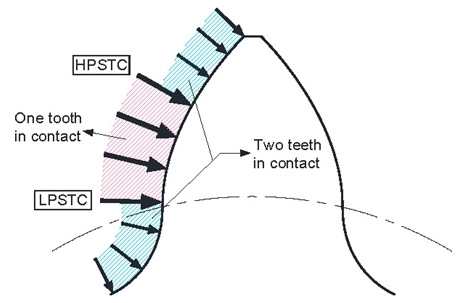
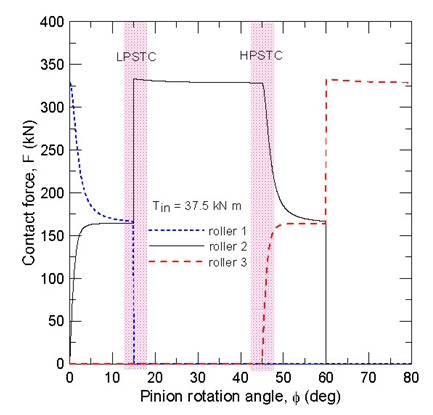
Table 1의 설계 제원에 따르면 RRP 시스템은 1.5의 물림률을 가지므로 동일 설계제원의 인벌류트 랙-피니언 물림률 1.117 보다 큰 물림률을 가짐을 알 수 있다. 이는 기어 이들이 맞물려 회전할 때 인벌류트 치형은 11.7% 물림구간에서 두 쌍의 이가 하중을 분담(sharing)하며 88.3% 물림구간에서 한 쌍의 이가 하중을 전담함에 비해, RRP 시스템의 경우 50% 구간에서 두 쌍의 이가 기어 전달하중을 분담하며, 나머지 50% 구간에서 한 쌍의 이가 하중을 전담함을 의미한다. Fig. 4는 RRP 시스템의 피니언 치 하나의 전 높이에 대해 물림률을 설명한 그림이다.
Fig. 5는 RRP 시스템의 접촉력 변화를 도시한 그림이다. 롤러 2가 유효접촉을 시작(Fig. 1 참조)하는 구간부터 하중전담시작지점 LPSTC (lowest point of single tooth contact)까지는 롤러 1, 롤러 2와 유효접촉을 하는 두 쌍의 치가 하중을 분담하고, 롤러 1이 접촉을 이탈한 후부터 하중전담종료지점 HPSTC (highest point of single tooth contact)까지는 롤러 2와 접촉하는 한 쌍의 치만이 하중을 전담한다. 그리고 다시 HPSTC 이후 부터 롤러 2가 접촉이탈을 하기 전까지 롤러 2, 롤러 3과 유효 접촉을 하는 두 쌍의 치가 하중을 분담한다. 이러한 하중의 주기적 변화는 기어 이 표면 피팅(pitting) 및 이뿌리 부 절손의 주요 원인으로 알려져 있다. 일반적으로 기어 이의 피팅은 LPSTC 부근에서 지배적이며, 기어 이 절손은 단일접촉 최고위치인 HPSTC에서의 굽힘하중으로 인한 이뿌리 굽힘응력에 기인한다.
3. 이뿌리 굽힘응력
일반적인 기어와 마찬가지로 RRP 시스템 또한 Figs. 4, 5와 같이 치 한 쌍이 모든 하중을 전담하는 최악하중점인 HPSTC에서의 굽힘응력 식을 기반으로 굽힘 강도설계를 수행하여야 한다.
즉 기어 이에 내접하는 균일 강도 포물선 보(Fig. 6 참조)로부터 치형계수를 결정하여 다음과 같이 이뿌리 부 굽힘응력(tooth root bending stress)을 결정 할 수 있다.
| (6) |
여기서 nd는 Ko, Kv, Ks, Km, KB 등의 AGMA 또는 ISO 보정계수들을 고려한 전 보정계수(full correction factor), Ft는 단일접촉 최고위치인 HPSTC에서의 접선력(transmitted tangential load)이며, b는 피니언의 이 폭, 그리고 Yj는 굽힘강도 형상계수(bending strength geometry factor)로 Y / Kf의 값을 갖는다. 이때 Y는 모듈기반 치형계수, Kf는 이뿌리 부 피로응력집중계수를 나타낸다.
3.1 굽힘하중
RRP 시스템 피니언의 단일접촉 최고위치인 HPSTC에서의 접선력 또는 굽힘하중 Ft는 다음과 같이 결정할 수 있다.
| (7) |
여기서 F는 HPSTC에서의 접촉력이며, 하중각(load angle) γ는 다음과 같다.
| (8) |
이때 e는 전위계수를 의미한다.
3.2 치형계수
인벌류트 치형의 치형계수는 잇수와 압력각의 함수인 반면, RRP 시스템의 치형계수는 잇수(N), 전위계수(e), 롤러직경계수(roller diameter coefficient, Cr)의 함수이다. 최근 Kwon과 Cha[7]는 작도법에 의해 RRP 시스템의 치형계수 결정방법을 소개한 바 있으나, 본 논문에서는 이론적으로 치형계수를 결정하고자 한다.
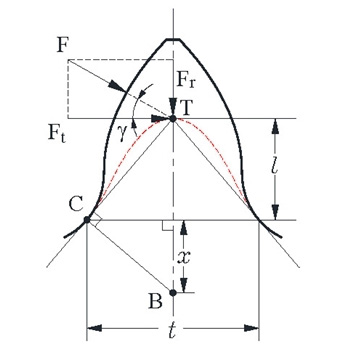
Fig. 6과 같이 기어 이에 내접하는 균일강도 포물선 꼭지점(T) 좌표(xt, yt)는 최악하중점인 HPSTC에서의 작용선(line of action)과 치 중심선과의 교점의 좌표로서 다음과 같이 결정할 수 있다.
| (9) |
위험단면 좌표점(C)은 RRP 치형을 롤러 또는 핀 반지름만큼 확대 오프셋한 치형의 임의의 좌표를 미분한 결과와 포물선 꼭지점(T)과 오프셋 치형의 임의 좌표에 대응되는 임의의 치 형상 점을 잇는 직선의 기울기를 비교하여 오차가 가장 작은 임의의 치 형상 점을 위험단면 좌표로 지정하였다.
그리고 포물선 꼭지점(T)과 위험단면 좌표(C)를 잇는 직선상에서 내린 수선과 치 중심선이 만나는 점을 굽힘응력 결정 좌표(B)로 결정하였다. 이를 통하여 다음과 같이 치형계수(Y)를 결정하였다.
| (10) |
본 논문의 Table 1의 설계제원에 따른 치형계수(Y)는 0.6345로 평가되었다.
4. 결과 검토
이론을 통하여 구하지 못한 피로응력집중계수를 결정하기 위하여 다음의 일반적인 피로응력집중계수 결정 식을 고려하였다.
| (11) |
여기서 q는 노치민감도계수(notch sensitivity factor)이며, 본 논문에서는 보수적 설계를 위하여 1로 가정하였다. 그리고 Kt는 응력집중계수이며 다음 식을 통하여 결정할 수 있다.
| (12) |
여기서 (σ)FE는 FE해석을 통해 결정한 von-Mises 등가응력을 나타내며, (σ)Theory는 식 (6)의 굽힘응력(σb)과 반경하중(Fr, Fig. 6 참조)으로 인한 압축응력(σn), 접선력(Ft)에 기인한 전단응력(τr)을 모두 고려한 이론적 von-Mises 등가응력을 나타낸다.
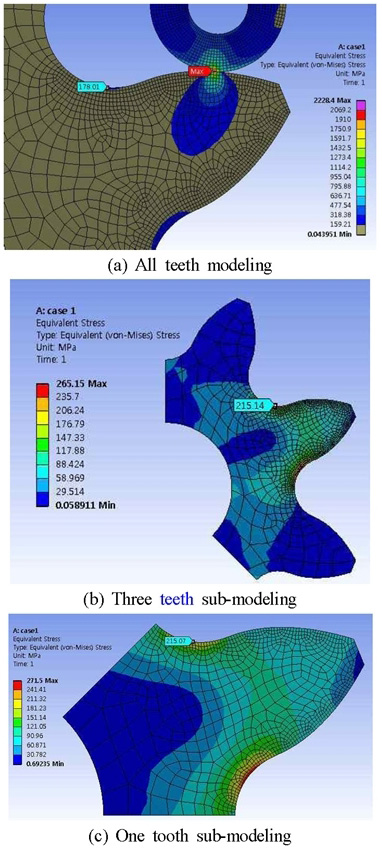
식 (12)에 의한 응력집중계수 평가를 위해 전체 치형, 치 3개, 그리고 치 1개를 고려하여 FE 굽힘응력 해석을 수행하였으며 각 모델링별 차이가 발생하는 지 검토하였다.
Fig. 7(a)는 피니언 전체 치(롤러-랙 포함)를 모델링하였으며, “hexahedral mesh”를 적용하여 3D 해석을 수행하였다. 이때 피니언의 크기, 해석의 정확도를 고려하여 피니언과 롤러가 접하는 부분과 이뿌리 부는 “edge mesh” 기능을 사용하여 1.0 mm의 조밀한 메쉬를 적용하였다. 또한 피니언과 롤러의 접촉은 마찰계수 0.1의 “frictional” 접촉 조건을 고려하였고, Tin= 37.5 (kN·m)를 가하여 해석한 결과이다. Figs. 7(b) 및 7(c)는 치 3개 및 치 1개만을 모델링하였고, “quadrilateral mesh”를 적용하여 2D 해석을 진행하였다. 또한 Fig. 7(a)의 해석조건과 마찬가지로 접촉력을 받는 부분과 이뿌리 부는 “edge mesh” 기능을 사용하여 1.0 mm의 메쉬를 적용하였으며, HPSTC 위치에 접촉력 F=328.64 (kN)의 집중하중을 부과하여 해석한 결과들이다.
Table 2에서 볼 수 있듯이 치 3개 및 치 1개를 모델링하여 해석한 결과는 차이가 거의 없었으나, RRP 시스템의 전체를 모델링한 결과와는 큰 차이를 보이고 있다. 이는 접촉점에 집중하중을 가하는 것과 토크를 인가하여 해석한 차이에 기인한다. 본 논문에서는 노치민감도계수 선정과 마찬가지로 보수적 설계를 위해 집중하중을 인가하여 해석한 결과에 기반하여 이뿌리 부 굽힘응력을 산정하였다.
즉 Nowoisky[4]가 ISO 6336과 AGMA 2001-D04 규격을 통하여 산출한 굽힘응력과 RRP 시스템에서의 굽힘응력을 Table 3에 비교 제시하였으며, 동일 설계제원을 갖는 RRP 시스템의 이뿌리 굽힘응력이 인벌류트 치형보다 낮은 값을 가지는 것을 확인 할 수 있다.
4.1 전위계수의 영향
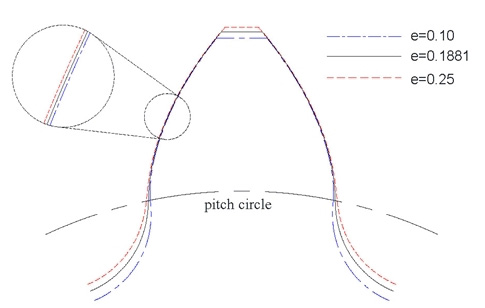
본 절에서는 RRP 시스템에서 전위계수가 치형계수 또는 굽힘응력에 어떠한 영향을 미치는 지 검토하기 위해 Table 1의 설계제원(e=0.1881) 보다 작은 전위계수 값과 큰 값의 전위계수 값을 함께 고려하였다.
Fig. 8은 전위계수에 따른 피니언의 치형 변화를 도시한 그림이다. 전위계수의 증가에 따라 디덴덤은 감소, 어덴덤은 증가하였으며, 치 높이 전체에 걸쳐서 이두께 또한 증가하였다. 이를 통하여 전위치형이 이뿌리 부 굽힘강도 보강에 긍정적 효과를 주리라 예측할 수 있으며, Table 4에서 구체적 수치로 이를 확인할 수 있다. 즉 전위계수가 증가하면 치형계수는 증가하며 피로응력집중계수는 변화 없이 거의 일정하기에 식 (6)의 형상계수 Yj(=Y / Kf)가 증가하여 이뿌리 부 굽힘응력이 작아짐을 알 수 있었다. 참고로 Table 4의 피로응력집중계수 Kf는 이 하나만을 모델링한 후 HPSTC에 접촉력을 가하여 유한요소 해석한 결과를 통해 결정한 값이다.
4.2 롤러직경계수의 영향
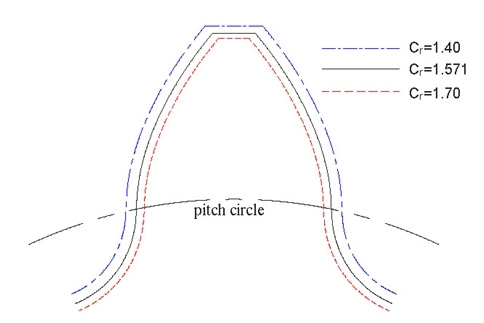
롤러직경계수(Cr)가 굽힘강도 형상계수 또는 이뿌리 굽힘응력에 미치는 영향을 검토하고자 롤러직경계수에 따른 치형 변화를 Fig. 9에 도시하였다.
롤러직경계수의 변화는 등거리 오프셋(equidistant offset) 치형의 결과로 귀결됨을 알 수 있다. 따라서 롤러직경계수가 감소하면 치형이 확대되어 치형계수 및 피로응력집중계수 모두 증가하나, 치형계수의 증가폭이 더 커 식 (6)의 형상계수 Yj가 증가함으로 인해 이뿌리 부 굽힘응력이 작아짐을 Table 5에서 확인할 수 있다.
4.3 잇수의 영향
마지막으로 RRP 시스템의 잇수(N)가 이뿌리 부 굽힘응력에 미치는 영향을 검토하였다.
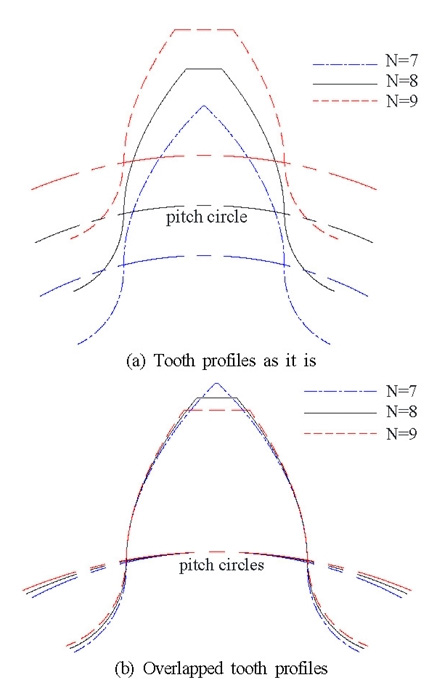
Fig. 10은 피니언의 잇수에 따른 치형의 변화를 도시한 그림이며, Fig. 10(a)와 같이 잇수가 커지면 기어 피치원(pitch circle) 또한 커져 치형들의 직접적인 비교가 어려워지기에 Fig. 10(b)와 같이 각 피치원의 정점들을 일치시켜 치형들을 비교하였다. 잇수가 증가함에 따라 디덴덤, 어덴덤, 그리고 치 높이 모두 감소하였으나, 이두께는 증가하였다.
결론적으로 잇수가 증가하면 치형계수와 피로응력집중계수 모두가 증가하나 식 (6)의 형상계수 Yj 또한 증가하기에 이뿌리부 굽힘응력이 작아짐을 Table 6에서 확인할 수 있다.
5. 결 론
본 논문에서는 랙-피니언 기반 잭킹 피니언의 치 절손 문제를 해결하기 위해 랙 치형을 직선이 아닌 원형 치형으로 대체한 RRP 시스템에서의 이뿌리 굽힘응력을 평가하고자 하였고, 그 결과를 요약하면 다음과 같다.
Lewis 굽힘응력 식에 기반한 인벌류트 치형의 치형계수 산정과 동일한 절차로 HPSTC에서 굽힘하중과 위험단면을 찾아 RRP 시스템에 대한 치형계수를 결정하였다. 또 이뿌리 부에서의 피로응력집중계수는 FE해석을 통해 결정하였다. 이를 통하여 결정되어진 RRP 시스템의 굽힘응력은 동일 설계제원의 인벌류트 치형보다 낮은 굽힘응력 값을 가짐을 알 수 있었다.
또한 RRP 시스템의 이뿌리 굽힘응력은 설계제원들 중 전위계수와 피니언의 잇수가 증가할수록, 롤러직경계수는 감소할수록 작아짐을 확인하였다. 하지만 피니언 잇수의 증가는 피니언 이 전체 크기의 증대, 롤러직경계수의 감소는 랙 강도저하를 수반하므로 신중한 선택이 요구된다.
최종적으로 기존 인벌류트 치형 기반 랙-피니언의 치 절손 문제에 대한 대책으로 RRP 시스템이 새로운 대안이 될 수 있음을 확인하였다.
Acknowledgments
본 연구는 2017년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다. (No. 20173030024690)
References
-
Aziz, I. A., Idris, D. D., Ghazali, W. M., (2017), Investigating Bending Strength of Spur Gear: A Review, MATEC Web of Conferences, 90(01037), p1-10.
[https://doi.org/10.1051/matecconf/20179001037]

-
Kwon, S. -M., (2017), Contact Fatigue Life of Rack-Pinion for Small-Sized Sluice Gate, Journal of the KSMTE, 26(3), p299-305.
[https://doi.org/10.7735/ksmte.2017.26.3.299]

-
Kwon, S. -M., (2017), Contact Fatigue Life of a Jacking Pinion for Jack-up Rig, Trans. Korean Soc. Mech. Eng. A, 41(12), p1187-1193.
[https://doi.org/10.3795/ksme-a.2017.41.12.1187]

- Nowoisky, A., (2018), Predicting Life on Through Hardened Steel Rack and Pinion for Jacking Application in the Offshore Industry, GEAR TECHNOLOGY, The Journal of Gear Manufacturing, 35(4), p36-42.
- Kim, C. H., (2014), A Study on Rack-pinion System Using Roller Gear Mechanism, A Thesis for a Doctorate, Changwon National University, Republic of Korea.
- Nam, H. C., (2013), A Study on Tooth Profile Design for Rotary Motion Gear System Based on Roller Gear Mechanism, A Thesis for a Doctorate, Changwon National University, Republic of Korea.
- Kwon, S. -M., Cha, D. I., (2018), Tooth Form Factor Determination of RRP System by a Graphical Layout, KSMTE Annual Spring Conference, p203.