단차에 대한 촉각 인지 역치 측정

1. 서 론

1.2 관련 연구

단차에 대한 역치 측정과 관련된 연구는 하나 또는 반복된 미세 돌기를 인지하기 위한 최소 높이(절대 역치, absolute threshold)를 구하기 위한 연구와 서로 다른 단차의 차이를 인지하기 위한 최소 높이 차(상대 역치, differential threshold)를 구하기 위한 연구로 나눌 수 있다.

먼저 절대 역치 측정과 관련된 연구로는 Johansson & LaMotte의 매끈한 평면에 만들어진 단일 미세 돌기를 대상으로 한 연구가 있다^[1]. Johansson & LaMotte는 포토(photo lithography) 리소그래피와 식각(etching) 공정을 이용하여 실리콘 웨이퍼 상에 원뿔대 형상의 단일 돌기를 지름과 높이를 변화시키면서 제작하였고, 이를 이용하여 미세 돌기 인지를 위한 절대 역치를 측정하였다. 그 결과, 인지를 위한 최소 높이는 미세 돌기의 반지름이 증가할수록 작아져 지름이 500 μm 이상으로 커지면 그 값이 1 μm 정도가 된다고 보고하였다. 하지만 이러한 일련의 실험은 상대적으로 적은 수의 시편(동일한 지름에 대해 4가지 높이)이 사용되어 정확도 측면에서 신뢰성이 부족하다고 할 수 있다. 또한, 원뿔대가 45°의 경사를 가지도록 제작되어 90°의 경사를 지닌 단차에 대해서는 그 값이 어떻게 달라지는지 확실치 않으며, 손가락 움직임 방향에 대한 고려가 없어 이에 대한 영향을 알 수 없다는 한계가 있다.

한편, LaMotte & Whitehouse는 유리에 만들어진 미세 돌기(20° 경사를 갖는 원뿔대)를 이용하여 Johansson & LaMotte가 수행한 것과 유사한 연구를 수행하였다[2]. 하지만 이 연구에서는 앞선 연구와 달리 손가락을 자유롭게 움직이는 능동적 방식의 실험이 아니라 손가락은 고정된 채 시편이 움직이는 수동적 방식의 실험이 사용되었다. 그 결과 인지 방식(능동적, 수동적)이 미세 돌기를 인지하기 시작하는 최소 높이에 큰 영향을 주지 않음을 알 수 있었다. 또한, LaMotte & Srinivasan은 유리에 경사각이 20°인 원뿔대 또는 평행 막대가 반복적으로 배치된 시편을 만들어 절대 역치를 측정하였다^[3]. 그 결과 피실험자가 인지하기 시작하는 미세 형상의 높이는 원뿔대보다 사각뿔대가 더 작음을 알 수 있었다.

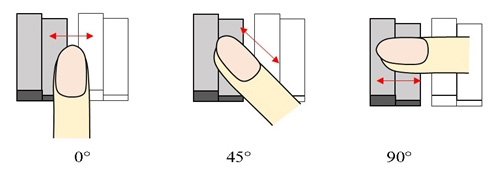
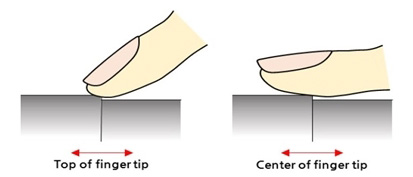
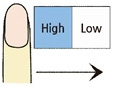
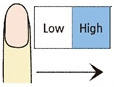
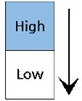
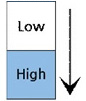
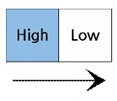
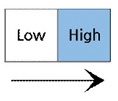
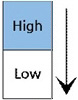
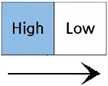
상대 역치 측정과 관련해선 Kawamura, Ohka, Miyaoka & Mitsuya가 90° 경사각을 갖는 미세 단차를 구현할 수 있는 시스템을 압전소자(Piezo electric acuator)를 이용하여 개발하고 PEST (Parameter Estimation by Sequential Testing) 방법을 이용하여 상대 역치를 측정하였다^[4]. 그 결과, 5-15 μm 범위에 있는 기준 단차에 대해 그 차이를 인지할 수 있는 최소 수준의 차이값은 2-3 μm임이 보고되었다. 더불어 이 값은 손가락과 시편의 접촉 방식이 수동적이냐 능동적이냐에 관계없이 유사한 값을 지닌다고 보고되었다. 하지만 Kawamura, Otobe & Tani에 의한 후속 연구^[5]에서는 기준 단차가 50 μm 이상인 경우에는 접촉 방식이 능동적일 때가 수동적일 때보다 상대 역치가 작다고 보고되었다. 이 외에도 미세 단차에 대한 상대 역치에 영향을 줄 수 있는 인자들에 대한 연구가 이루어졌다. 그 예로서 Ohka, Kawamura, Miyaoka & Mitsuya는 시편 움직임 속도를 달리하여 단차에 대한 상대 역치를 측정함으로써 시편 속도가 증가할수록 상대 역치는 커진다는 사실을 밝혀냈다^[6]. 또한, Kawamura, Tanaka & Tani는 Fig. 1. 과 같이 자극이 움직이는 방향이 단차를 인지하는 인간의 촉감에 어떻게 영향을 미치는지 상대 역치 측정을 통해 알아보았다^[7]. 그 결과, 기준 시편과 비교 시편이 동일한 방향으로 주어졌을 경우에는 방향에 따른 상대 역치의 차이가 없음이 보고되었다. 하지만 기준 시편과 비교 시편이 다른 방향으로 주어졌을 경우(예: 0° vs. 45°, 0° vs. 90°)에는 동일한 방향으로 주어졌을 때(예: 0° vs. 0°)와 비교하여 유의미한 차이가 있음이 보고되었다. 한편, Kawamura, Tani & Yamada는 Fig. 2와 같이 시편과의 접촉 부위가 달라짐에 따라 상대 역치가 어떻게 달라지는지 비교해 보았는데^[8], 손가락 끝의 중심부에서 접촉이 이루어질 때가 상부에서 이루어질 때보다 상대 역치가 작아짐을 알 수 있었다.

Fig. 1

Presentation angle of the step (redrawn from [8])

Fig. 2

Fingertip region in contact with the step (redrawn from [8])

앞선 연구와 관련하여 본 연구는 다음과 같은 사항들에 주안점을 두고 수행될 예정이다. 첫째, 본 연구에서는 Johansson & LaMotte의 연구^[1]에서와 같이 포토 리소그래피와 식각 공정을 이용하여 미세 단차를 가진 시편을 만들고 정신물리학 실험을 통해 절대 역치를 측정한다. 단, Johansson & LaMotte가 사용한 미세 돌기는 실리콘 웨이퍼에 제작된 경우 45°, 유리판에 제작된 경우 20°의 경사각을 지니나 본 연구에 사용되는 미세 단차는 90°의 경사각을 지니도록 제작된다. 또한 본 연구에서 사용되는 시편의 경우 수 나노미터 단위의 단차 제어 및 충분한 수의 시편 확보가 가능하여 앞선 연구(0.3-1.8 μm 범위에서 4개의 시편 사용)에 비해 보다 정확한 측정이 가능하다고 판단된다. 더불어, 본 연구에서는 20명 이상의 피실험자를 확보하여 앞선 연구에 비해 통계적으로 보다 신뢰할 만한 측정이 가능하다고 판단된다.

둘째, 본 연구에서는 Kawamura, Tanaka & Tani의 연구 방법^[7]을 받아들여 손가락 움직임 방향이 인지에 미치는 영향을 살펴보는데 주안점을 둔다. 단, 본 연구에서는 단차에 대한 상대 역치 측정이 아닌 절대 역치 측정을 통해 이를 수행할 예정인데, 손가락 움직임 방향은 45° 방향을 제외한 민감도가 가장 높은 0°와 가장 낮은 90°만을 고려할 예정이다. 더불어 그 결과에 대한 논의 역시 신경생리학적(neurophysiology) 관점에 주안점을 둔 앞선 연구와 달리, 제품의 불량 판정 기준 및 디자인적 활용 방안을 위한 토대를 세우는데 집중될 예정이다.

2. 시편 제작 및 측정

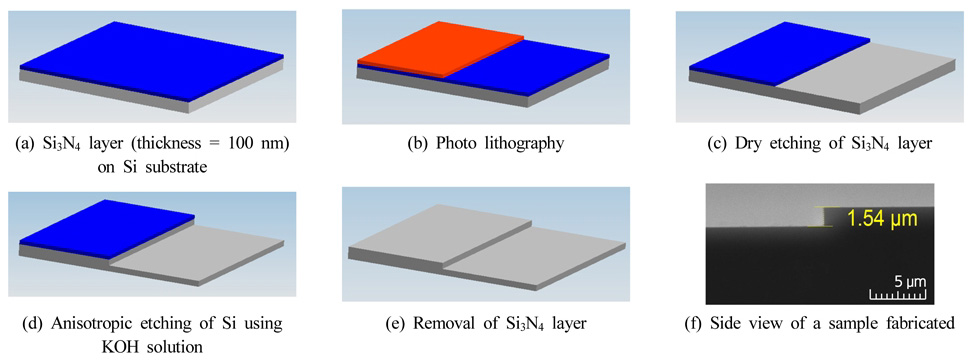
실험에 사용될 시편은 앞서 언급했듯 포토 리소그래피와 식각 공정을 사용하여 10 nm 이하의 정밀도로 Fig. 3과 같은 과정을 거쳐 제작되었다. 그 과정을 설명하면 다음과 같다. 먼저 4인치 <100> 실리콘 웨이퍼에 Si₃N₄(실리콘 나이트라이드) 층을 증착한다(Fig. 3a). 다음으로는 감광제(photoresist)를 spin coating하고 UV 리소그래피를 이용하여 감광재 패턴을(pattern)을 만든다(Fig. 3b). 이어 건식 식각 공정(dry etching)을 이용하여 실리콘 웨이퍼의 <110> 결정면에 45° 각도로 Si₃N₄ 패턴을 만드는데(Fig. 3c), 이는 추후 실리콘 웨이퍼 상에 생성되는 단차의 경사 각도가 90°가 되게 하기 위함이다. Si₃N₄ 패턴이 만들어지면 감광제 패턴을 제거하고 Si₃N₄ 패턴을 마스크 삼아 실리콘 웨이퍼의 식각 공정을 수행한다(Fig. 3d). 이 때 식각 공정은 KOH(수산화칼륨) 수용액(30%, 45~50°C, 식각율: 100~200 nm/min)을 이용하여 이방성으로 진행되도록 한다. 마지막으로 건식 식각 공정 또는 인산을 이용하여 Si3N4 패턴을 제거하면 실리콘 웨이퍼 상에 90° 경사 각도를 갖는 미세 단차가 만들어진다(Fig. 3e). Fig. 3(f)는 이렇게 제작된 시편의 실제 모습(크기: 35 mm×17 mm×1 mm)을 보여 주는데 확대된 측면 모습을 보면 단차의 경사 각도가 90°임을 알 수 있다.

Fig. 3

Procedure for sample fabrication

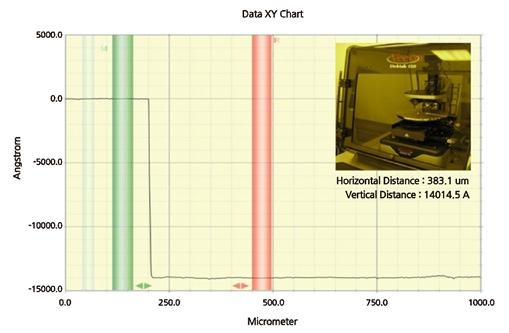
단차 높이는 Fig. 3(d)에서 식각이 이루어지는 시간을 조정함으로써 10 nm 이하의 정밀도로 제어할 수 있는데, 자극 세기에 대한 보다 정확한 수치 입력을 위해 제작된 샘플 전부에 대해 단차 높이가 측정되었다. 측정은 조도나 단차 측정에 특화된 접촉식 표면 윤곽측정기(surface profilometer, Veeco Dektak 150)를 이용하여 수행되었는데, 측정기의 수직 방향 분해능은 최대 1 Å(반복도는 6 Å 이하)이며 측정에 사용된 스타일러스(stylus)의 지름은 1.25 μm이다. Fig. 4는 표면윤곽측정기 Veeco Dektak 150의 모습 및 이를 통해 수행된 측정 결과의 예이다.

Fig. 4

Measurement of step height by the surface profilometer (Veeco Dektak 150)

3. 단차 인지 촉감 평가

단차 인지에 대한 촉감 평가는 예비 실험(pilot test)과 본 실험(main test) 두 단계로 수행되었다. 실험 방법으로는 예비 실험(pilot test)에서는 극한법(method of limits), 본 실험(main test)에서는 항상자극법(method of constant stimuli)을 이용하였다. 실험 수행 시에는 예비 실험과 본 실험 모두 피실험자들이 일상생활에 주로 사용하는 손가락의 끝을 사용하도록 하였으며, Fig. 5와 같이 가림막을 설치하여 시각적으로 단차를 인지하지 못하도록 하였다. 또한 단차 인지 여부에 대한 응답은 5초 이내에 하도록 하였다.

Fig. 5

Experimental scene

3.1 예비 실험(pilot test)

3.1.1 실험방법

예비 실험은 단차에 대한 절대 역치를 대략적으로 측정하여 본 실험에 사용될 시편의 단차 범위를 정하기 위해 수행되었으며, 실험 방법으로는 극한법이 사용되었다. 극한법(method of limits)은 자극들을 오름차순(상승법)이나 내림차순(하강법)으로 제시하여 자극이 인지되기 시작되는 수준(역치)을 측정하는 방법이다. 즉, 오름차순 실험에서는 자극의 강도를 높여가며 피실험자가 자극을 느끼기 시작하는 최소 강도를 찾고 내림차순 실험에서는 반대로 자극의 강도를 낮춰가며 피실험자가 자극을 느끼지 못하는 최대 강도를 찾는데 그 평균값이 ‘역치’에 해당된다.

본 연구에서 예비 실험은 20~35세 남녀 각각 5명(평균 30.6세, 표준편차 3.6세)을 대상으로 실시하였다. 실험에서 손가락 접촉은 Table 1과 같이 4가지 Mode로 수행되었으며, Kawamura, Tani & Yamada의 연구^[8]에서와 같이 주로 민감한 손의 검지 끝으로 자연스럽게 접촉하도록 하였다. 실험에 사용된 시편의 단차는 Table 2와 같이 Mode 1,2의 경우에는 7수준, Mode 3,4의 경우에는 5수준으로 주어졌다. 실험은 오름차순과 내림차순 각각 3회씩 무작위적으로 수행되었다.

Table 1

Experimental modes for the pilot test

Table 2

Sample sets for the pilot test

3.1.2 결과 및 분석

예비 실험에서는 5명의 피실험자에 대해 오름차순과 내림차순 각각 3회씩 반복 실험을 수행함으로써 각 Mode마다 30개의 데이터를 수집하였는데, 평균, 표준편차를 구한 결과가 Table 3에 주어져 있다. Table 4의 일원배치 분산분석의 결과를 살펴보면 F = 75.731, p = 0.000(유의수준: 0.05)으로 모드 간 통계적으로 유의한 차이가 있음을 알 수 있다. 모드 간 차이를 Duncan 사후 검정을 통해 살펴본 결과, Table 5에서와 같이 Mode 1과 2, Mode 3과 4는 각각 동일한 집단으로 묶임을 알 수 있었다. 즉, Mode 1과 2, Mode 3과 4 사이에는 각각 통계적으로 유의한 차이가 없음을 알 수 있었다.

Table 3

Absolute thresholds measured from the pilot test

Table 4

Result of the one-way ANOVA (Analysis of variance)

Table 5

Post-hoc test result

3.2 본 실험(main test)

3.2.1 실험방법

본 실험에는 25~35세 남녀 총 37명(남: 20명, 여: 17명, 평균 29.3세, 표준편차 2.2세)이 참여하였으며 실험 방법으로는 항상자극법(method of constant stimuli)이 사용되었다. 항상자극법을 이용하 여 단차에 대한 절대 역치를 측정하기 위해서는 단차의 높이가 등간격으로 배치된 시편들이 요구되는데, 실험에 사용된 단차의 높이는 예비 실험에서 구해진 역치의 평균값과 표준편차를 이용하여 구해졌다. 구체적으로는 Mode 별로 평균(μ) ± 2×표준편차(σ)를 본 실험을 위한 단차의 범위로 설정하고 이를 6개의 등간격으로 분할하여 7개의 서로 다른 단차 높이를 갖는 시편을 제작하였다. 이렇게 제작된 시편의 단차 높이는 Table 6과 같다. Table 6에서 Mode 2, 4에 대한 시편 set가 없는 이유는 앞서 예비 실험 결과 분석에서 언급했듯이 Mode 1과 2, Mode 3과 4 사이에는 절대 역치 값에 유의한 차이가 없어 본 실험에는 둘 중 Mode 1과 Mode 3에 대해서만 실험을 수행하기로 결정하였기 때문이다.

Table 6

Sample sets for the main test

실험은 피실험자들로 하여금 주로 사용하는 손의 검지 끝을 사용하여 시편을 접촉하도록 한 후 단차인지 여부를 ‘Yes’ 나 ‘No’ 만으로 답하게 하는 방식으로 진행되었다. 피실험자에게는 하나의 시편을 평가하는데 약 5초가 주어졌으며, Mode 별로 7개의 시편이 10회씩 무작위로 제시되었다.

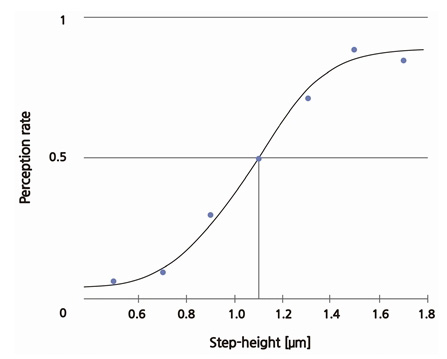
다음 Fig. 6은 피실험자가 단차 인지 여부에 대한 질문에 ‘Yes’로 답한 비율을 7개의 시편에 대해 나타낸 그래프인데 가로축은 단차의 높이를, 세로축은 ‘Yes’ 응답 비율을 나타낸다. Fig. 6에서 단차 인지 여부에 대한 ‘Yes’ 응답 비율은 단차의 높이가 커짐에 따라 증가하는 양상을 보이는데, 정신물리학에서 이는 통상 정규분포함수의 누적곡선을 따르게 된다. 이러한 심리 측정 곡선에서 인지율이 0.5가 되는 자극의 세기가 절대 역치에 해당하는데, 그 값은 Fig. 6에서와 같이 실험 결과에 부합하는 최적의 정규분포함수를 구한 후 그 평균값을 취함으로써 얻을 수 있다.

Fig. 6

Psychometric curve for step perception

3.2.2 결과 및 분석

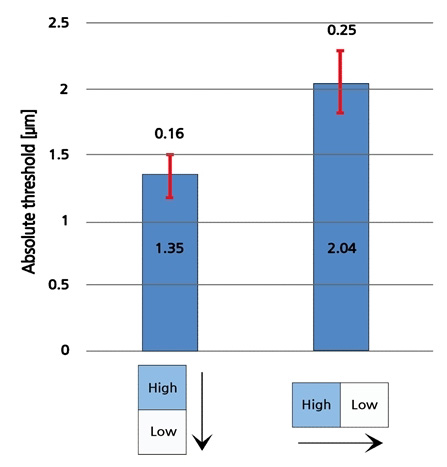
본 실험 결과에 대한 분석은 본 실험에 참여한 37명의 데이터 중 정규성 여부에 대해 부적합 판정을 받는 16명의 데이터를 제외한 21명(남10/여11)의 데이터를 토대로 이루어졌다. 이 경우 2가지 Mode 중 하나라도 정규성 검증을 통과하지 못한 피실험자의 데이터는 분석에서 일괄 배제되었다. 결과적으로 피실험자 21명, Mode 종류 2가지, 시편 7종, 시편 당 반복횟수 10회를 인자로 하는 총 2940개(21×2×7×10)의 데이터가 분석에 사용되었다. 앞서 기술된 심리 측정 곡선을 활용한 절대 역치 구하는 법을 이 데이터에 적용하여 피실험자 별로 역치를 구하였다. 전체 피실험자에 대해 Mode 별로 평균과 표준 편차를 구한 결과가 Fig. 7과 Table 7에 주어져 있는데, Mode 1, 3에 대한 평균값이 각각 1.35 μm, 2.04 μm로 예비 실험을 통해 구한 값(Mode 1: 1.33 μm / Mode 3: 2.02 μm)과 유사함을 알 수 있다. Table 8은 Mode 간 유의한 차이가 있는지 알아보기 위해 독립표본 t 검정을 수행한 결과인데, 통계량 t = -10.782, p=0.000 (유의수준<0.05)으로 Mode 간에 유의한 차이가 있음을 알 수 있다.

Fig. 7

Absolute thresholds measured from the main test

Table 7

Group Statistics

Table 8

Independent Sample t-test

4. 결 론

본 연구에서는 예비 실험(극한법 이용)을 통해 본 실험(항상자극법 이용)을 위한 계획(시편의 단차 범위, 평가 Mode 선정 등)을 세우고, 본 실험을 통해 경사 각도가 90°인 단차에 대한 절대 역치를 구하였다. 실험의 결과를 분석한 결과 다음과 같은 결론을 내릴 수 있었다.

∙ 손가락을 단차의 높은 면에서 낮은 면으로 움직일 때와 낮은 면에서 높은 면으로 움직일 때의 단차 인지에 대한 절대 역치 의 유의미한 차이는 없다.

∙ 손가락을 손가락 방향과 동일한 방향으로 움직일 때(Mode1)와 손가락 방향과 수직인 방향으로 움직일 때(Mode3)의 단차 인지에 대한 절대 역치의 유의미한 차이가 있으며, 그 값은 각각 1.35 μm와 2.04 μm이다.

단차 인지에 있어 보다 민감한 반응을 보이는 Mode 1의 절대 역치를 이용하여 99%의 사람들이 인지하지 못하는 단차의 높이를 구하면 그 값은 약 1.25 μm (1.35 - (t_20,99 × 0.16 / √21) = 1.25, t_20,99 = 2.845)가 된다. 이 값은 제품 표면에 존재하는 단차에 대한 불량 판정의 기준이 될 수 있으리라 판단된다. 하지만 제품 성형 시 만들어지는 단차의 높이를 이 값 이하로 제한하는 것은 현실적으로 힘들다. 따라서 단차 유발 요인을 디자인 단계에서 원천적으로 배제하거나, 생성되는 단차의 형상이 완만한 경사면이나 곡면을 갖도록 성형 공정이나 후처리 공정을 제어할 필요가 있다. 이를 위해서는 단차의 형상이 절대 역치에 미치는 영향을 추가적으로 조사할 필요가 있다. 다른 한편으로는 손가락 접촉 Mode에 따라 절대 역치가 달라진다는 결과를 활용하여 정보를 전달하는 수단으로 단차를 활용하는 방안을 생각해 볼 수 있다. 예를 들어, 단차의 높이를 Mode 1과 Mode 3으로부터 구해진 절대 역치의 중간값으로 설정하면 단차의 경사 방향이 손가락 방향에 수직일 때는 단차가 인지되지 않으나 손가락 방향과 동일할 때는 단차가 인지된다. 따라서 시각을 이용하지 않고도 촉각만으로 평면이 놓인 방향을 인지할 수 있다. 따라서 추가적인 연구를 통해 이를 디자인적 요소로 활용하는 방안을 찾는 것이 요구된다.

Acknowledgments

이 연구는 서울과학기술대학교 교내 학술연구비 지원으로 수행되었습니다.

References

• Johanson, R. S., Lamotte, R. H., (1983), Tactile Detection Thresholds for a Single Asperity on an otherwise Smooth Surface, Somatosensory Research, 1(1), p21-31.
• LaMotte, R. H., Whitehouse, J., (1986), Tactile Detection of a Dot on a Smooth Surface: Peripheral Neural Events, Journal of neurophysiology, 56(4), p1109-1128. [https://doi.org/10.1152/jn.1986.56.4.1109]
• LaMotte, R. H., Srinivasan, M. A., (1991), Surface Microgeometry: Tactile Perception and Neural Encoding, In Information Processing in the Somatosensory System, ( Tactile Perception and Neural Encoding, In Information Processing in the Somatosensory System,), p49-58, Palgrave London. [https://doi.org/10.1007/978-1-349-11597-6_4]
• Kawamura, T., Ohka, M., Miyaoka, T., Mitsuya, Y., (1996), Measurement of Human Tactile Sensation Capability to Discriminate Fine Surface Textures Using a Variable Step-Height Presentation System, In 5th IEEE International Workshop on Robot and Human Communication (RO-MAN 1996), p274-279. [https://doi.org/10.1109/ROMAN.1996.568845]
• Kawamura, T., Otobe, Y., Tani, K., (2009), Effect of Touching Manner and Motion Direction of Human Finger on Human Tactile Recognition, In 5th IEEE International Workshop on Robot and Human Communication(RO-MAN 2009), p998-1003. [https://doi.org/10.1109/ROMAN.2009.5326238]
• Ohka, M., Kawamura, T., Miyaoka, T., Mitsuya, Y., (2000), Human Tactile Sensation Capability for Moving Fine Step-Heights,  Transactions of the Japan Society of Mechanical Engineering(Series C), p226-231. [https://doi.org/10.1299/kikaic.66.226]
• Kawamura, T., Tanaka, N., Tani, K., (2012), Directionality of Human Tactile Sense of Fingertip in Discriminating Fine Step-heights, International Journal of Social Robotics,  4(1), p67-76. [https://doi.org/10.1007/s12369-012-0149-8]
• Kawamura, T., Tani, K., Yamada, H., (2012), Measurement System of Fine Step-Height Discrimination Capability of Human Finger’s Tactile Sense, In Advanced Topics in Measurements, InTech. [https://doi.org/10.5772/37513]