프레스 기계의 불평형 관성력 계산과 진동 해석

2.1 관성력 계산

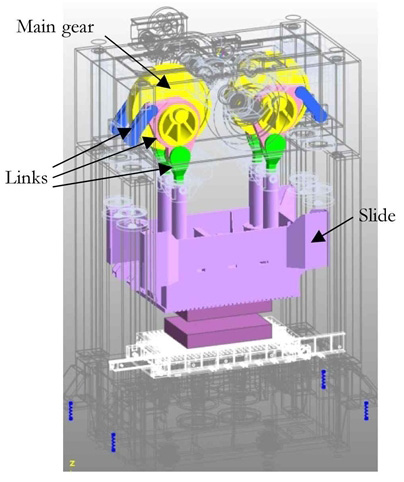
본 연구에서 해석하고자 하는 프레스는 Fig. 1 과 같이 상부 구동부에 구동 모터와 클러치, 동력전달 기어, 감속기로 구성되어 프레스 동력을 전달한다. 프레스 형식은 기계식 편심 프레스 방식이다. 감속기 기어에서 전달 받은 동력은 주 기어(Main Gear)의 중심에서 일정한 회전 속도를 가진 회전 운동을 발생시킨다. 주 기어의 회전 운동은 각 링크(Link)들로 연결된 기구들의 구속된 움직임에 의해 가공력을 발생시키는 슬라이드(Slide)의 수직 병진 운동으로 변환된다. 프레스를 수학적으로 모델링 한 Fig. 2에서 주 기어의 중심은 점 A와 같고 슬라이드는 점 F와 같다. 프레스의 주 기어는 15 RPM으로 운전된다.

Fig. 1

3d modeling of a press machine

Fig. 2

Mathematical modeling of a press machine for kinematic analysis

불평형 질량은 Fig. 1과 같이 수직 상하 운동 기구의 관성에 의해 발생하는 관성력이다. 이들 불평형 질량은 좌우 방향에서는 대칭으로 평형을 이루나 수직 방향으로는 불평형을 이루어 관성력에 의한 진동 하중을 발생시킨다.

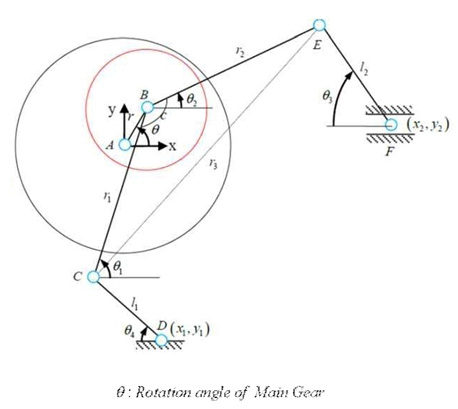
관성력의 크기와 이의 영향을 해석적으로 분석하기 위해 각 링크의 동역학적 변위 분석을 통해 전체 불평형 관성력의 크기를 계산한다. 이를 위해 Fig. 2와 같이 프레스를 옆으로 누인 모양을 xy좌표의 강체계로 모델링하였다. Fig. 2에서와 같이 구속조건이 정의되는 프레스의 각 설계 위치 A, B, C, D, E, F에 의해 각 링크의 길이 r, r₁, r₂, r₃, l₁, l₂가 결정된다.

먼저 프레스의 기구학적인 변위 관계식을 구한다. Fig. 2의 점 D의 x, y좌표, 점 F의 y좌표는 고정되어 있으므로 다음의 구속조건식이 얻어진다.

여기서 θ는 주 기어의 회전각이다. θ₁, θ₂, θ₃, θ₄는 각 링크들의 회전각이다.

Fig. 2에서 각 링크의 회전각은 다음과 같은 관계식을 가진다.

여기서

이다.

식 (1)~(4)로 나타나는 구속조건식의 해는 반복수행 수치해석 방법을 이용하여 구할 수 있다. 반복수행식의 증분 값은 다음 식과 같다.

여기서,

이다.

앞의 기구학적 수치해석 방법으로 주 기어의 회전각 θ = ωt로 주어지면 각 링크의 회전각 θ₁, θ₂, θ₃, θ₄를 구할 수 있다. 이를 통해 각 링크의 변위를 구할 수 있다.

슬라이드의 위치를 나타내는 점 F의 x좌표는 다음과 같다.

주 기어의 회전각 θ의 입력 값에 대해 전체 기구의 변위가 계산되면, 각 위치에서 전체 링크의 속도를 다음의 과정으로 구할 수 있다.

구속조건식 (1)~(4)를 미분하고 주 기어의 회전각속도 $$ \dot{\theta }=\omega $$[rad/s]를 대입하면 다음과 같이 된다.

위의 식으로부터 주 기어의 회전각속도 ω가 주어지면 각 링크의 각속도를 알 수 있고 슬라이드의 속도도 다음 식으로 구할 수 있다.

마지막으로 속도 관계식 (9)를 미분하면 가속도를 구할 수 있다. 각 링크의 회전각가속도는 다음 식과 같다.

슬라이드의 가속도는 다음과 같이 나타낼 수 있다.

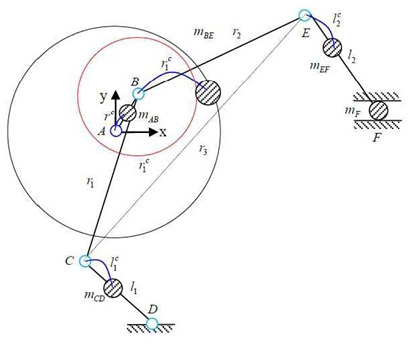
위에서 구한 각 부품에서의 변위, 속도, 가속도를 이용하여 각 부품의 관성력을 구할 수 있다. Fig. 3과 같이 각 링크의 질량 중심의 정보를 r^c, r₁^c, r₂^c, r₃^c, l₁^c, l₂^c로 나타내었다. 또한 각 링크의 질량 크기를 m_AB, m_BE, m_EF, m_CD, m_F로 표시하였다.

Fig. 3

Positions of the mass centers of the links

m_AB의 관성력은 다음과 같다.

m_BE의 관성력은 다음과 같다.

m_EF의 관성력은 다음과 같다.

m_CD의 관성력은 다음과 같다.

슬라이드를 나타내는 m_F의 위치와 관성력은 다음과 같다.

2.2 관성력 해석결과

앞에서 얻어진 프레스 기구의 수학적 모델링을 이용하여 슬라이드의 기구학적 특성과 각 링크의 불평형 관성력을 계산하고자 한다.

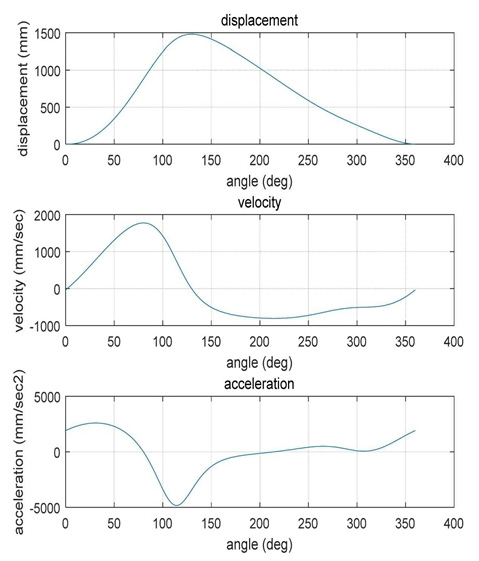
Fig. 4는 앞절의 계산식으로부터 구한 슬라이드의 수직방향 변위, 속도, 가속도를 나타낸다. 슬라이드의 변위로부터 프레스의 상사점과 하사점, 소성 가공과 귀환 위치를 결정하는 정보를 알 수 있다. 슬라이드는 최대 1,495 mm의 왕복운동을 통해 가공 행정을 하고 있다. 주 기어가 0°일 때 하사점, 129° 일 때 상사점으로 계산되었다. 이로부터 주 기어가 0~129°까지는 프레스는 가공 준비를 위한 귀환 행정, 129~360°까지는 가공 행정임을 알 수 있다.

Fig. 4

Displacement, velocity and acceleration of the slide vs. angle of the main gear

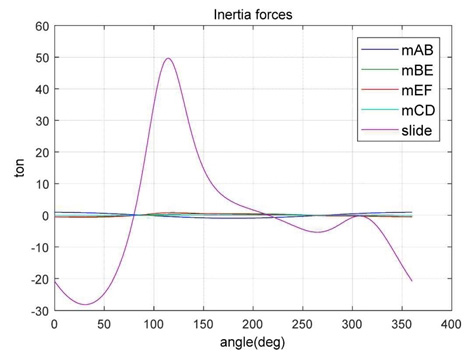
Fig. 5는 각 링크들의 불평형 질량 관성력을 주 기어의 각도에 따라 계산한 결과를 나타낸다. 각 링크들의 관성력은 슬라이드에 비해 무시할 수 있을 만큼 작은 것으로 나타났다. 이는 슬라이드의 질량이 상대적으로 크고 수직 방향 변위 변화가 가장 크기 때문인 것으로 판단된다.

Fig. 5

Inertial forces of the links vs. angle of the main gear

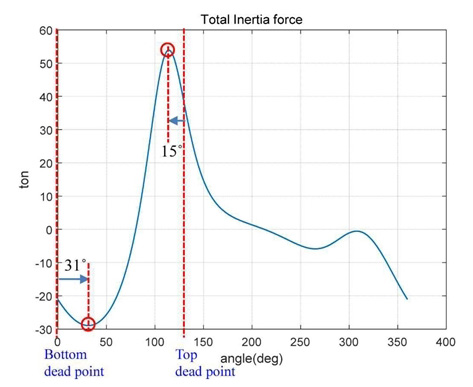
전체 관성력은 Fig. 6과 같이 하사점에서 주 기어가 31° 지난 위치에서 하단 방향으로 최소값 -29 ton으로 나타났다. 상사점 위치 15° 전에 상단 방향으로 최대값 54 ton으로 계산되었다. 관성 변동량은 83 ton으로 계산된다. 이를 통해 프레스 기계의 관성에 의한 가진력의 변동 크기는 83 ton임을 알 수 있다. 또한 귀환 행정 내에서 불평형 관성력이 최대값 및 최소값으로의 변동하는 것으로 나타났다. 가공 충격력이 발생하는 가공 행정이 아니라 귀환 행정에서 불평형 관성력이 최대 및 최소값의 변동을 가지므로 가공 충격력에 관성력의 주요한 변동이 겹쳐지지 않으므로 진동 가진력에는 유리한 것으로 분석되었다.

Fig. 6

Total inertial force and dead points vs. angle of the main gear

3.1 관성력 가진 진동

위의 각 링크의 관성력은 불평형 질량으로서 프레스의 진동원으로 작용한다. 이들 불평형력 진동원을 외력으로 가정하여 1자유도계 진동을 해석한다.

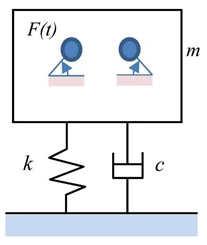
Fig .7은 프레스 불평형 관성력을 진동원으로 하는 1자유도계 진동계를 보여준다. 불평형 질량 관성력 F(t)는 비조화 운동이므로 수치적분을 통해 해를 구할 수 있다. 프레스의 몸체인 Bed의 수직 방향 변위 z(t)는 다음과 같이 계산된다.

Fig. 7

1 d-o-f forced vibration system of the press machine

여기서, ω_d는 감쇠고유진동수, ω_n은 비감쇠 고유진동수, m은 프레스 전체 질량, ζ는 감쇠비를 의미한다.

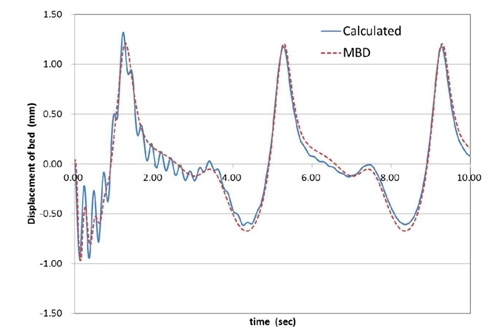
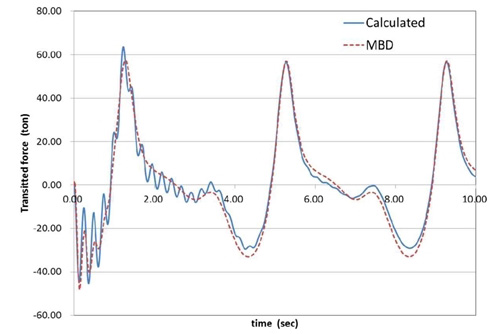
프레스는 15 RPM으로 운전되며 이는 4초의 주기 운동에해당된다. 프레스는 이와 같은 주기가 정해진 운동이므로 시간 영역에서 진동 응답을 해석하였다. Fig. 8과 Fig. 9는 프레스의 수직방향 변위 z(t)와 바닥 전달력의 크기를 보여주고 있다. 해석 결과는 상용 다물체 동역학 해석 프로그램인 Recurdyn의 해석 결과와 비교하였다. 다물체 동역학 해석에서 진동계 모델링과는 달리 프레스의 각 링크는 3차원 강체로 모델링되고 주 기어의 구동에 의해 실제 물리계와 유사하게 결과가 얻어진다. 다물체 동역학 해석결과와 동일한 결과를 나타냄으로써 본 연구에서 제시한 불평형 관성 계산식의 타당성을 검증할 수 있었다.

Fig. 8

Comparison of the calculated bed displacement with multibody dynamics analysis

Fig. 9

Comparison of the calculated transmitted force with multibody dynamics analysis

Fig. 8에서 프레스의 수직 방향 변위는 정상상태에서 1.24 mm ~ -0.56 mm로 변화함을 알 수 있다. Fig. 9에서 프레스 바닥에 전달되는 외력은 정상상태에서 86 ton이 변동하는 것으로 나타났다. 관성력의 변동이 83 ton이므로 이 보다 조금 큰 값으로 바닥 전달력이 변동되는 것으로 계산되었다.

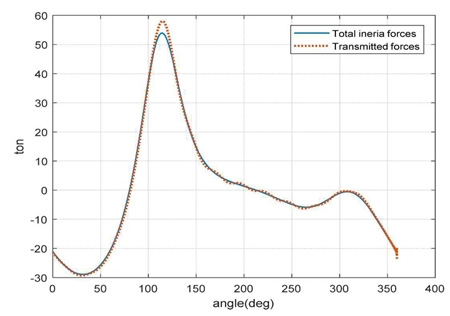
Fig. 10은 정상상태에서 주 기어의 회전 값에 대한 불평형 관성력과 바닥 전달력을 비교한 그림이다. 바닥 전달력은 불평형 관성력과 거의 동일한 위상과 크기로 변동되고 있음을 보여 준다.

Fig. 10

Total inertial force vs. transmitted forces

3.2 설계 인자 영향 분석

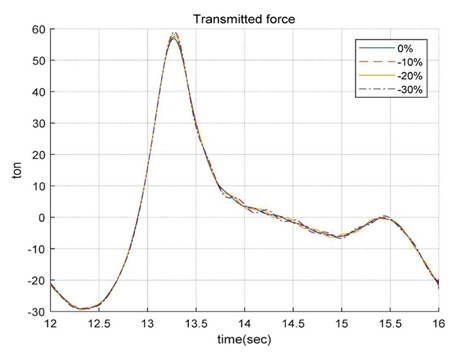
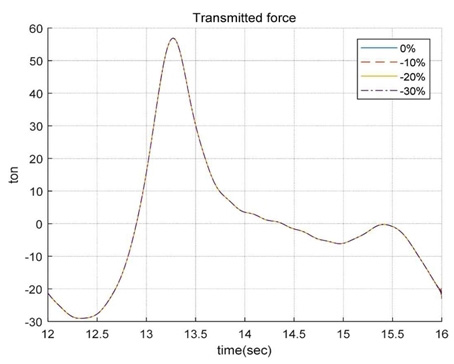
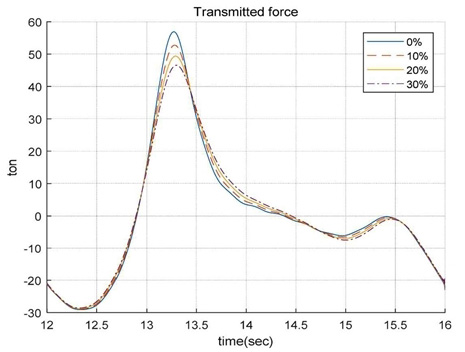
프레스 지지계의 스프링 및 감쇠 특성이 바닥 전달력에 미치는 영향을 비교해 보았다. 각 파라미터를 0~30%까지 10%씩 감소한 결과를 Fig. 11, Fig. 12에 나타내었다. 지지계의 스프링 및 감쇠의 특성 변화가 바닥 전달력에는 영향이 미소함을 알 수 있다.

Fig. 11

Influence of stiffness on the transmitted force

Fig. 12

Influence of damping on the transmitted force

부품의 기하학적 설계 위치를 변화시킬 때 바닥 전달력의 차이를 알아보기 위해 변위 제한 링크의 설계위치인 점 C와 점 D의 위치를 변화시키며 바닥 전달력의 변동 값을 구해 보았다. 점 C와 점 D의 위치의 범위 값을 30%까지 10%씩 변화하면서 이 범위 내에서 바닥 전달력을 최소화하는 최적화 과정을 수행하였다. 이때, 가공 특성에 영향을 미치는 슬라이드의 변위의 변동 값은 일정하게 유지하기 위해 이 값은 제한 조건 값으로 하였다. 이를 수식화하면 다음과 같다.

여기서, F_T는 바닥 전달력이며, x₂는 슬라이드의 변위이다.

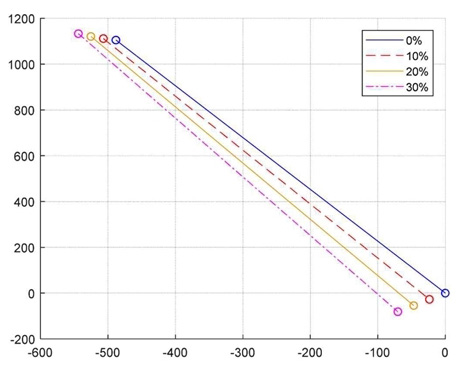
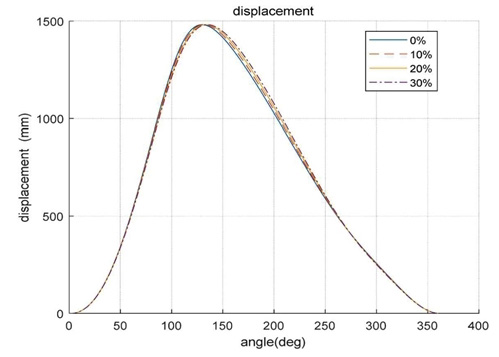
Fig. 13은 변경 범위 내에서 최적 위치로 계산된 점 C와 점 D의 이동위치를 나타낸다. Fig. 14와 Fig. 15는 각 위치에서 바닥 전달력과 슬라이드의 변위를 나타낸다. Fig. 14와 같이 설계 위치의 범위를 키울수록 바닥 전달력은 감소한다. 이때 Fig. 15와 같이 슬라이드 변위는 유지됨을 알 수 있다. 링크의 설계 위치를 변경함으로써 지지부의 강성이나 감쇠보다 효과적으로 전달력을 감소시킬 수 있는 것으로 나타났다.

Fig. 13

Changes of positions of points C and D for optimization

Fig. 14

Influence of design geometries on the transmitted force

Fig. 15

Influence of design geometries on the displacement of the slide