대형 공작기계용 스핀들-베어링 시스템의 동적 특성 및 피로수명에 관한 연구

1. 서 론

공작기계의 스핀들은 가공 성능을 결정하는 가장 중요한 요소 중 하나이다. 공작기계의 스핀들은 최근 제조업의 고도화와 복합화에 의해 고정밀, 고속화가 요구되고 있으며 성능 예측에 기초한 설계가 더욱 중요해지고 있다^[1]. 스핀들의 특성을 사전에 파악한다면 제품의 정밀도와 완성도에 영향을 줄 수 있는 문제를 원천적으로 배제할 수 있게 되며, 특히 베어링 타입과 배열, 피로수명, 발열 등을 고려한 실용적 설계가 가능하게 된다^[1-3].

스핀들은 사용 목적에 따라 다양한 형태가 존재하는데, 그 중 고속, 정밀 가공의 목적을 가진 스핀들의 경우는 각접촉 볼베어링(Angular contact ball bearing, ACBB)을 주로 채택하고 있다. 각접촉 볼베어링은 축방향과 경방향의 복합하중을 동시에 지지하고 고속 및 정밀도를 유지할 수 있기 때문에 공작기계 스핀들에 널리 이용된다. 그러나 각접촉 볼베어링은 경방향 하중, 회전속도 등의 작동조건에 의해 그 특성이 변화되는 것으로 알려져 있어 작동조건에 따른 특성 예측이 필요하다^[4-6]. 특히, 각접촉 볼베어링 특성에 결정적 영향을 미치는 접촉각은 예하중, 회전속도 등에 의해 변화하게 된다. 또한 가공 중에 발생하는 절삭 하중에 의한 경방향 하중은 베어링의 특성에 복잡한 영향을 주게 된다^[4].

우수한 스핀들 설계를 위해서는 앞서 언급한 회전속도, 경방향 하중 등, 가능한 모든 영향 요인을 고려하여 시스템 특성을 합리적으로 예측해야 한다. 그러나 이러한 예측 결과를 활용한 설계를 하기 위해선 복잡한 계산 과정과 많은 시간, 비용이 소요되는 검증 작업이 필요하다. 이런 문제를 개선하기 위해 많은 연구자들에 의해 보다 정확한 베어링 특성과 스핀들 모델링 및 해석 방법에 관한 연구가 이루어졌다. Bae^[5] 등은 공작기계의 가공 정밀도에 크게 영향을 미치는 회전속도에 따른 스핀들의 돌출량을 예측하였고, Song^[6] 등은 고속으로 회전하는 스핀들의 베어링 강성 변화와 스핀들의 고유진동수 변화에 대해 연구하였다. Gagnol^[7] 등은 고속 회전하는 스핀들의 회전속도에 따른 동적 특성 변화를 계산하였고, 실험을 통해 가공 중인 스핀들의 모드 해석을 수행하였다.

스핀들 설계에 대한 연구도 다양하게 발표되어 왔다. Park^[8]은 진동 특성을 고려한 공작기계 초고속 스핀들 설계를 위해 스핀들 구동 조건에 따른 베어링의 종류와 윤활 방법을 분석하고 이에 따른 스핀들 강성과 진동 특성 해석 연구를 수행하였다. Lee^[9] 등은 굽힘 곡선을 이용하여 공작기계 스핀들의 정적, 동적 취약부 규명 방법을 제시하고 이에 따른 구조 개선을 연구하였다. Maeda^[10] 등은 스핀들 설계를 위해 개발한 프로그램을 통해 채터(Chatter) 진동이 없는 절삭 조건을 만족할 수 있도록 스핀들의 베어링 간격을 최적화하는 방법을 제안하였고, Huang^[11] 등은 다양한 베어링으로 지지되는 스핀들의 동적 응답에 대한 연구를 제시하였다. 또한 Kim^[12] 등은 공작기계용 40,000 rpm 스핀들의 정·동적 특성 해석과 최적 설계를 통해 스핀들 설계 시 고려해야 할 핵심인자들을 선정하고 최적 설계 안을 도출하였다.

스핀들의 고속화로 인해 발생하게 된 발열에 관한 연구도 다양하게 발표되어 왔다. Lee^[13] 등은 고속 유정압 스핀들의 개발을 위한 유정압 베어링의 최적화 실험을 통해 10,000 rpm의 고속회전 시에 온도 변화와 회전 정밀도를 확인하였다. Ko^[14] 등은 구름 베어링과 Air-oil 윤활, Built-in 모터로 구성되는 스핀들 작동 시 발생하는 열원의 수학적 모델과 전도 열전달, 대류 열전달의 합리적 경계조건을 설정하고 열적 거동 시뮬레이션을 통해 해석적으로 규명하였다.

Lee^[15]는 스핀들의 수명과 신뢰성 평가를 실시하였으며, Cao^[16] 등은 스핀들-베어링 계를 수학적으로 모델링하고 이를 통해 베어링과 스핀들의 회전 효과를 계산하였다. 또한 계산 결과와 안정도 선도를 이용하여 채터 현상을 예측할 수 있는 실험을 수행하였다.

Brecher^[17] 등은 고속 회전 시에 베어링 배열을 변화시키면서 공작기계의 스핀들의 강인성을 증가시키고, 수정된 실린더 롤러 베어링을 사용하여 고속에서의 베어링의 성능을 개선하는 연구를 진행하였다. Choi와 Hong^[18]은 스핀들 계에 경방향 하중이 가해질 때의 동특성 변화를 예측하는 방법을 제안하고 검증하였다.

스핀들의 특성에 결정적 영향을 미치는 구름 베어링에 대한 연구도 다양하게 진행되어 왔다. Bae^[19] 등은 각어긋남이 있는 각접촉 볼베어링의 피로수명 예측 방법을 개발하였다. Tong과 Hong^[20]은 스핀들 계에 널리 사용되는 복열 각접촉 볼베어링의 모델링 방법을 제안하였다. 최근에는 Hong과 Tong^[21]에 의해 구름 베어링의 모델링 및 해석 방법과 그 응용에 대한 그간의 연구성과 및 동향이 소개된 바 있다.

이상의 연구들은 고속 스핀들 시스템 또는 베어링의 회전속도, 예하중 등에 따른 특성 변화에 치중되어 있으며 많은 베어링으로 지지되는 대형 스핀들에 대한 연구나, 가공 중 발생하는 경방향 하중에 의한 스핀들 특성 변화 등에 관련 연구는 많지 않다. 특히 스핀들의 관리 운영 등을 위해 필요한 피로수명에 관한 연구는 매우 제한적이다.

본 논문에서는 많은 수의 각접촉 볼베어링을 채용한 대형 복합 가공기 용 스핀들 시스템 특성을 해석하였다. 특히 회전속도 및 경방향 하중이 스핀들의 정적 동적 특성과 피로수명에 미치는 영향을 분석하였다. 이를 위해 베어링 모델과 스핀들-베어링 모델을 구성하고 계산 결과를 실험 및 카탈로그^[22-24]와 비교하여 검증하였다. 또한 베어링을 사용하는 시스템의 설계 및 제조에서 가장 중요한 기준 중 하나인 베어링의 피로 수명을 ISO의 기본수명식을 이용하여 계산하였다. de Mul의 베어링 모델^[25]에 회전 효과를 고려한 수정된 베어링 모델을 시스템 모델링 및 해석에 사용하였다. 또한 베어링 모델과 회전체 유한요소모델을 결합하여 스핀들-베어링 계의 특성과 베어링의 피로수명을 계산할 수 있는 자체개발 프로그램을 사용하였다. 그리고 이를 실제 제작된 시스템의 고유진동수를 계산하고 실험과 비교하여 검증하였다. 개발된 모델을 활용하여 스핀들 베어링 계 관련 변수를 변화시킬 때 스핀들-베어링 계의 특성 변화와 베어링 피로수명에 미치는 영향을 분석하였다.

2. 대형 공작기계용 스핀들-베어링 모델링

본 연구에서는 대형 공작기계에서 사용되는 스핀들-베어링 계를 고려하였다. Fig. 1은 고려하고 있는 대형 공작기계와 스핀들-베어링 계를 보여준다. 축방향 및 경방향의 복합하중을 동시에 지지할 수 있는 3가지 종류의 각접촉 볼베어링(SKF 71948, SKF 71944, SKF 7022)이 총 12개 채용되었다. 이와 같이 여러 개의 베어링으로 지지되는 스핀들은 힘평형식으로부터 반력을 결정할 수 없는 부정정계(Statically indeterminate system) 특성을 보이기 때문에 회전속도와 경방향 하중으로 인한 특성 변화를 예측하기 쉽지 않다^[3]. 본 연구에서는 베어링을 모델링 하기 위해 de Mul의 모델^[25]을 수정하여 사용하였고, 스핀들 모델은 유한요소 운동방정식^[3]을 이용하였다. 또한 부정정계 특성을 해석하기 위해 반복 해법을 적용하였다. 본 절에서는 스핀들-베어링 계에서 운동 방정식을 구성하고 그 해를 구하는 과정을 간략하게 기술하였다.

Fig. 1

A large machine tool and the schematic diagram of the spindle-bearing system

2.1 베어링 모델

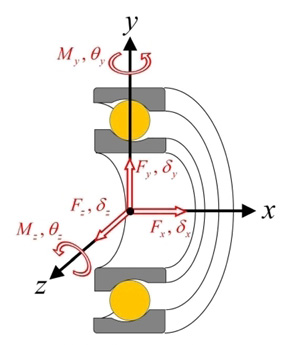
베어링의 강성은 내륜 중심점을 기준으로 외부에서 인가되는 힘과 모멘트에 대한 변위를 통해 계산된다. Fig. 2는 5 자유도 준정적 베어링 모델을 보여주고 있으며, 베어링 하중과 변위 벡터는 다음과 같이 나타낼 수 있다.

Fig. 2

Five degrees of freedom ACBB model with loading and displacement

$\[ \begin{array}{l}\left\{F\right\}={\left\{F_x F_y F_z M_Y M_z\right\}}^T\\ \left\{\delta \right\}={\left\{{\delta }_x {\delta }_y {\delta }_z {\gamma }_y {\gamma }_z\right\}}^T\end{array} \]$

(1)

베어링 강성 행렬은 각각의 베어링에 인가되는 하중과베어링 반력의 평형식을 푸는 과정을 통해 얻을 수 있으며, 하중벡터에 대한 변위벡터의 미분으로 다음과 같이 표시된다.

$\[ \left[k\right]=\left[\frac{\partial \left\{F\right\}}{\partial {\left\{\delta \right\}}^T}\right]=\left[\begin{array}{c}{k}_{xx}\\ k_{yx}\\ k_{zx}\\ k_{{\theta }_{y}x}\\ k_{{\theta }_{z}x}\end{array}\begin{array}{c}{k}_{xy}\\ k_{yy}\\ k_{zy}\\ k_{{\theta }_{y}y}\\ k_{{\theta }_{z}y}\end{array}\begin{array}{c}{k}_{xz}\\ k_{yz}\\ k_{zz}\\ k_{{\theta }_{y}z}\\ k_{{\theta }_{z}z}\end{array}\begin{array}{c}{k}_{x{\theta }_y}\\ k_{y{\theta }_y}\\ k_{z{\theta }_y}\\ k_{{\theta }_y{\theta }_y}\\ k_{{\theta }_z{\theta }_y}\end{array}\begin{array}{c}{k}_{x{\theta }_z}\\ k_{y{\theta }_z}\\ k_{z{\theta }_z}\\ k_{{\theta }_y{\theta }_z}\\ k_{{\theta }_z{\theta }_z}\end{array}\right] \]$

(2)

베어링 모델을 이용하면 피로수명계산에 필요한 구름 요소들의 접촉 하중 분포를 같이 계산할 수 있다. ACBB 모델의 세부 사항은 다른 여러 연구에서 찾을 수 있다^[2,3,19-21].

2.2 스핀들-베어링 모델

스핀들-베어링 계의 특성 해석을 위해 유한요소해석을 사용한 운동방정식을 다음과 같이 쓸 수 있다^[3].

$\[ \left[M^S\right]\left\{\ddot{q}\right\}+\left\{\Omega \left[G^3\right]\right\}\left\{\ddot{q}\right\}+\left\{\left[K^S\right]+\left[K^b\right]\right\}\left\{\ddot{q}\right\}=\left\{f\right\} \]$

(3)

여기서 [M^s], [G^s], [K^s]는 각각 스핀들 축 계의 질량, 자이로, 강성행렬이며, [K^b]는 스핀들을 지지하는 베어링에 의한 강성행렬을 의미한다. 또한, Ω는 축 회전속도를 의미하며, 전역좌표벡터 및 힘 벡터는 수평과 수직변위를 고려하여 다음과 같이 표현된다.

$\[ \begin{array}{cc}\left\{q\right\}=\left\{\begin{array}{c}y\\ z\end{array}\right\},& \left\{f\right\}=\left\{\begin{array}{c}{f}_y\\ f_z\end{array}\right\}\end{array} \]$

(4)

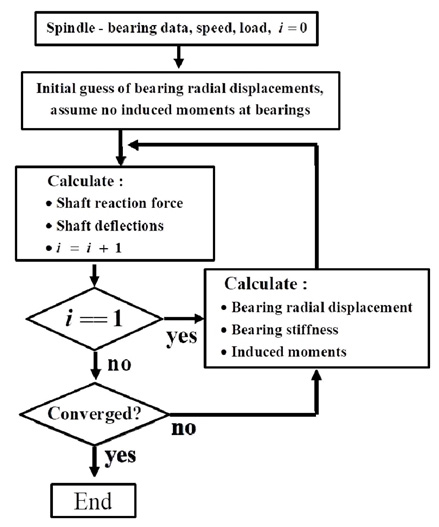
Fig. 3은 경방향 하중을 받는 경우의 스핀들과 베어링 특성을 계산하는 과정을 설명하고 있다. 스핀들에 경방향 하중이 가해지는 경우 베어링 하중이 힘평형식만으로 결정되지 않고 스핀들의 변형과 연계해서 결정된다^[26]. 이 문제를 해결하기 위해 반복해법을 이용한다. 먼저 경방향 하중을 고려하지 않은 경우의 베어링 강성을 계산하여 이를 초기치로 설정, 베어링 위치 별 반력을 계산한다. 계산을 통해 결정된 베어링 하중을 이용하여 베어링 강성을 결정하고 그 결과를 힘-평형 방정식과 힘-변형 방정식에 대입하여 반력을 다시 계산하는 과정을 수렴할 때까지 반복적으로 수행한다^[3].

Fig. 3

Overall calculation procedure of spindle-bearing system equilibrium equation[3]

3. 스핀들 베어링 모델 검증

본 연구에서 제안한 모델의 타당성을 검증하기 위해 베어링 제작 회사에서 제공하는 데이터를 이용하여 비교 검증하였다. 또한, 스핀들-베어링 계의 모델은 실험 결과와의 비교를 통해 검증하였다.

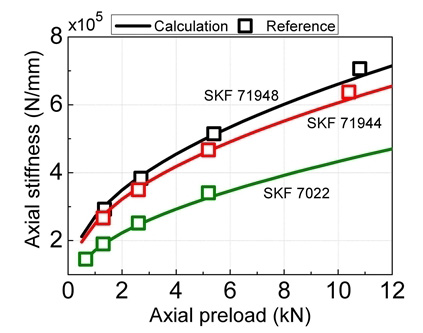
Fig. 4는 사용된 베어링 모델을 검증하기 위해 SKF 사에서 제공하는 카탈로그의 축방향 강성과 계산된 강성 결과를 비교하여 보여주고 있다. 그림에서 보이는 것과 같이 제안한 모델과 카탈로그 상의 축방향 강성이 잘 일치하는 것을 확인할 수 있다. 예하중이 증가함에 따라 베어링의 축방향 강성이 증가함을 확인할 수 있는데 이는 베어링 볼의 접촉면적이 증가하며 생기는 현상이다. 경방향 강성에 대해서도 이와 유사한 결과를 얻을 수 있다.

Fig. 4

Axial stiffnesses of ACBBs as a function of preload

3.2 스핀들 베어링 모델 검증

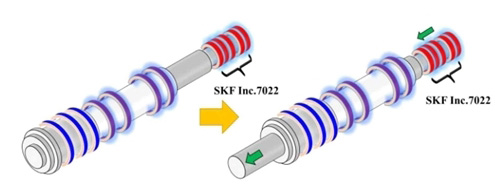
실험 대상인 대형 공작기계용 스핀들은 중공축(Hollow shaft) 내부에 축방향으로 이동 가능한 중실축(Solid shaft) 퀼(Quill)이 중첩된 구조로 구성되며, Fig. 5에 나타낸 바와 같이 SKF 7022 베어링 세트로 지지된 퀼(Quill)이 축방향으로 움직여 돌출하는 것이 가능하다. Fig. 6은 스핀들의 고유진동수 측정을 위한 실험의 구성과 측정된 주파수 응답 함수(FRF)를 보여준다. 스핀들 고유진동수 측정을 위해 충격실험을 수행하였다. 스핀들이 정지상태일 때 퀼의 돌출 위치에 따른 수직방향의 고유진동수를 측정하였다.

Fig. 5

Movement of the quill in the axial direction

Fig. 6

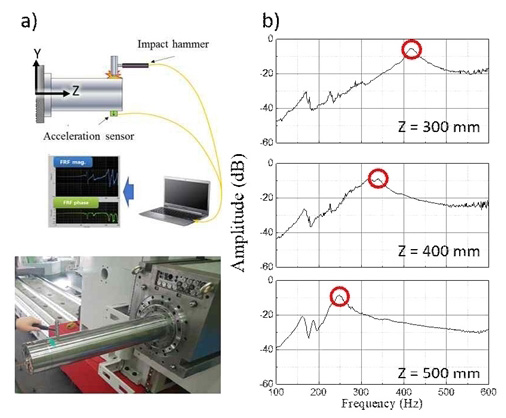
Impact test for the quill in the vertical direction: (a) experimental setup, (b) FRFs with varying quill position

Fig. 6(b)의 주파수응답함수로부터 스핀들의 고유진동수를 결정하였으며 퀼이 돌출됨에 따라 고유진동수가 낮아짐을 확인할 수 있다. Table 1에서 퀼 위치에 따른 고유진동수 측정결과와 제안한 모델의 계산결과를 비교하였다. 계산과 실험 결과가 대체로 잘 일치하고 있으나 계산이 약간 크게 나타나는 주 원인은 중실축과 중공축이 결합되는 부분을 중실축만으로 모델링함으로써 축 간 접촉부분의 강성 저하 효과가 반영되지 않았기 때문으로 추정된다.

Table 1

Comparison between calculation and measurement for fundamental natural frequency

이상과 같이 개발된 스핀들-베어링 계의 모델이 실험 결과와 유사한 결과를 보여주고 있으므로 스핀들-베어링 계의 특성을 해석하는데 유용함을 확인할 것으로 판단된다.

4. 스핀들-베어링 계의 동적 특성 해석

스핀들의 동적 특성은 스핀들의 안정적 운영을 위해 매우 중요하다. 본 절에서는 앞서 개발 검증한 스핀들 베어링 모델을 이용하여 동적 특성에 회전속도와 경방향 하중 등 운전 조건이 미치는 영향에 대해 분석하였다.

4.1 회전속도의 영향

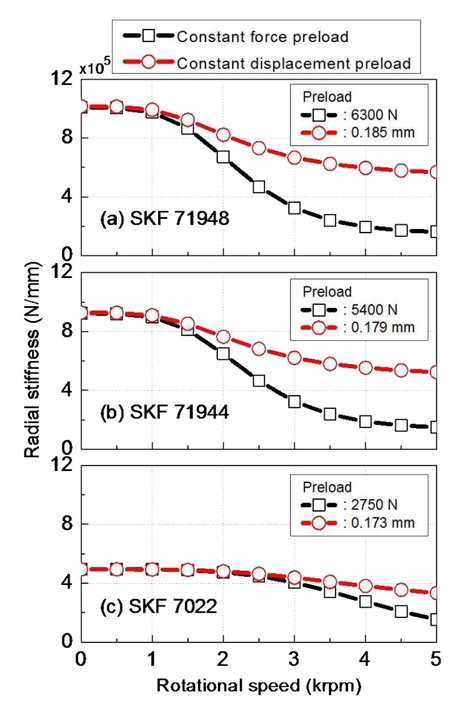
Fig. 7은 스핀들에 사용된 3가지 종류의 베어링에 대한 예하중 인가 방식과 회전속도에 따른 경방향 강성 변화를 나타낸다. 시뮬레이션은 경방향 하중이 없는 조건에서 수행되었으며, 그림에서 볼 수 있는 바와 같이 회전속도가 증가할수록 베어링 강성이 낮아지는 것을 확인할 수 있다. 예하중 인가 방식에 따라 강성의 변화 정도가 다르며, 정위치 예하중 방식이 접촉각 변화를 억제하는 효과가 있어 정예하중 방식에 비해 상대적으로 적은 변화를 보여준다.

Fig. 7

Radial stiffness variation as a function of rotational speed for two preload methods

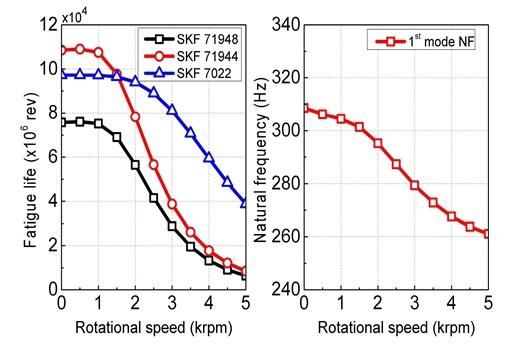
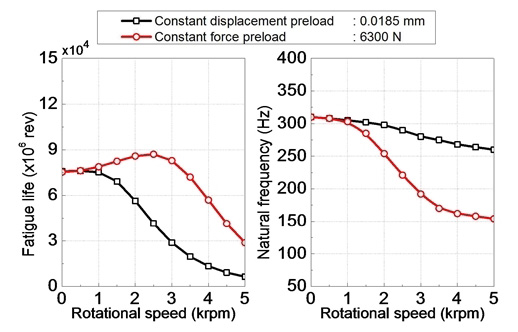
Fig. 8은 회전속도에 따른 베어링의 피로수명과 스핀들의 1차 고유진동수를 나타낸다. 본 시스템에서는 정위치 예하중을 사용하였다. 회전속도가 증가할수록 베어링의 피로수명과 스핀들 고유진동수가 모두 낮아지는 것을 확인할 수 있다. 특히, 1,000~3,000 rpm 사이에서 SKF 71948과 SKF 71944의 피로수명과 고유진동수가 급격히 감소한다. 이는 SKF 71948과 SKF 71944는 SKF 7022에 비해 더 크므로, 회전효과에 의한 영향을 더 크게 받기 때문이다.

Fig. 8

Basic rating lives of ACBBs and spindle natural frequency as a function rotational speed

그림에서 보여주는 바와 같이 SKF 71948은 피로 수명이 가장 작을 뿐만 아니라 스핀들 앞 부분에 위치하게 되어 가공 시 받게 되는 경방향 하중에 가장 크게 노출된다. 따라서 전체 시스템의 설계에 있어 피로수명은 SKF 71948을 기준으로 보는 것이 타당하다고 판단된다.

4.2 경방향 하중의 영향

가공 시 스핀들-베어링 시스템에 부가되는 절삭하중은 베어링에 직접적으로 인가되지 않고 축을 통해서 간접적으로 적용된다. 대상 시스템의 경우, 절삭 가공 중에는 일반적으로 퀼을 이동하지 않은 Z=0 mm인 상태에서 가공을 수행한다. 가공 중 발생하는 절삭하중에 의해 베어링에 간접적으로 작용하는 경방향 하중은 Fig. 1의 F_r로 표시된 것 과 같이 인가된다. 여기서는 경방향 하중에 대한 스핀들 시스템 특성 변화를 해석하였다.

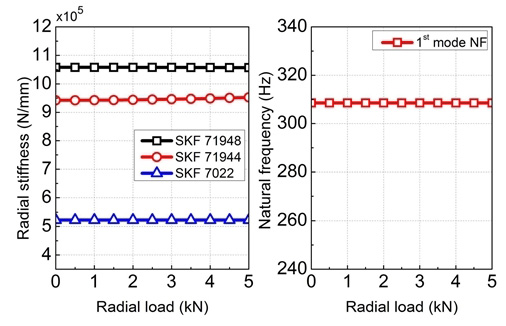
Fig. 9는 정지상태에서 0~5 kN의 경방향 하중을 인가하였을 때의 베어링의 경방향 강성과 스핀들의 고유진동수를 보여준다. 그림을 통해 경방향 하중에 따른 베어링 강성과 스핀들 고유진동수의 변화가 매우 미소한 것을 확인할 수 있다. 이는 베어링의 부하용량이 상대적으로 크고, 하중을 지지하는 베어링의 개수가 많기 때문에 경방향 하중 영향이 미미하게 나타나기 때문인 것으로 파악된다.

Fig. 9

Bearing stiffnesses and spindle natural frequency as a function of radial load (n=0 rpm)

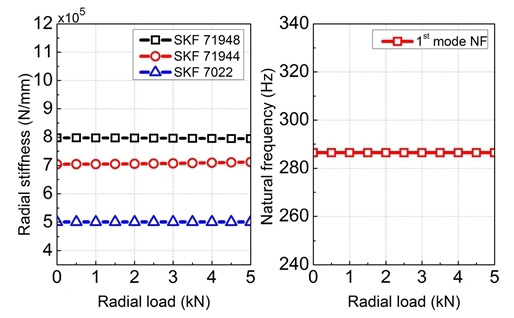
Fig. 10은 대상 대형 공작기계의 최대회전속도인 2,500 rpm 조건에서 경방향 하중에 따른 베어링의 강성과 스핀들의 1차 고유진동수를 보여준다. 정지상태와 비교하여 회전속도에 의한 영향으로 베어링 강성과 고유진동수가 낮아졌지만 경방향 하중에 의한 영향은 미미함을 확인할 수 있다. 본 공작기계에서 예상되는 최대 절삭하중이 1.5~2 kN임을 감안하면 실제 베어링에 작용하는 경방향 하중은 이보다 더 적을 것으로 판단된다. 따라서, 본 스핀들의 경우 베어링 강성과 고유진동수가 경방향 하중에는 큰 영향을 받지 않는 것으로 예상된다.

Fig. 10

Bearing stiffnesses and spindle natural frequency as a function of radial load (n=2,500 rpm)

5. 스핀들 베어링 계의 피로수명 해석

스핀들의 수명은 궁극적으로 베어링 수명에 의해 결정된다. 따라서 베어링의 피로수명 예측은 스핀들 계의 안정적 운영을 보장하는 데 중요하다. 특히 베어링의 유지보수 및 교체 계획 수립을 위해 정확한 피로수명 예측이 중요하다. 이러한 피로수명에 영향을 미치는 요인을 파악하기 위해 회전속도, 경방향 하중, 베어링 배열, 베어링 위치, 예하중 방식에 따른 시뮬레이션을 수행하였다. 해석 대상으로는 앞서 언급한 바와 같이 피로수명이 가장 낮게 평가되는 SKF71948을 고려하였다.

5.1 회전속도와 경방향 하중의 영향

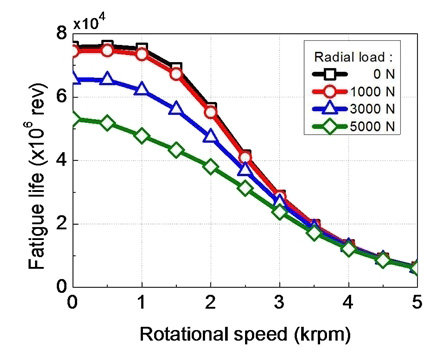
Fig. 11은 경방향 하중과 회전속도에 따른 베어링 SKF 71948의 피로수명을 나타낸다. 그림에 나타난 바와 같이 저속 영역에서는 경방향 하중이 증가할수록 피로수명이 크게 감소하지만 고속 영역에서는 경방향 하중의 영향이 낮아지고 있다. 이는 베어링이 고속으로 회전할수록, 베어링의 회전효과로 인해 발생하는 접촉력의 비중이 경방향 하중에 의해 발생하는 접촉력의 비중보다 상대적으로 커지기 때문이다.

Fig. 11

Fatigue life of SKF 71948 #3 as a function of rotational speed for different radial loads

대상 시스템의 최대회전속도 2,500 rpm에서 베어링 피로수명은 경방향 하중보다는 회전속도에 의한 영향을 크게 받고 있으나, 낮은 회전속도에서는 경방향 하중도 고려해야 함을 알 수 있다.

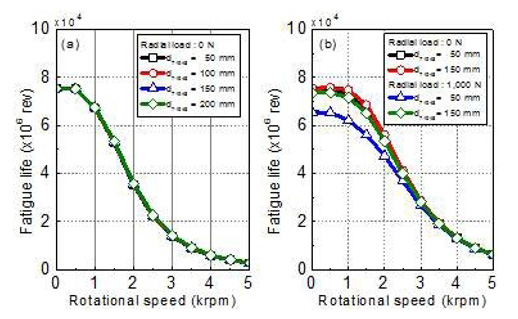
5.2 베어링 위치의 영향

Fig. 12는 베어링 위치에 따른 SKF 71948의 피로수명 해석 결과를 보여주고 있다. 여기서 베어링 위치는 베어링 사이의 간격을 의미한다. Fig. 12(a)는 베어링 SKF 71948 간의 간격에 따른 피로수명을 나타낸 것이고, Fig. 12(b)는 베어링 SKF 71948 간의 간격과 경방향 하중에 따른 피로수명을 나타낸다. 그림에서 볼 수 있듯이 경방향 하중이 없는 경우에 베어링 위치는 피로수명에 거의 영향을 미치지 않는다. 그러나 Fig. 12(b)에서 경방향 하중이 인가된 경우, SKF 71948의 위치 변화에 따라 베어링 하중의 변화가 발생하여 피로수명이 영향을 받는 것을 확인할 수 있다. 이는 축에 인가되는 외부 하중에 의해 베어링의 반력들이 영향을 받기 때문이다. 따라서, 경방향 하중에 따른 베어링 반력의 확인이 필요함을 알 수 있다.

Fig. 12

Fatigue life of SKF 71948 #3 according to bearing location (a) without radial load, (b) with radial load

5.3 베어링 배열의 영향

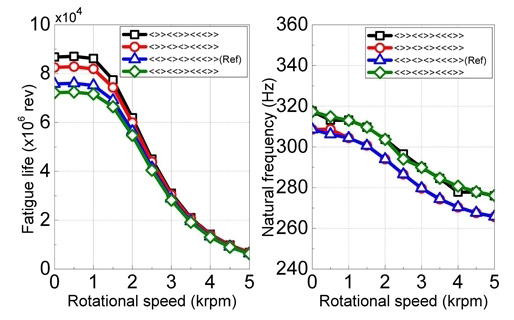
베어링 배열의 변화는 실효적 하중 작용 위치와 지지 방향 등에 영향을 주어 베어링 피로수명의 변화를 야기한다. 이는 배열에 따라 식 (2)에 포함된 성분 중 커플링 강성(k_yθz, k_zθy, k_zyθ, k_θzy)의 부호가 달라지기 때문이다. 이 같은 변화는 베어링이 위치한 곳의 경방향 변위와 연동되어 스핀들의 운동을 억제하거나 강화하는 방향으로 작용하고 시스템 특성에 영향을 미치기 때문에 베어링 배열 또한 설계에 고려될 중요한 요소이다^[2].

Fig. 13은 서로 다른 4가지 베어링 배열에 따른 SKF 71948의 피로수명을 나타낸다. 그림에서 현재 대상 시스템에 적용된 배열인 “<<><><><<<>>”보다 다소 높은 피로수명과 고유진동수를 얻을 수 있는 배열이 있음을 확인할 수 있다. 베어링 배열은 스핀들 초기 설계에서 결정해야 할 인자로서 사후 변경이 불가하므로 사전에 베어링 배열에 대한 점검을 한다면 스핀들의 피로수명 및 고유진동수 개선에 활용할 수 있을 것으로 판단된다.

Fig. 13

Fatigue life of SKF 71948 #3 and natural frequency according to bearing arrangement

5.4 베어링 예하중의 영향

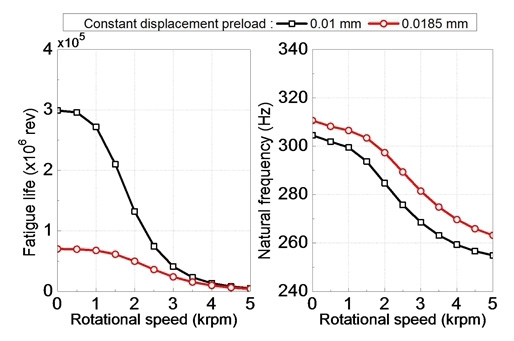
Fig. 14는 SKF 71948의 예하중에 따른 피로수명을 나타낸다. 정위치 예하중을 기존보다 낮게 인가하였을 경우, 3,000 rpm 이하의 회전속도에서 피로수명은 크게 증가한다. 이는 예하중을 낮게 인가함으로 인해 베어링 볼에 작용하는 하중이 줄어들기 때문이다. 그러나 낮은 예하중으로 인해 고유진동수가 전체적으로 낮아지게 된다. 이러한 특성을 고려할 때 예하중을 적절히 선정하여 적정한 피로수명과 고유진동수를 확보할 필요가 있다.

Fig. 14

Fatigue life of SKF 71948 #3 and natural frequency with preload changed

Fig. 15는 예하중 방식에 따른 베어링의 피로수명과 스핀들 고유진동수를 나타낸다. 운전속도 2,500 rpm에서 정예하중 방식의 피로수명이 정위치 예하중 방식보다 매우 크게 나타난다. 반면, 스핀들의 고유진동수는 매우 낮게 나오는 것을 확인할 수 있다. 이는 정예하중 방식에서 회전에 의한 베어링 강성 변화가 상대적으로 크게 나타나기 때문이다. 한편, 정예하중 방식에서 회전속도 중가에 따라 수명이 증가하였다가 급격히 감소하는데, 이는 저속에서는 원심력에 의해 내륜의 접촉력이 감소하여 수명이 증가하다가 속도가 커지면 외륜과의 접촉력 증가가 더 큰 영향을 미치기 때문이다.

Fig. 15

Fatigue life of SKF 71948 #3 and natural frequency for two different preloading methods

결론적으로, 피로수명보다 고유진동수가 더 중요한 설계 조건이 되는 경우에는 정위치 예하중 방식을, 그 반대의 경우에는 정예하중 방식을 채택하는 것이 바람직함을 알 수 있다.

6. 결 론

본 연구에서는 여러 개의 각접촉 볼베어링으로 지지되는 대형 스핀들의 동특성과 베어링 피로수명에 대해 논의하였다. 이를 위해 스핀들-베어링 모델과 해석 기술을 개발하였고 이를 업체 제공 데이터 및 실험과의 비교를 통해 검증하였다. 개발/검증된 모델을 이용한 시뮬레이션을 통해 스핀들의 동특성과 피로수명에 대해 분석하였다. 대상 스핀들의 경우 동특성과 피로수명 모두 회전속도에 큰 영향을 받게 되나 가공에 의해 발생하는 경방향 하중의 경우 피로수명에 주로 영향을 미치게 된다. 본 연구를 통해 제시한 결과는 개발 시스템의 안정적 운영과 향후 개선된 모델을 제작하는 데 유용하게 활용될 수 있을 것으로 판단된다.

Acknowledgments

본 논문은 한국산업기술진흥원이 지원하는 경제협력권 산업육성 사업 중 기흥기계㈜ 총괄로 수행한 ‘주축헤드 자동교환장치를 부착한 150톤 이상의 대형 복합가공기 개발’ 과제 연구결과의 일부입니다.

References

• Abele, E., Altintas, Y., Brecher, C., (2010), Machine Tool Spindle Unit, CIRP Annals Manufacturing Technology, 59, p781-802. [https://doi.org/10.1016/j.cirp.2010.05.002]
• Hong, S. W., Choi, C. S., Lee, C. H., 2013), (Effects of Bearing Arrangement on the Dynamic Characteristics of High-speed Spindle, Effects of Bearing Arrangement on the Dynamic Characteristics of High-speed Spindle, Journal of the Korean Society for Precision Engineering, 30(8), p854-863.
• Tong, V. C., Bae, G. H., Hong, S. W., (2015), Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types, Journal of the Korean Society for Precision Engineering, 32(2), p117-125. [https://doi.org/10.7736/kspe.2015.32.2.117]
• Jorgensen, B. R., Shin, Y. C., (1998), Dynamics of Spindle-bearing Systems at High Speeds Including Cutting Loads Effects, ASME, Journal of Manufacturing Science and Technology, 120(2), p387-394.
• Bae, G. H., Lee, C. H., Hwang, J. H., Hong, S. W., (2012), Estimation of Axial Displacement in High-speed Spindle Due to Rotational Speed, Journal of the Korean Society for Precision Engineering, 29(6), p671-679. [https://doi.org/10.7736/kspe.2012.29.6.671]
• Song, J. S., Lee, K. J., Gil, B. S., Lee, H. J., Ha, H. P., (2013), Rotor-dynamics Analysis of Machine Tool Spindle with Bearing Varying Stiffness, Proceedings of the KSPE Spring Conference, p225-226.
• Gagnol, V., Le, T. P., Ray, P., (2011), Modal Identification of Spindle-tool Unit in High-speed Machining, Mechanical Systems and Signal Processing, 25(7), p2388-2398. [https://doi.org/10.1016/j.ymssp.2011.02.019]
• Park, B. Y., (1991), Development of High Speed Machine Tool Spindle Regarding Vibration Characteristics, Journal of the Korean Society for Precision Engineering, 9(3), p149-156.
• Lee, C. H., Lee, H. S., (1998), Static and Dynamic Weak Point Analysis of Spindle Systems Using Bending Curve, Journal of the Korean Society for Precision Engineering, 15(12), p188-193.
• Maeda, O., Cao, Y., Altintas, Y., (2005), Expert Spindle Design System, International journal of Machine tools and Manufacture, 45(4-5), p537-548. [https://doi.org/10.1016/j.ijmachtools.2004.08.021]
• Huang, B. W., Kung, H. K., (2003), Variations of Instability in a Rotating Spindle System with Various Bearings, International Journal of Mechanical Sciences, 45(1), p57-72. [https://doi.org/10.1016/s0020-7403(03)00039-0]
• Kim, D. H., Lee, C. M., Choi, H. J., (2013), Static and Dynamic Analysis and Optimization Design of 40,000rpm High-speed Spindle for Machine Tools, Trans. Korean Soc. Mech. Eng. A, 37(1), p105-111. [https://doi.org/10.3795/ksme-a.2013.37.1.105]
• Lee, C. S., Moon, H. M., Cho, Y. K., Cho, H. T., Baek, Y. J., Chae, S. S., Lee, J. C., (2006), A Study on the Development of Hydrostatic High Speed Spindle for Nano CNC Grinding Machine, Proceedings of the KSMPE Autumn Conference, p228-233.
• Ko, T. J., Hwang, P., Kim, H. S., (1995), An Analysis of the Thermal Behavior of a High Speed Machine Tool Spindle, Proceedings of the KSMTE Spring Conference, p9-16.
• Lee, T. H., (2014), A Study on the Failure and Life Assessment of High Speed Spindle, Journal of the Korean Society for Precision Engineering, 31(1), p67-73. [https://doi.org/10.7736/kspe.2014.31.1.67]
• Cao, Y., Altintas, Y., (2007), Modeling of Spindle-bearing and Machine Tool Systems for Virtual Simulation of Milling Operations, International Journal of machine tools and manufacture, 47(9), p1342-1350. [https://doi.org/10.1016/j.ijmachtools.2006.08.006]
• Brecher, C., Spachtholz, G., Paepenmüller, F., (2007), Developments for High Performance Machine Tool Spindles, CIRP Annals-Manufacturing Technology, 56(1), p395-399. [https://doi.org/10.1016/j.cirp.2007.05.092]
• Choi, C. S., Hong, S. W., (2013), Study on Dynamic Characteristics of Spindle-bearing System Subjected to Radial Load, Journal of the Korean Society of Manufacturing Technology Engineers, 22(4), p740-746. [https://doi.org/10.7735/ksmte.2013.22.4.740]
• Bae, G. H., Tong, V. C., Hong, S. W., (2016), Fatigue Life Analysis for Angular Contact Ball Bearing with Angular Misalignment, Journal of the Korean Society for Precision Engineering, 33(1), p53-61. [https://doi.org/10.7736/kspe.2016.33.1.53]
• Tong, V. C., Hong, S. W., (2017), Analysis of the Stiffness and Fatigue Life of Double-Row Angular Contact Ball Bearings, Journal of the Korean Society for Precision Engineering, 34(11), p813-821. [https://doi.org/10.7736/kspe.2017.34.11.813]
• Hong, S. W., Tong, V. C., (2016), Rolling-element Bearing Modeling: A Review, Int. J. Precis. Eng. Manuf., 17(12), p1729-1749.
• SKF 71948 ACD/P4A, viewed 10), Aug, (2017, SKF: Angular contact ball bearings, super-precision, <http://www.skf.com/group/products/bearings-units-housings/super-precision-bearings/angular-contact-ball-bearings/acbb-skf-high-and-super-precision/index.html?designation=71948%20ACD>.
• SKF 71944 ACD/P4, viewed 10), Aug, (2017, SKF: Angular contact ball bearings, super-precision, <http://www.skf.com/group/products/bearings-units-housings/super-precision-bearings/angular-contact-ball-bearings/acbb-skf-high-and-super-precision/index.html?designation=71944%20ACD>.
• SKF 7022 ACD/P4A, viewed 10), Aug, (2017, SKF: Angular contact ball bearings, super-precision, <http://www.skf.com/group/products/bearings-units-housings/super-precision-bearings/angular-contact-ball-bearings/acbb-skf-high-and-super-precision/index.html?designation=7022%20ACD>.
• de Mul, J. M., Vree, J. M., Maas, D. A., (1989), Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom While Neglecting Friction-Part II: Application to Roller Bearings and Experimental Verification, Journal of Tribology, 111(1), p149-155. [https://doi.org/10.1115/1.3261865]
• Hong, S. W., Kang, J. O., Shin, Y. C., (2002), Dynamic Characteristics of Indeterminate Rotor Systems with Angular Contact Ball Bearings Subject to Axial and Radial loads, International Journal of Precision Engineering and Manufacturing, 3(2), p61-71.