다각형 블록으로 구성된 케이블구동시스템의 운동특성

1. 서 론

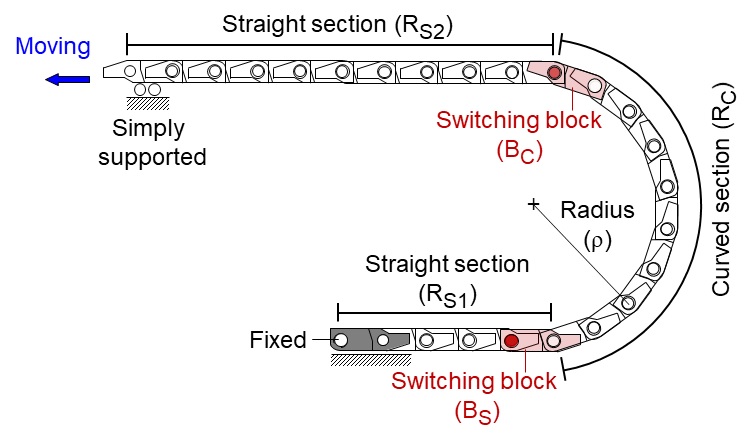
이동하는 장비에 전력을 공급하는 케이블은 이송 시스템에 의해 장비와 같이 이동한다. 이러한 케이블이송시스템에 요구되는 조건은 케이블의 자중을 지지할 수 있어야 한다는 것과 케이블 및 장비의 위치에 따라 그 형태가 직선에서 곡선으로 유연하게 변환될 수 있어야 한다는 것이다^[1]. Fig. 1과 같이 다각형 블록이 핀 조인트로 연결된 체인구동시스템은 변환 블록의 회전을 통해 직선 영역과 곡선 영역 사이의 형태 전환이 가능하고 동시에 다각형 형상에 따른 회전 범위의 제한을 통해 케이블 하중을 지지할 수 있는 횡방향 강성을 제공하기 때문에 각종 산업 현장의 이동 장비에 널리 활용되고 있다.

Fig. 1

Chain drive system with polygonal blocks

하지만 이러한 다각형 블록의 체인구동계는 일정한 속도로 이송되는 경우에도 직선에서 곡선으로 형태가 전환되는 지점에서는 속도의 변동이 발생하며 이는 롤러체인구동계에서 나타나는 다각형 효과(polygonal effect)처럼 계의 동적 거동에 많은 문제점을 야기할 수 있다^[2]. 이와 관련하여 롤러체인구동계에 대해서는 다각형 효과의 기하학적 모델링 방법에서부터^[3] 다물체동역학을 활용한 수치적 방법^[4], 축방향 및 횡방향의 동특성 분석 등^[5,6] 많은 연구들이 수행되어 왔다.

또한 축방향으로 이동하는 직선 보의 동특성에 관해서도 매우 많은 선행 연구가 있는데 외팔보의 횡방향 진동에 관한 이론 해석^[7], 단순지지보의 이동 속도에 따른 동적 안정성 분석^[8], 감쇠가 횡진동에 미치는 영향^[9], 외팔보로 단순화시킨 다각형체인구동계에서 동특성 분석^[10] 등에 관한 연구가 있다. 이 외에도 이동하는 곡선보의 파동 특성에 관한 연구가 있다^[11].

하지만 이러한 많은 선행 연구에도 불구하고 Fig. 1과 같은 체인구동계에서 다각형 효과에 의해 발생하는 운동 특성에 관해 수행된 연구는 아직 없다.

본 연구에서는 직선부와 곡선부로 구성된 다각형 체인구동계를 5절 기구로 단순화한 모델을 제시하고 운동학적 해석을 수행하여 블록 형상이 운동 특성에 미치는 영향을 분석하고자 한다. 또한 다물체동역학에 의한 수치해석을 통하여 그 결과를 검증하고자 한다.

2. 체인구동계의 운동학적 해석

2.1 다각형 블록의 체인구동계

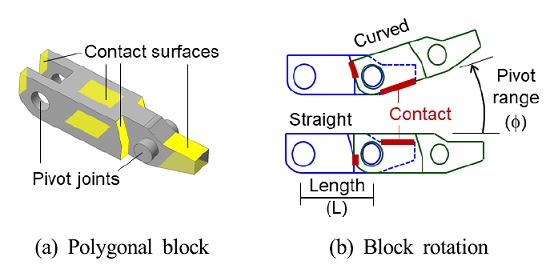
본 연구에서 대상으로 하는 다각형 블록의 체인구동시스템은 Fig. 1에 도시한 것처럼 직선부 R_S1과 R_S2, 곡선부 R_C로 이뤄지는 개루프 시스템이다. 다각형 블록은 Fig. 2(a)에 나타낸 바와 같이 다수의 접촉면과 핀 조인트로 구성되며 핀 조인트에서의 회전 범위 ϕ는 블록 길이 L과 곡률 반경 ρ에 따라 다음과 같이 결정된다.

Fig. 2

The geometry and pivot range of a polygonal block

$\[ \varphi ={\cos }^{-1}\left[1-\frac{1}{2}{\left(\frac{L}{\rho }\right)}^2\right] \]$

(1)

식(1)로 결정되는 회전 운동은 R_S1, R_S2의 끝단 블록인 B_S와 B_C에서만 일어나며 그 외의 모든 블록은 상호 간의 접촉에 의해 회전 운동이 구속된다. Fig. 2(b)에 나타낸 바와 같이 R_S2에 속한 블록들은 접촉면 C_T에 의해 회전없이 직선 운동을 하게 되고 R_C에 속한 블록들은 접촉면 C_B에 의해 회전없이 블록 사이의 각도 ϕ를 유지한 상태로 반경 ρ인 원주를 따라 이동하게 된다.

Fig. 1과 같이 R_S2의 끝단이 수평 구동되면 R_S1의 블록 B_S는 회전하기 시작하여 ϕ에 도달하면 회전을 멈추고 R_C의 블록으로 변환된다. 동시에 R_C의 블록 B_C는 회전을 통해 R_S2의 블록으로 변환되며 이러한 운동이 각 블록에 대해 순차적으로 반복된다.

따라서 R_S2 끝단이 일정한 속도로 구동될 경우 Fig. 1(a)의 시스템은 주기운동을 하며 매 주기마다 R_S1의 블록은 1개 감소하고 R_S2의 블록은 1개 증가하므로 구동계는 블록 길이의 2배에 해당하는 2L만큼 수평 이동한다.

2.2 단순화된 5절기구 모델에 의한 운동학적 방정식

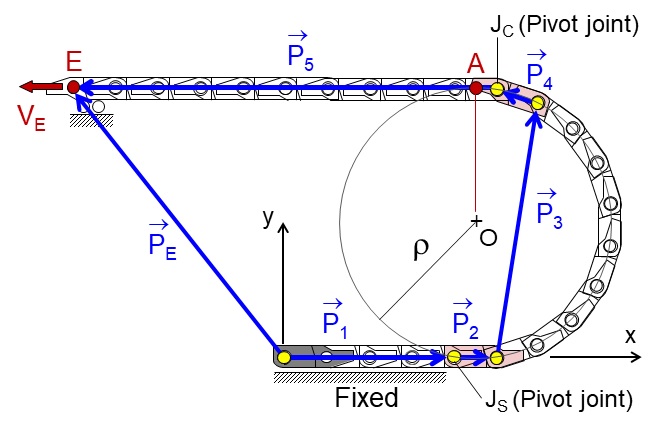
Fig. 3은 체인구동계의 운동학적 거동을 해석하기 위한 모델로서 블록 상호간의 회전 유무를 고려하여 5절기구로 단순화시켰다. 즉, 직선부 R_S1은 회전하지 않는 블록과 회전하는 변환 블록으로 나뉘므로 2개의 벡터 $$ {\overrightarrow{P}}_1$$과 $$ {\overrightarrow{P}}_2$$로 모델링하였으며 마찬가지로 곡선부 R_C도 $$ {\overrightarrow{P}}_3$$과 $$ {\overrightarrow{P}}_4$$로 모델링하였다. 반면에 직선부 R_S2는 모든 블록이 회전하지 않으므로 하나의 벡터 $$ {\overrightarrow{P}}_5$$로 나타냈다. $$ {\overrightarrow{P}}_1$$, $$ {\overrightarrow{P}}_2$$, $$ {\overrightarrow{P}}_4$$ 및 $$ {\overrightarrow{P}}_5$$의 크기는 실제 블록 길이와 동일하지만 $$ {\overrightarrow{P}}_3$$의 크기는 곡선부의 회전없는 블록 수 N_C로부터 식(2)와 같이 주어진다. 여기서 N_C는 식(3)을 만족하는 최대 정수로서 B_S의 반과 B_C를 고려한 것이다.

Fig. 3

Simplified kinematic modeling

$\[ P_3=\sqrt{2\left\{1-\cos \left(N_C\varphi \right)\right\}} \]$

(2)

$\[ N_C\le \frac{\pi }{\varphi }-1.5 \]$

(3)

이에 근거하여 Fig. 3의 구동계에 대한 해석 방정식은 다음과 같다.

$\[ \begin{array}{c}{P}_1+P_2{e}^{j{\theta }_2}+P_3{e}^{j{\theta }_3}+P_4{e}^{j{\theta }_4}\\ +P_5{e}^{j{\theta }_5}=P_{E_X}+j{P}_{E_Y}\end{array} \]$

(4)

여기서 $$ {\overrightarrow{P}}_2$$, $$ {\overrightarrow{P}}_3$$ 및 $$ {\overrightarrow{P}}_4$$는 상호 간에 회전이 없으므로 θ₃와 θ₄는 θ₂로부터 아래와 같이 구할 수 있다.

$\[ \begin{array}{ll}{\theta }_3={\theta }_2+\left(\frac{N_C+1}{2}\right)\varphi ;& {\theta }_4={\theta }_2+\left(N_C+1\right)\varphi \end{array} \]$

(5)

따라서 끝단 E의 위치가 주어지면 식(4), (5)로부터 θ₂, θ₃, θ₄ 및 θ₅를 구할 수 있으며 그 결과로부터 계의 위치 특성을 알 수 있다. 또한 식(4)의 미분을 통해서 구한 식(6)으로부터 계의 속도 특성을 구할 수 있다.

$\[ P_2{\omega }_2{e}^{j{\theta }_2}+P_3{\omega }_2{e}^{j{\theta }_3}{+P}_4{\omega }_2{e}^{j{\theta }_4}{+P}_5{\omega }_5{e}^{j{\theta }_5}=j{V}_E \]$

(6)

여기서 ω₂, ω₃ , ω₄ 및 ω₅는 $$ {\overrightarrow{P}}_2$$, $$ {\overrightarrow{P}}_3$$, $$ {\overrightarrow{P}}_4$$ 및 $$ {\overrightarrow{P}}_5$$의 각속도이다.

2.3 다각형 효과에 의한 2단계 주기운동

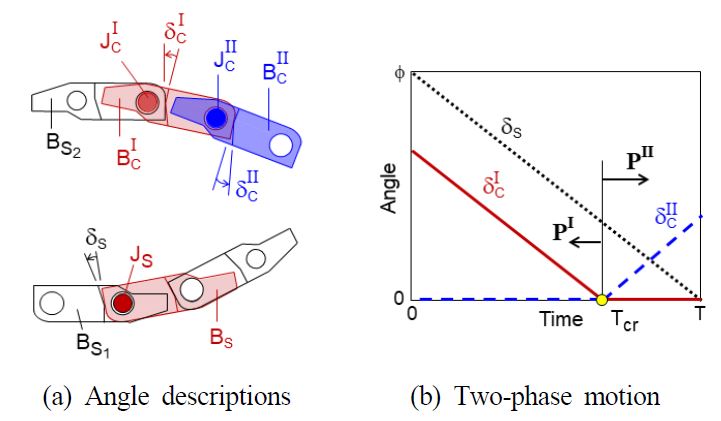
Fig. 1에서 변환 블록 B_S가 회전을 시작하는 시점부터 ϕ만큼 회전하는 시점까지를 체인구동계의 주기 T로 정의하고 주기 내 임의의 시각에서 변환 블록 B_S와 B_C의 회전 위상을 보면 Fig. 4(a)과 같다. 여기서 주목할 점은 두 블록의 회전 위상이 서로 동기화되지 않기 때문에 주기 운동은 상단의 변환 블록 기준으로 $$ B_C^I$$에서 회전이 일어나는 P^I 단계와 $$ B_C^{II}$$에서 회전이 일어나는 P^II 단계로 나뉜다는 점이다.

Fig. 4

Angular motion of the switching blocks

2단계 주기운동을 Fig. 4(a)의 블록 사이 각도로 살펴보면 다음과 같다. 주기 운동이 시작할 때 B_S와 이웃 블록 B_S1이 이루는 각 δ_S는 ϕ에서 출발하지만$$ B_C^I$$와 B_S2가 이루는 각 $$ {\delta }_C^I$$는 ϕ보다 작은 값에서 시작하며 그 크기는 블록 길이 L과 곡률 반경 ρ에 따라 결정된다. 결과적으로 $$ {\delta }_C^I$$는 Fig. 4(b)에 도시한 바와 같이 T_cr에 도달하는 순간 0이 되어 회전이 멈추게 되는데 이는 $$ B_C^I$$이 곡선부에서 직선부로 변환이 끝났다는 것을 의미한다. 따라서 임계시각 T_cr 이후에는 변환 블록이 $$ B_C^{II}$$로 바뀌게 되며 그로 인하여 곡선부의 블록 수 N_C가 1만큼 줄어들게 되고 식(2), (4), (5) 및 (6)의 파라미터 값들이 달라진다.

3. 체인구동계 주기운동의 특성 분석

3.2 주기운동의 변동 특성

다각형 블록의 체인 구동계는 블록 길이, 곡률 반경 및 끝단 이동속도에 따라 그 운동 특성이 달라진다. 본 연구에서는 곡률 반경 ρ를 70mm, 끝단 속도V_E를 -1 m/s로 고정시키고 블록 길이 L을 21.4~22.9mm 범위에서 0.5mm 간격으로 변화시키면서 계의 운동을 구했다.

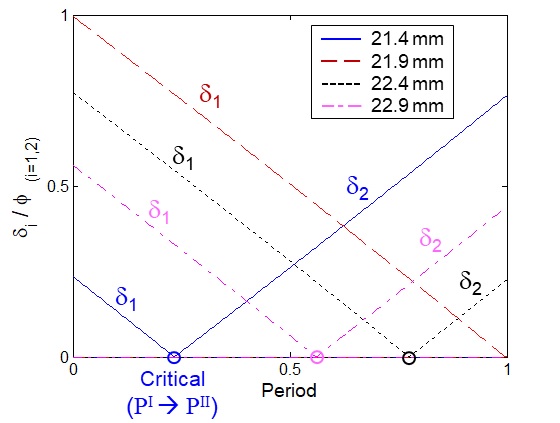
Fig. 5는 L과 임계 시각 T_cr의 관계를 블록 각도 δ₁과 δ₂의 변화로부터 구한 결과이다. L=21.9mm일 때는 주기운동의 초기 상태에서 δ₁이 블록의 회전범위 ϕ와 같은 경우로서 T_cr이 존재하지 않고 P^I단계의 주기 운동만이 일어난다. 반면에 L이 그 외의 값일 경우에는 T_cr이 존재하며 P^I에서 P^II로 바뀌는 2단계의 주기 운동이 일어난다.

Fig. 5

Angular motion of the upper switch blocks during one period vs. block length

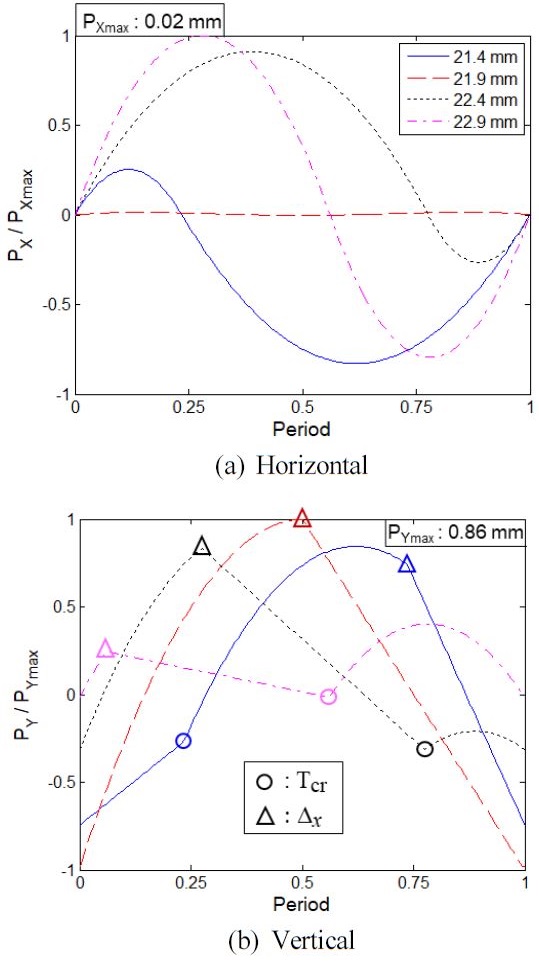
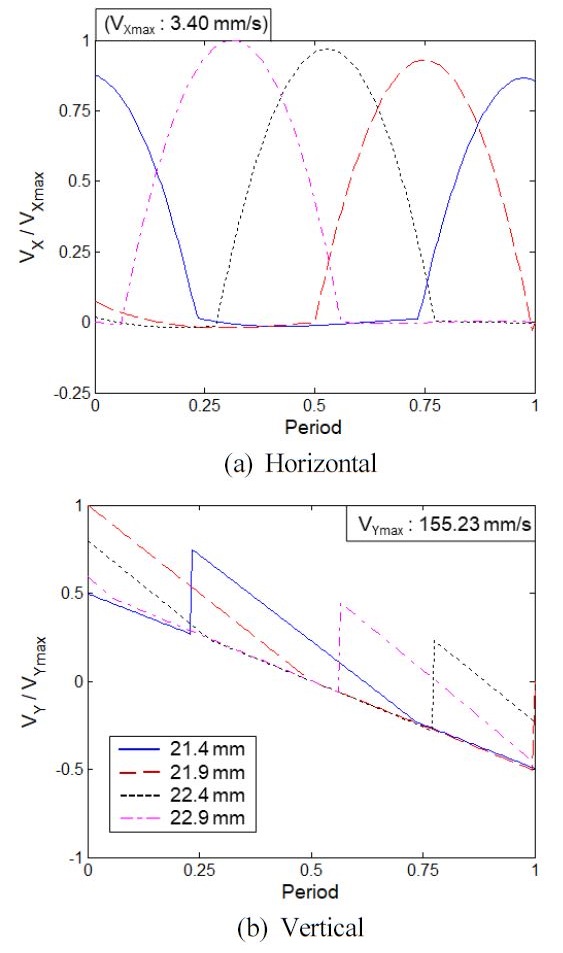
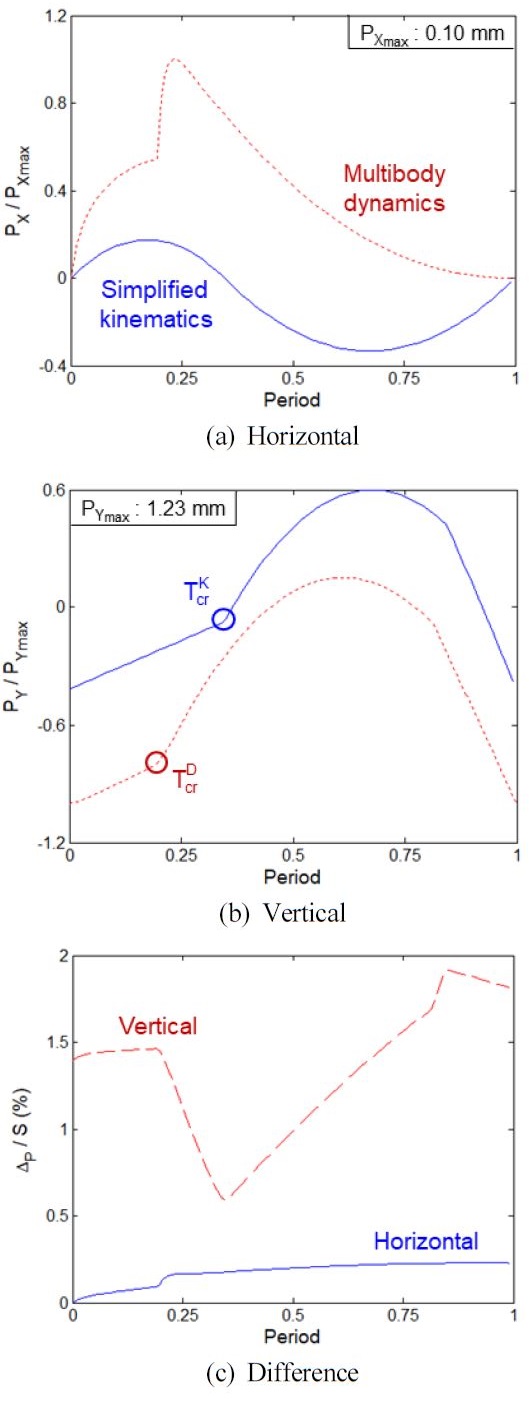
Fig. 6는 한 주기 동안 A의 위치 변동을 수평 및 수직 방향에 대해 무차원화하여 도시한 것이고 Fig. 7은 A의 속도 변동을 동일하게 도시한 것이다.

Fig. 6

Position deviation during one period vs. block length

Fig. 7

Velocity fluctuation during one period vs. block length

그 결과를 보면 블록 길이 L의 변화에 따라 방향에 상관없이 위치와 속도가 크게 영향을 받는 것을 알 수 있다. Fig. 6(a)의 수평 방향 위치의 경우 변동 폭도 최대 0.02mm로 크지 않고 급격한 변화가 없는 반면 Fig. 6(b)의 수직 방향의 경우 최대 변동 폭이 0.86mm로 수평 방향에 비해 상대적으로 크고 두 가지 형태의 급격한 변화도 발생한다. 즉, P^I에서 P^II로 바뀌는 임계 시각 T_cr을 기준으로 크게 변하며 식(8)의 X_OJ가 (-)값에서 (+)값으로 바뀌면서 급격하게 감소함을 알 수 있다.

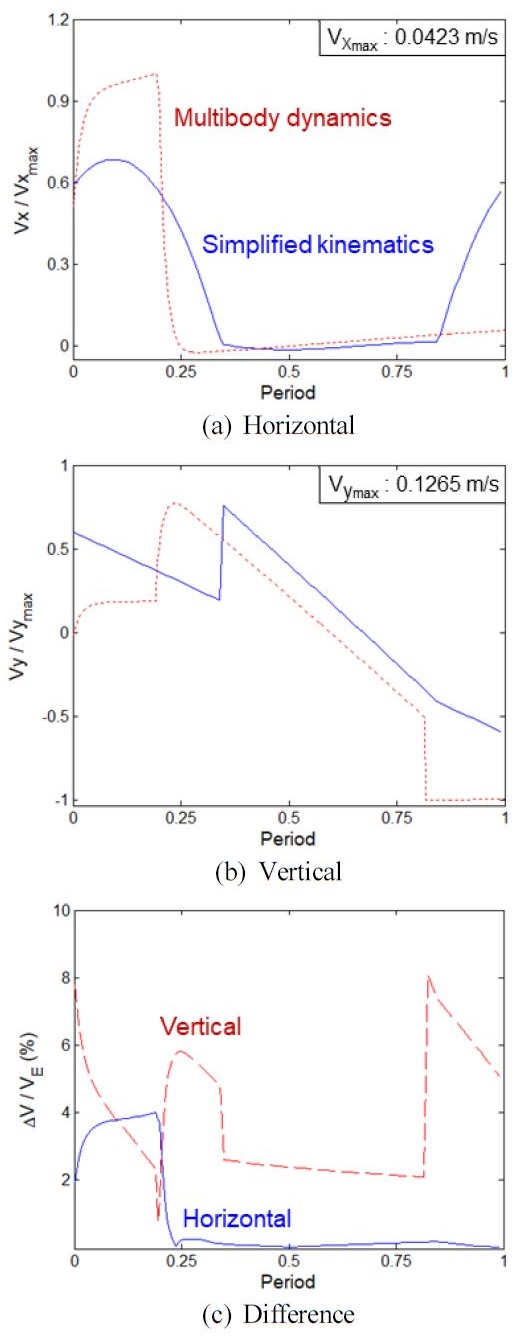
Fig. 7(a)의 수평 방향의 속도 변동을 보면 Fig. 6(a)와 달리 T_cr과 X_OJ의 부호가 바뀌는 시각에서 크게 변하고 Fig. 7(b)의 수직 방향의 경우도 수평 방향과 마찬가지로 T_cr과 X_OJ의 부호에 따라 크게 변하며 변동 폭도 수평 방향과 비교하여 매우 크다.

3.3 다물체동역학 해석을 통한 결과 검증

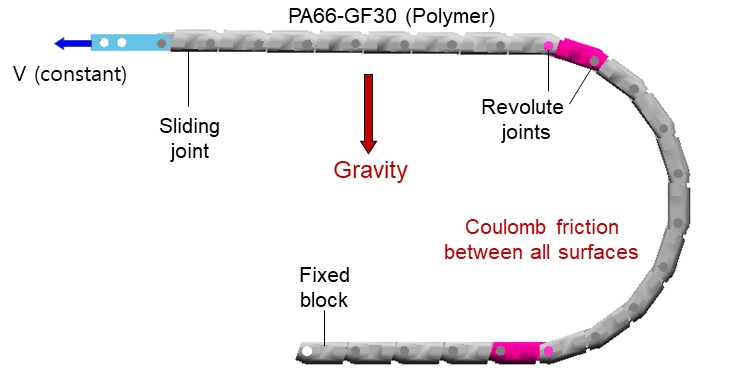
앞 절에서 분석한 체인구동계의 운동 특성은 식(4)의 단순화된 운동학적 방정식으로부터 얻은 결과로서 이를 검증하기 위해 다물체동역학 해석을 수행하였다. Fig. 8은 다물체동역학 코드인 ADAMS를 이용한 다각형 체인구동게의 모델링이며 Table 1은 해석에 적용된 파라미터를 정리한 것이다.

Fig. 8

Multibody dynamics model (ADAMS)

Table 1

System parameters in the ADAMS simulation

Figs. 9과 10은 ADAMS 해석을 통하여 구한 위치 및 속도의 변동특성을 식(4)를 적용한 운동학적 해석 결과와 비교한 것이다. Fig. 9(a)의 수평 위치 변동을 제외하면 한 주기 내의 변동 패턴은 대체적으로 유사하다. 하지만 ADAMS 해석에서는 질량을 고려하기 때문에 임계 시각 $$ T_{cr}^D$$에 도달하는 시간이 운동학적 해석에서 $$ T_{cr}^K$$에 도달하는 시간보다 빠르다. 그 이유는 질량을 고려한 ADAMS 해석에서는 Fig. 1의 직선부 R_S2가 자중에 의한 처짐이 발생하고 그로 인해 Fig. 4(a)의 블록 사이 각 $$ {\delta }_C^I$$의 초기 값이 질량을 고려하지 않은 운동학적 해석보다 작기 때문이다. Fig. 9(b)의 수직 위치 변동에서 ADAMS 결과가 더 작게 나오는 이유도 자중에 의한 처짐의 영향이며 반면에 Fig. 10(b)의 수직 속도 변동의 경우에는 정적 처짐의 영향이 없기 때문에 크기의 차이는 발생하지 않는다.

Fig. 9

Comparison of results in the position

Fig. 10

Comparison of results in the velocity

Fig. 10(a)의 수평 속도 변동의 경우 운동학적 해석에서는 임계 시각에서 급격한 변화가 나타나지 않지만 ADAMS 해석에서는 변동 폭이 크게 증가하는 것을 확인할 수 있는데 그 이유도 질량 효과로 인하여 임계 시각 이후에 P^II 단계로 바뀌면 직선부 R_S2에 속하는 블록 1개가 추가되어 수평 방향의 관성이 커지기 때문이다.

Fig. 9(c)는 ADAMS 해석과 운동학적 해석에서 위치 변동의 차이를 한 주기의 이동거리 2L에 대한 비율로 나타낸 것으로서 수평 방향의 경우 0.23%이고 수직 방향의 경우 1.92%이다. 또한 Fig. 10(c)는 속도 변동의 차이를 끝단 속도 V_E에 대한 비율로 나타낸 것으로서 수평 방향은 3.98%, 수직 방향은 8.08%의 차이를 보인다. 따라서 운동학적 해석을 통하여 구한 체인구동계의 운동 변동 특성은 질량 효과를 무시함으로 인해 오차가 존재하지만 블록 길이가 운동 특성에 미치는 영향을 분석하기 위한 본 연구에서 오차의 영향은 크지 않다.

4. 블록길이가 구동계 운동성능에 미치는 영향

앞 장에서 다각형 블록의 길이 L에 따라 체인 구동계의 위치 및 속도의 변동 폭이 결정된다는 것을 확인하였다. 구동계의 운동 성능은 변동 폭이 작을수록 안정성 및 내구성 관점에서 우수하다고 할 수 있으므로 본 연구에서는 다음과 같이 운동의 성능지수 Q_L을 정의하고 블록 길이를 변화시키면서 Q_L을 구했다.

여기서, D_L은 블록 길이가 L일 때 한 주기 구간에서 위치 또는 속도 변동의 최대값이고 D_max는 L을 15.68mm부터 31.10mm까지 변화시키면서 구한 D_L중에서 최대값이다. 즉 Q_L은 0에서 1 사이에서 변하며 1에 접근할수록 운동 성능이 우수하다.

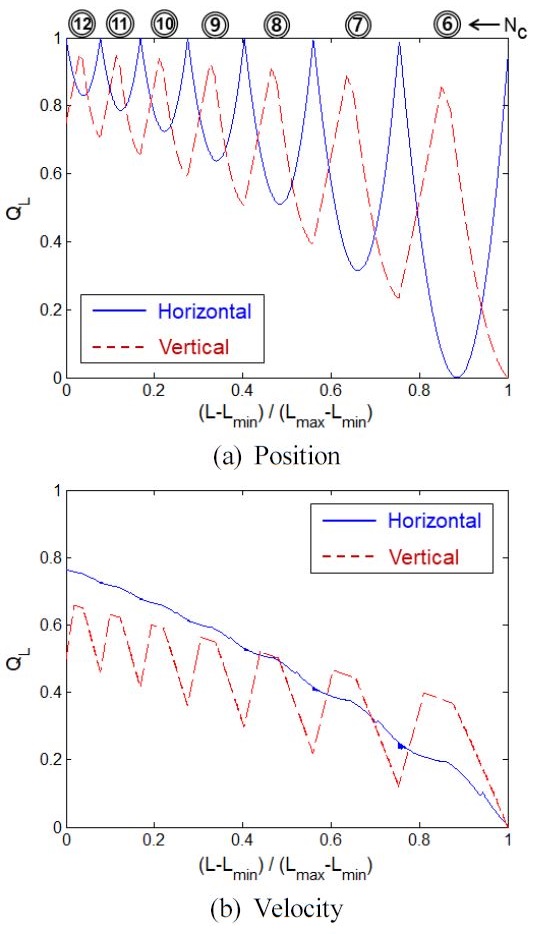
Fig. 11은 그 결과를 도시한 것으로 Fig. 11(a)는 위치에 관한 성능지수이고 Fig. 11(b)는 속도에 관한 성능지수이다. 그 결과를 보면 수평 방향 속도를 제외한 모든 Q_L은 L에 대해 주기적으로 변하는 일정한 패턴을 갖고 있으며 매 주기 마다 Q_L의 최대값과 최소값이 존재한다.

Fig. 11

Performance index vs. block length

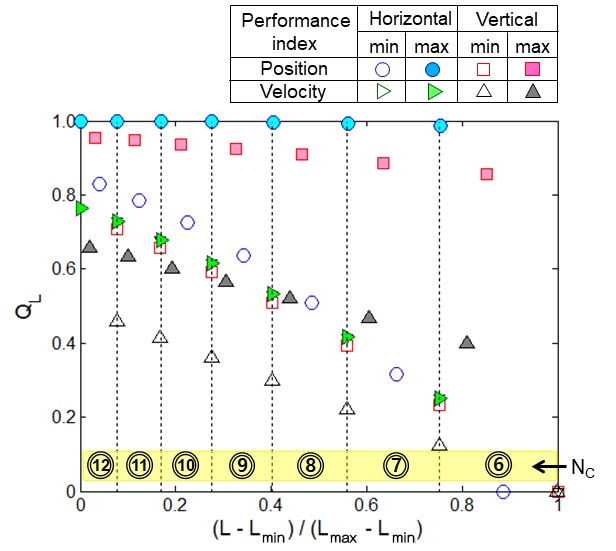
또한 이러한 주기는 Fig. 11(a)에 나타낸 바와 같이 식(4)로 정의되는 변환블록을 제외한 곡선부의 블록 수인 N_C와 밀접한 관련이 있다. Table 2는 N_C가 6에서 12까지 주어질 때 각 N_C에 대한 L의 범위와 Q_L의 최소 및 최대값을 정리한 것이다. N_C가 커질수록 Fig. 11의 모든 Q_L은 1에 접근하게 되는데 이는 블록 길이가 줄어들면서 운동의 변동 폭이 감소하고 구동계의 운동 성능이 좋아진다는 것을 의미한다.

Table 2

Local extremes of the performance indices

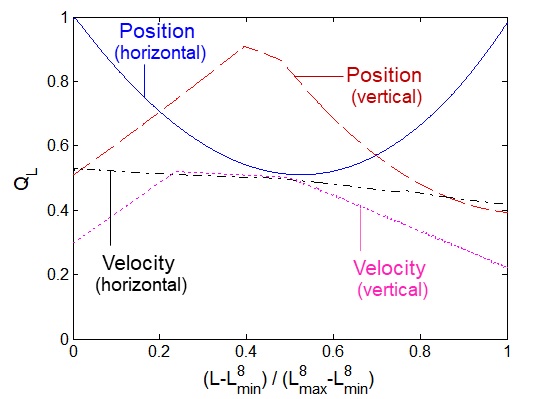
하지만 각 N_C에 대해 국한해서 보면 수평속도의 Q_L만 L의 증가에 따라 감소하고 수직 속도의 Q_L과 수평 및 수직 위치의 Q_L은 L의 증가에 따라 같이 증가하는 경우도 발생한다. Fig. 12는 N_C=8일 때로 한정하여 Q_L과 L의 관계를 확대해서 나타낸 것으로 수평 방향의 위치 및 속도의 경우 L이 최소일 때 Q_L이 최대가 되지만 수직 방향의 경우 L의 증가에 따라 Q_L도 증가하다가 감소하는 경향을 보인다. 또한 수평 방향의 Q_L이 최대가 되는 L에서 수직 방향의 Q_L은 거의 최소가 됨을 알 수 있다.

Fig. 12

Performance index with Nc = 8

Fig. 13은 N_C를 6에서 12까지 변화시키면서 각 N_C에서 Q_L의 최소 및 최대값에 대응하는 L을 표시한 것으로 수평 운동 성능이 가장 좋은 L에서 수직 운동 성능이 가장 좋지 않다는 것을 재확인할 수 있다.

Fig. 13

Extreme values of the performance indices with a variation of the block length

5. 결 론

본 연구에서는 다각형 블록의 체인구동계의 운동 특성을 분석하기 위하여 5절기구로 단순화한 모델을 도출하고 운동학적 해석을 수행하여 구동계의 운동 특성을 구하고 블록길이가 위치 및 속도의 변동에 미치는 영향을 분석하였다.

그 결과를 보면, 곡선부에서 직선부로 변환되는 지점에서의 위치 및 속도는 2단계 주기운동의 형태로 주어지며 단계가 바뀌는 임계시각을 전후하여 급격한 변동이 나타난다. 이러한 변동의 크기는 블록 길이의 영향을 크게 받는데 방향에 상관없이 블록 길이가 작아질수록 운동 변동의 폭은 줄어든다. 또한 구동계의 운동 성능은 곡선부에 속한 블록 수에 따라 주기적 패턴으로 변하는데 수평 방향의 운동 성능이 최적이 되는 블록 길이에서 수직 방향의 운동 성능은 가장 떨어지는 경향을 보인다.

이상의 결과를 종합하면 다각형 블록의 체인 구동계에서 수평 및 수직 방향의 운동 성능을 동시에 우수하게 하는 블록 길이를 결정하는 것은 가능하지 않으며 구동계에 대한 추가적인 고려를 통해서 최적의 길이를 결정할 수 있다. 수평 방향의 속도 변동은 구동계의 동적 불안정을 야기할 수 있으며 수직 방향의 위치 변동은 구동계의 마찰을 증가시킴으로써 내구성 문제를 초래할 수 있다. 따라서 종합적인 관점에서 이러한 고려 사항들의 우선 순위를 분석함으로써 구동계의 성능을 최적화할 수 있는 블록 길이를 정할 수 있다.

References

• Igus, T. C., 2013, Basics of Cable Carriers, Machine Design, 1-4.
• Fuglede, N., Thomsen, J., 2016, Kinematics of roller chain drives, Mechanism and Machine Theory, 100 17-32. [https://doi.org/10.1016/j.mechmachtheory.2016.01.009]
• Pedersen, S. L., Ambroisio, J. A., 2019, A Roller Chain Drive Model Including Contact with Guide-Bars, Multibody System Dynamics, 12:3 285-301. [https://doi.org/10.1023/B:MUBO.0000049131.77305.d8]
• Pereira, C. M., Ambroisio, J. A., Ramalho, A. I., 2010, A methodology for the generation of planar models for multibody chain drives, Multibody System Dynamics, 24 303-324. [https://doi.org/10.1007/s11044-010-9207-x]
• Wang, C. Y., 2016, Vibration of a vertical axially moving string or chain under the influence of gravity, Acta Mech, 228:1 357-362. [https://doi.org/10.1007/s00707-016-1703-5]
• Yang, Z., Li, X., Hong, T., 2015, Transversal Vibration of Chain Ropeway System Having Support Boundary Conditions with Polygonal Action, Shock and Vibration, 2015 1-9. [https://doi.org/10.1155/2015/370248]
• An, C., Su J., 2011, Dynamic Response of Clamped Axially Moving Beams: Integral Transform Solution, Applied Mathematics and Computation, 218:2 249-259. [https://doi.org/10.1016/j.amc.2011.05.035]
• Nguyen, Q. C., Hong, K. S., Ge, S. S., 2011, Transverse Vibration Control of Axially Moving Beams by Regulation of Axial Velocity, 18th IFAC World Congress, 44:1 5579-5584. [https://doi.org/10.3182/20110828-6-IT-1002.03285]
• Sandilo, S. H., Horssen, W. T., 2012, On Boundary Damping for an Axially Moving Tensioned Beam, ASME J. Vibration and Acoustics, 134:1 1-8. [https://doi.org/10.1115/1.4005025]
• Shin, E., Kim, K., 2018, Influence of the Operating Conditions of a Cable Carrier on the Dynamic Characteristics, J of the KSMTE, 27:6 570-576. [https://doi.org/10.7735/ksmte.2018.27.6.570]
• Lee, S. K., Mace, B. R., Brennan, M. J., 2007, Wave Propagation, Reflection and Transmission in Curved Beams, J. Sound and Vibration, 306 636-656. [https://doi.org/10.1016/j.jsv.2007.06.001]