실험계획법을 이용한 냉간 압연기의 채터링 분석
Abstract
Cold rolling can be described as a processing method that is often used for materials with a small thickness or cross-section, or for finishing work to obtain products with accurate dimensions and clean surfaces. However, as the speed of this process increases to improve productivity, chatter vibration occurs due to the imbalance and eccentricity of the rolling roll, damaging the gear drive unit and the bearing. Therefore, in this study, to analyze the main cause of chatter vibration in the cold rolling system, chatter vibration phenomena according to various rolling conditions were calculated using a multi-body dynamics model. In addition, the experimental design method was used to statistically analyze the calculated data and the interaction effects that could correlate with the main factors causing chatter vibration were investigated. Finally, a simple regression equation model is presented.
Keywords:
Chattering, MBD (Multi-body dynamics), Cold rolling mill, DOE (Design of experiment), Regression equation1. 서 론
냉간압연 공정은 열간 압연제품을 소재로 하여 수요자가 원하는 치수로 최종 압연을 하는 공정이다. 최근 더욱더 정밀한 품질의 압연제품의 요구로 인하여 압연 진동에 있어 채터 진동에 대하여 활발한 연구가 진행되고 있다. 이러한 채터 진동은 평판에 굴곡을 만들어 제품의 질을 저하시키는 주요 원인으로 분석되고 있다. 주요 원인으로 압연롤의 불균형과 편심, 기계 조립 부위의 이완, 미스얼라인먼트, 롤슬립, 기어 구동부 및 베어링 손상등 기계적 요인들을 생각할 수 있다[1-3]. 하지만, 이러한 채터 진동의 메카니즘은 매우 복잡하고 어려워 해결 방법을 찾는 일이 쉽지만은 않은 실정이다[4,5]. 이를 해결하기 위하여 압연기의 토크와 진동주파수를 측정[6]하였고, 압연 파라미터의 영향을 분석하기 위하여 유한요소법을 이용하여 채터진동을 분석하였다[7]. 또한 유도전동기의 슬라이드 모드를 수학적 모델링과 실험을 통하여 분석[8]하였고, 유한요소법을 이용하여 6단 압연기의 후판공정에서의 판 예측을 통한 분석이 진행되었다. 하지만 일부 시스템의 원인 분석에는 전체 시스템의 복합적 원인을 분석하기에는 한계가 있다. 따라서 개략적인 냉간 압연시스템을 모델링을 하고 이를 실험 데이터와의 검증 후 주요 원인을 분석 할 필요가 있다.
따라서, 본 연구에서는 1/2 냉간압연 시스템의 개략적인 모델링을 구축하였고 MBD (Multi Body Dynamics)방법을 이용하여 가상 데이터를 취득하여 기존의 실험 데이터와 비교 분석하였다. 취득한 데이터의 주요 원인을 분석하는데 있어 실험계획법(Design of Experiment; DOE)이 주로 사용되고 있다. 실험계획법은 공정의 특성에 영향을 미치는 주요 인자들을 선정하고 이들 간의 관계를 체계적으로 설정하기 위한 실험을 실시하고 그 결과를 분석함으로써 주효과와 인자들의 교호작용 모두를 고려 할 수 있다. 일반적으로 냉간 압연 시스템과 같이 복잡한 시스템에는 교호작용이 존재한다. 예를 들어 구동 장치인 헬리컬기어에서 발생한 가진력과 스트립에 작용되는 압하력과 상호간에 영향 혹은 각 롤러간의 마찰로 인한 영향들을 고려한다면 효과적인 원인 분석을 할 수 있을 것이다.
본 연구에서는 압연 공정에서 가진력이 발생되는 구동기어의 회전속도와 이를 전달하는 스핀들의 강도 그리고 롤러 간의 마찰강도 그리고 스트립을 누르는 하중 등을 채터링 주파수 발생의 주요 파라미터로 선정하고 각 파라미터 값에 대한 Full factorial 비반복 실험을 하였다. 또한 Pooling 작업을 통하여 반응인자에 대한 회귀식을 도출하였다.
2. 다물체 동역학 해석
Chatter 진동을 특성하는데 있어 실제로 많은 실험을 통해 분석하기 위해서 많은 한계가 있다. 따라서, 실험의 압연시스템과 근사화된 시뮬레이션 모델링을 하고 일부 실험데이터와 근사화된 시뮬레이션 데이터를 비교 검증할 필요가 있다[9-10].
2.1 다물체 동역학 모델
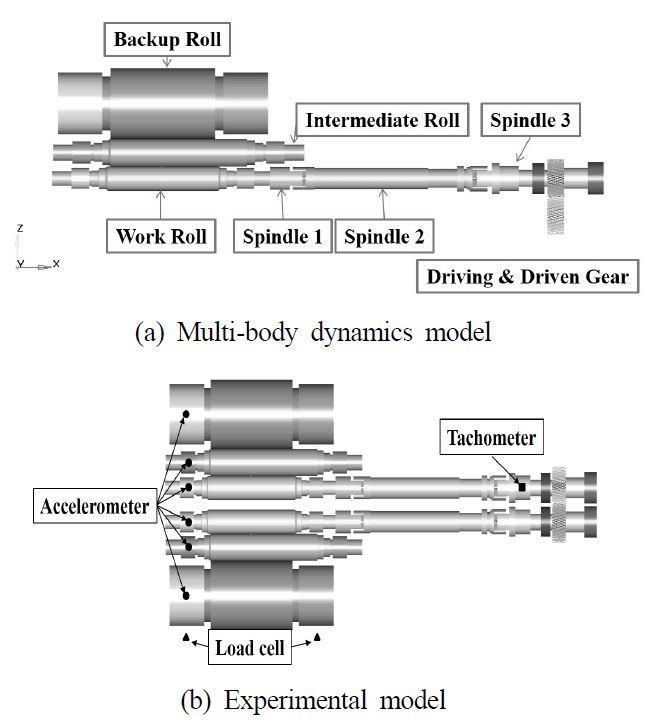
냉간압연 시스템의 구조는 크게 Fig. 1(a)와 같이 나눌 수 있다. 압연기에 힘을 발생시키는 구동 기어와 피동기어, 기어로부터 발생된 토크를 작업 롤에 전달시키기 위한 스핀들 그리고 두꺼운 재질의 스트립을 압연하는 작업롤러와 스트립의 형상을 컨트롤 하는 중간롤러, 롤러들의 굽힘을 억제 시키는 백업 롤러로 구성되어있다.
2.2 실험 및 다물체 동역학 해석
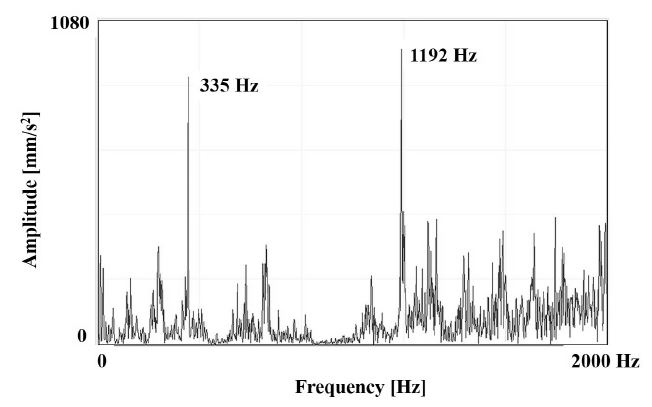
압연기로부터 발생하는 채터 진동을 측정하기 위하여 스트립에 가장 직접적인 영향을 미치는 작업롤의 진동을 측정하였다. 가속도 센서를 작업롤 초크에 부착하여 진동 가속도를 Fig. 1(b)와 같이 측정하였다. 또한 타코미터를 이용하여 스핀들의 회전속도를 측정하였으며, 로드셀을 이용하여 압연하중을 측정 하였다[11-12]. Fig. 2는 작업 롤러의 수직가속도에 대하여 FFT (Fast Fourier Transform)변환을 한 실험 결과이다. 여기서, 355 Hz는 기어에 대한 메쉬 주파수로, 식 (1)을 통하여, 이론적으로도 계산될 수 있다.
| (1) |
이 주파수를 통하여 기어에서 발생한 기어 메쉬 주파수가 스핀들을 통하여 작업 롤까지 전달되고 있음을 알 수 있다. 만일, 스트립에 주기적인 간격으로 채터 마크가 발생한다면, 식 (2)와 같이 채터 주파수를 계산할 수 있다.
| (2) |
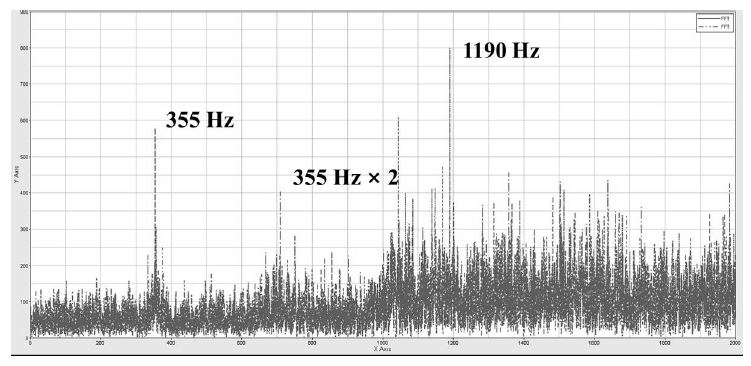
실험에서의 주파수는 1192 Hz로 이론을 통해 계산된 주파수의 값과 일치한다. 이론 데이터와 실험 데이터는 Fig. 3인 MBD 해석결과를 통하여 비교 검토가 가능하다. 기어 메쉬 주파수는 355 Hz인 구동 주차수와 710 Hz가 계산되어 실험에서의 데이터와 동일한 주파수가 계산되었다. 작업 롤에 대한 수직 주파수는 1190 Hz가 계산되어 실험에서의 1192 Hz와 미소한 차이가 계산되었다. 하지만 이는 주파수 허용범위 내에 포함이 되고 주파수 발생의 형태가 실험과 유사한 형태로 발생함으로써 시뮬레이션 결과가 시험과 유사한 결과를 나타냄을 알 수 있다. 따라서 MBD 결과 데이터를 이용하여 채터링 주파수 원인 분석이 가능하다고 할 수 있다[13].
3. 실험계획법
실험계획법은 공정의 특성에 영향을 주는 인자들을 선정하고 조작하여 인자간의 관계를 체계적으로 조사하기 위하여 실험을 실시하여 데이터를 얻고 이를 분석함으로써 주요한 원인을 찾아내고자 하는 방법이다. 이는 품질에 대한 신뢰성과 생산성 및 가격 절감에 기여하고 있다. 이러한 실험계획법은 크게 완전요인(full factorial)법과 일부요인(fractional factorial)법으로 구분할 수 있다. 완전요인 법은 모든 주효과 및 인자들 간에 교호작용을 고려할 수 있는 장점이 있으나 요소의 수에 따라 실험횟수가 급격하게 증가하고 잡음인자가 포함 할 수도 있다. 인자의 수를 k, 실험 수준을 n, 반복 횟수를 m이라고 하면 이는 다음 식과 같다.
| (3) |
반면에 일부요인 실시법은 완전 요인실험에서 잡음인자와 영향력이 적은 인자를 제외한 일부를 실행하여 주요 요인을 선별하는 방법으로 고차원의 교호작용 효과는 무시할 수 있을 정도로 희박하다는 ‘효과와 희박성의 원리(The sparsity of effects principle)’에 의하여 주효과와 낮은 차수의 교호작용만을 고려하는 방법이다. 이 때 일부를 제외한 실험횟수를 q라고 할 때 다음과 같이 감소한다.
| (4) |
실험계획법에 의하여 실시된 결과들은 각각 인자들에 대한 주효과와 2차의 교호작용 효과를 비교해 주어야 한다. j번째 인자의 주효과와 k번째의 인자간의 교호작용은 다음식과 같다.
| (5) |
| (6) |
| (7) |
여기서, Ri는 i번째 실험에 대한 결과치를 말하며, Ej는 j번째 요인에 대한 주효과를 나타낸다. ljk는 j번째 인자의 수준을 -1과 1사이에 정규화 시킨 값으로 다음과 같이 직교성을 만족한다.
3.1 3수준 주요 인자 선정
본 연구에서는 냉간압연 시스템의 압연공정에서 발생하는 채터 주파수를 발생시키는 주요 인자를 실험계획법을 통하여 도출하였다. 채터 마크를 방지하기 위해서는 채터 주파수를 발생시키는 주요 원인을 찾는 것이 중요하다. 따라서, 냉간 압연시스템의 다양한 파라미터를 설정하고 이를 조작하여 채터링 주파수를 발생시키는 주요 원인을 찾을 필요가 있다. 채터 마크 현상은 스트립에 나타난다. 스트립에 영향을 주는 요인으로 작업롤러의 강도와 작업롤러와 스트립간의 마찰강도 그리고 작업롤러가 스트립에 가하는 압하력이 중요할 것이다. 또한 압연기를 구동시키는 역할을 하는 기어의 속도와 이를 전달하는 스핀들의 강도에 따라 가진력에 의한 채터 마크 현상이 발생 할 수도 있다. 각 파라미터의 초기 실험의 데이터와 비교 분석하기 위해 Table 1과 같이 5가지의 주요인자 와 초기 실험데이터의 상・하 값인 3 수준에 대한 값들을 적용하였다. 냉간 압연 시스템에서 채터링 주파수 발생요인으로 선정된 주요 인자에 대하여 Full factorial 실험결과 총 243회의 비반복 실험을 하였고 Table 2와 같이 각 파라미터의 가속도 값에 대하여 FFT 변환을 하였고 Table 3과 같이 결과를 확인 하였다. 5요소에 대한 3수준 실험결과는 비반복 실험이기 때문에 각 파라미터에 대한 유의수준에 대한 만족 여부를 판단하는 데는 한계가 있다.
3.2 2수준 요인 선정 및 실험 분석
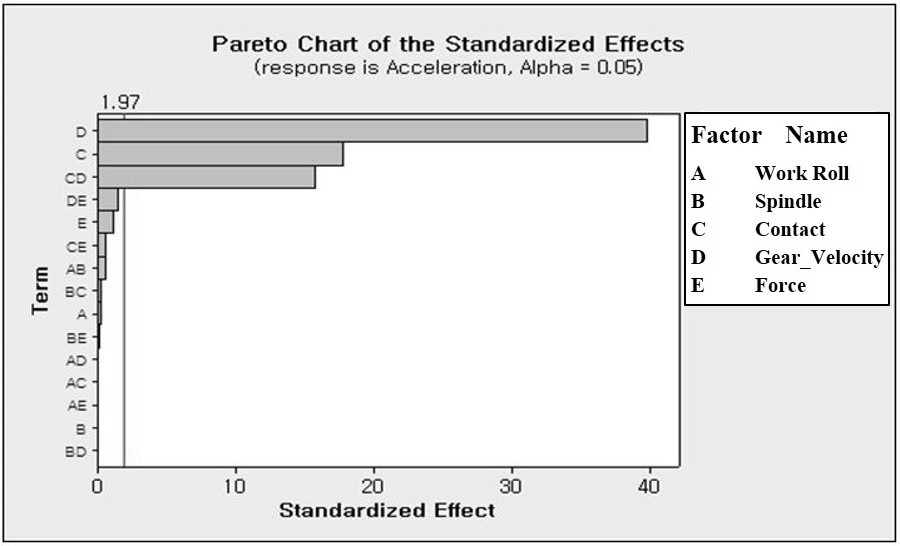
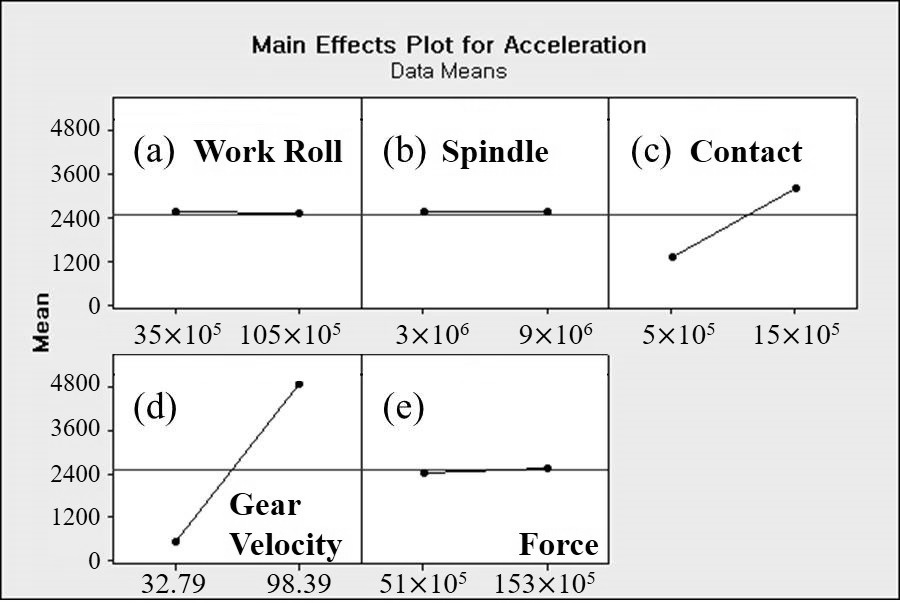
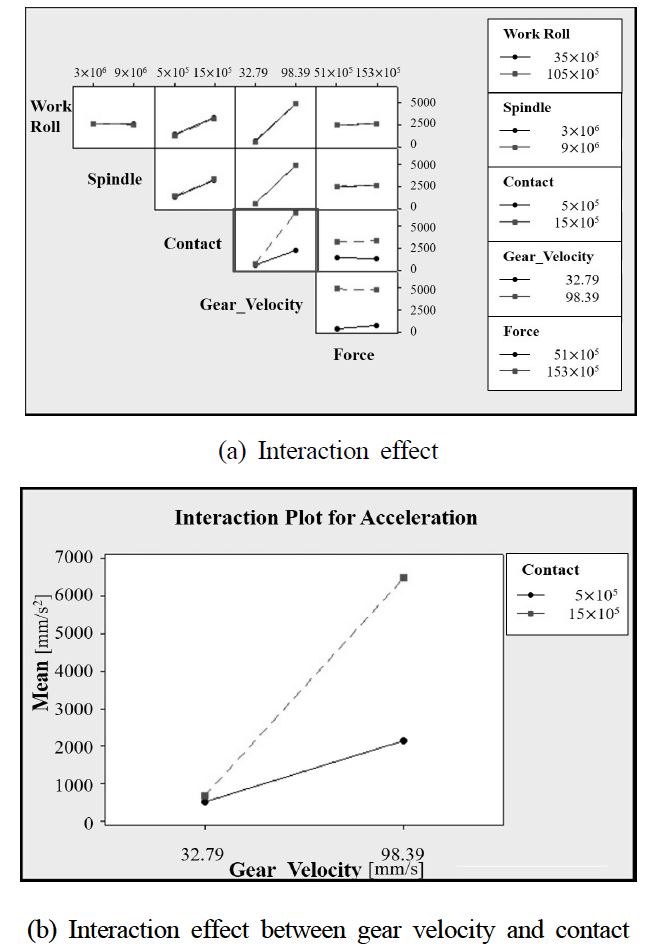
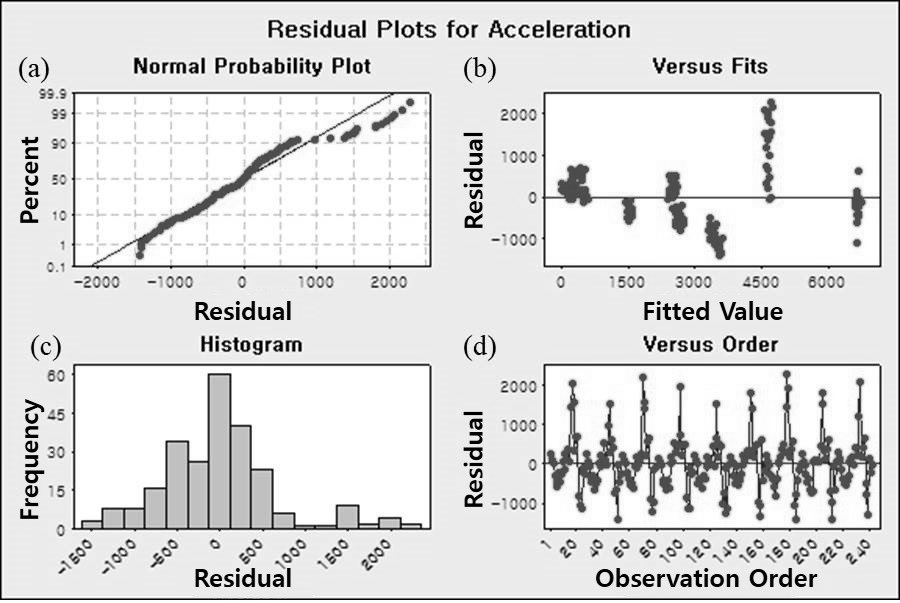
3수준데이터를 2수준 데이터로 변환하기 위하여 Table 4와 같이 기존의 상, 하한 값을 결정하고 나머지 값에 대해서 center point로 설정하였다. 또한, 일반적으로 인자수가 많을 경우 고차교호작용의 영향력은 극히 적으므로 유의하지 않다고 할 수 있다. 따라서, 3차 이상의 교호작용에 대하여 Pooling 작업하였다. 앞선 실험계획 방법과 마찬가지로 2수준의 요인에 대한 해석 결과 Fig. 4를 통하여 유의한 인자를 판별 할 수 있었다. 또한, Fig. 5를 통하여 유의 정도에 대한 크기를 가늠해 볼 수 있다. 2수준 Full factorial 실험결과 가진력 발생에 직접적으로 영향을 주는 기어의 속도와 작업롤러와 스트립간의 마찰강도가 채터링 주파수 발생에 영향을 준다는 것을 예상 할 수 있다. 그리고 이 두 요인 사이에서는 교호 작용 계산 결과를 통해 상관계가 발생 할 수 있다는 것을 알 수 있다. 채터링 주파수 발생에 영향을 알아보기 위하여 우선 각 요소에 대한 개별적 효과를 Fig. 6으로 확인하였다. Fig. 6(a)는 작업롤러 강도에 의한 효과이고 강도가 증가함에 따라 0.03 m/s2의 진동 가속도가 작아지는 것을 알 수 있다. Fig. 6(b)는 스핀들 강도에 의한 효과이고 강도가 증가함에 따라 0.004 m/s2의 진동 가속도가 증가하는 것을 알 수 있다. Fig. 6(c)는 작업롤러와 중간롤러 사이의 접촉 강도에 의한 효과이고 강도가 증가함에 따라 1.93 m/s2의 진동 가속도가 증가하는 것을 알 수 있다. Fig. 6(d)는 기어 속도에 의한 효과이고 강도가 증가함에 따라 4.33 m/s2의 진동 가속도가 증가하는 것을 알 수 있다. Fig. 6(e)는 작업에 가해지는 압하중에 의한 효과 이고 강도가 증가함에 따라 0.12 m/s2의 진동 가속도가 증가하는 것을 알 수 있다. 따라서, 작업롤러의 강도와 스핀들의 강도 그리고 작업 롤에 가해지는 압하중은 채터링 주파수 발생에 아주 미소하게는 영향을 주지만 기어의 회전속도와 중간 롤과 작업 롤의 접촉강도에 비해 매우 미소하게 영향을 미침을 알 수 있다. 특히 가진력에 직접적으로 영향을 주는 기어의 회전 속도가 채터링 주파수 발생에 가장 큰 영향을 미치고 롤의 접촉강도 역시 무시 할 수 없을 정도로 큰 영향을 미침을 알 수 있다. 하지만 이는 각각의 효과만을 의미한다. 따라서, 각 효과가 복합적으로 작용(교호작용) 하였을 경우를 추가적으로 확인 할 필요가 있다. Fig. 7은 채터링 가속도에 대하여 2차 교호작용에 대한 효과도를 의미한다. 일반적으로 교호작용 효과에 대한 분석은 각각의 그래프의 기울기에 대한 평행선 여부를 보고 판단하거나 95%의 신뢰 구간을 기준으로 P-value의 값이 0.05보다 작은 값인지를 확인함으로써 유의성 여부를 결정지을 수 있다. 따라서, Fig. 7의 확대도와 Table 5의 P-vale 값을 통해 롤 사이의 접촉 강도와 기어의 회전 속도가 낮을수록 이 두 요인 사이의 연관성을 확인할 수 있다. 하지만, 이러한 데이터는 비반복 실험에 대한 결과이기 때문에 정규성을 띄고 있는지 그리고 랜덤화가 이루어진 데이터 인지를 확인 할 필요가 있다. 따라서, Fig. 8과 같이 잔차 도표를 통하여 통계적으로 유효한지 여부를 확인하였다. 대부분의 잔차는 Fig. 8(a)와 같이 정규회귀선과 유사한 형태를 띄고 있고, Fig. 8(b)를 통해 자찬들이 상, 하 대칭이고 0값의 주위에 랜덤하게 분포되어있기 때문에 회귀모형이 적절하다고 할 수 있다.
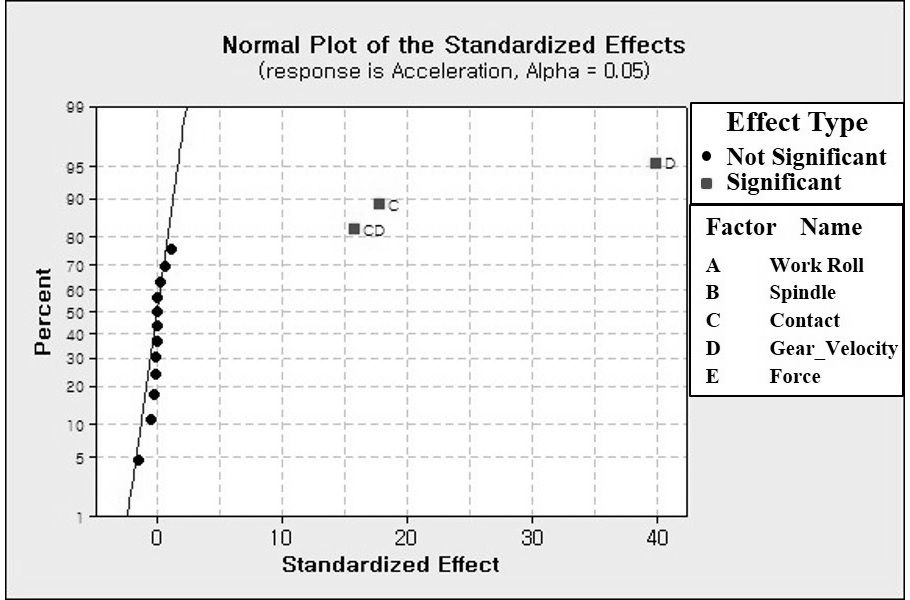
Normal probability distribution of the standardized effect of FFT transformed chattering acceleration
잔차값들에 대한 히스토그램 역시 Fig. 8(c)와 같이 정규분포와 유사한 형태로 분포가 되어있음을 확인하였다. 또한 예측값의 변화와 시간에 따른 잔차의 패턴 검사를 통하여 Fig. 8(d)와 같이 일정한 형태의 데이터가 아닌 랜덤화된 데이터임을 확인하였다.
마지막으로, 채터링 진동에 미치는 영향도를 간단히 확인할 수 있는 회귀모델 식을 제안하고자 한다. 제안된 모델은 각각의 요소와 요소들 사이의 반응치 계산 결과인 Table 5로부터 다음과 같이 구성될 수 있다.
| (8) |
여기서, A는 작업롤의 강도(WR)이고 B는 스핀들의 강도(SP), C는 작업롤러와 스트립간의 마찰강도(CON), D는 기어의 속도(Vel) 그리고 E는 작업 롤에 작용하는 압하중(F)으로 각 요소를 의미한다.
회귀모델에 대한 검증은 실험계획법의 수행 결과에 대한 정확도로부터 판단할 수 있다. 본 연구에서 제안하는 회귀 모델은 실험계획법의 정확도인 90.45%로 일반적으로 허용 기준치인 80%보다 높기 때문에 활용 가능한 모델이라고 할 수 있다.
4. 결 론
본 연구에서는 냉간 압연 시스템의 채터링 현상을 발생시키는 주요 및 교호작용 효과를 이용한 원인 분석을 위하여 다물체 동역학(MBD)방법과 실험계획법을 이용하였다. 다물체 동역학 모델은 조업과정에서 측정된 실험데이터와 비교하여 검증하였다. 또한 해석 결과로부터 채터 마크의 주요 원인은 기어의 진동 주파수로부터 발생되는 것을 확인하였다.
제품의 품질을 저하시키는 채터링 진동 현상을 예방하기 위해 구조적 요인인 작업롤러와 스핀들의 강도, 압연 조건인 작업롤러와 스트립 사이의 접촉 강도와 기어의 회전 속도 그리고 작업롤에 가해지는 압하중을 주요 원인으로 선정하였고 실험계획법을 이용하여 주요 원인 및 교호작용을 확인하였다. 그 결과, 채터링 주파수는 냉간 압연 시스템의 구동 장치인 구동 헬리컬 기어의 회전속도와 작업롤러와 스트립사이의 접촉강도에 따라 크게 영향을 받는다는 것을 확인 할 수 있다. 특히 기어의 고속회전 시 급격한 채터링 진동을 발생시킬 수 있고 저속 회전 시에는 스트립과의 마찰관계를 고려해야하기 때문에 추후 생산 속도를 고려한 최적의 기어속도를 확인할 필요가 있다. 마지막으로 제시된 변수들을 기준으로 채터링 진동 특성을 쉽게 파악할 수 있는 회귀 방정식 모델을 제시함으로써 냉간 압연기의 설계 및 압연 구동 조건의 선정에 간단한 활용 도구로 사용될 수 있을 것이다.
Nomenclature
| wG : | Gear mesh frequency [Hz] |
| z : | Number of toothed wheel |
| w : | Rotational velocity of gear [rpm] |
| fchatter : | Chatter frequency [Hz] |
| Vl : | Feed rate of strip [m/min] |
| Pc : | Chatter mark pitch spacing [mm] |
| k : | Factor number |
| n : | Experiment level of the analysis model |
| m : | Repeated number of the analysis model |
| q : | Number of the analysis model |
| Ri : | ith analysis results of the model |
| Ei : | Main effect results |
| ljk : | Normalized value between –1 and 1 to the level of jth factor |
References
- Byon, S. M., Lee, S. M., Jun, E. C., 2011, Numerical and Experimental Prediction of Asymmetric Deformation Behavior and Its Setup Model in Plate Rolling, Journal of Korean Society of Manufacturing Process Engineers, 10:2 124-129.
-
Aistleitner, K., Mattersdorfer, L. G., Haas, W., Kugi, A., 1996, Neural Network for Identification of Roll Eccentricity in Rolling Mills, Journal of Materials Processing Technology, 60:1 387-392.
[https://doi.org/10.1016/0924-0136(96)02359-X]

-
Edwards, W. J., 1978, Design of Entry Strip Thickness Controls for Tandem Cold Mills, Automatica, 14:5 429-441.
[https://doi.org/10.1016/0005-1098(78)90002-X]

- Lee, C., 1999, The Study on Chatter Mechanism and Friction Induced Self-Excited Vibration in The Rolling System, Master’s thesis.
- Jun, H., Lee, J., Lee, S., 1995, Chatter Vibration in Hot Strip Finishing Mills, Trans. of the KSME (A), 35:5 414-426.
- Son, B., Roh, Y., Lee, Y., 1994, The Cause of Vibration at Finishing Stands in a Hot Strip Mill, Korean Society for Noise and Vibration Engineering, 4:1 43-50.
- Mehrabi, R., Silani, M., Ziaei-Rad, S., Salimi, M., Kamranian, A., 2008, Investigation of Influences of Operational Parameters on Chatter Vibration of Cold Rolling Machines Using Finite Element Method, Steel Research International, 1 467-474.
-
Seo, S. J., Kim, D. W., Park, G. T., 2004, Design of Adaptive Fuzzy Sliding Mode Controller for Chattering Reduction, Journal of Korean Institute of Intelligent System, 14:6 752-758.
[https://doi.org/10.5391/JKIIS.2004.14.6.752]

- Bingsheng, W., Niu, P., 2015, Analysis and Simulation of Work Rolls in Cold Rolling Mill Based on Adams, Forging & Stamping Technology, 11 38.
- Hyperworks, 2009, Motion View Introduction, HyperWorks 9.0 Release, Altair Engineering Inc 86.
- Kang, K. W., Kim, B. T., 2009, Study on Diagnostic Analysis of Mill Chattering in Tandem Cold Mill Stand, Proceedings of the Korean Society of Precision Engineering Conference, 471-472.
-
Niroomand, M. R., Mohammad R. F., Heidari, A., 2019, Experimental Analysis of Vibration and Sound in Order to Investigate Chatter Phenomenon in Cold Strip Rolling, The International Journal of Advanced Manufacturing Technology, 100:1-4 673-682.
[https://doi.org/10.1007/s00170-018-2639-9]

-
Kim, Y., Park, H., Lee, S., Kim, C., 2012, Experimental and Numerical Investigation of The Vibration Characteristics in a Cold Rolling Mill Using Multibody Dynamics, ISIJ International, 52:11 2042-2047.
[https://doi.org/10.2355/isijinternational.52.2042]