직사각형 덕트 층류유동에 대한 종횡비 효과 수치해석 연구

1. 서 론

덕트 유동은 공학에서 다양하게 응용되고 있으며, 열 및 물질 전달, 연료전지, 냉각장치 및 열교환기 등 많은 부분에서 활용되고 있다. 이런 이유로 많은 연구자들이 덕트 내 유동 마찰계수와 열전달 관점에서 많은 연구들을 수행하여왔다^[1-3]. 예를 들어 Ma et al.^[4]은 직사각형 수로 내 등온 및 비등온 조건에서 Reynolds 수가 변할 때 층류유동과 난류유동에서의 마찰계수 및 열전달에 대한 실험 연구를 수행하였다. Wang et al.^[5]도 유사하게 직사각형 수로의 단상유동 실험에서 벽 온도, 열유속, 입출구 온도 및 압력 강하로부터 마찰계수와 Nusselt 수의 상관관계를 확인하였다.

그러나 이 논문들은 종횡비가 0.05로 고정된 경우만을 고려하였다. 최근 Xing et al.^[6] 연구에 따르면 직사각형 덕트 내 완전발달된 층류유동에 대해 종횡비의 영향에 따라 평균 마찰 계수 등이 상당히 바뀌게 된다는 사실이 보고된 바 있다. 이와 같이 덕트 내 층류유동에 대하여 실험 및 이론을 통한 연구가 상당수 존재하나, 종횡비에 따라 덕트 내 층류유동 특성을 아직 완벽히 이해한다고 할 수 없다. 따라서 본 연구에서는 종횡비에 따른 층류유동 특성을 살펴보고자 한다. 특히 본 연구에서는 Papautsky et al.^[3]가 지적한 바와 같이 표면처리^[7] 또는 입출구 영향으로 인해 실험적으로 연구하기 힘든 입구길이에 대한 내용도 살펴보기 위해 수치해석적인 방식을 사용하였다. 예를 들어 Vinuesa et al.^[8]에서는 난류 경우에 대해 수치해석적인 방식으로 입구길이에 대한 연구를 수행한 바 있다.

2. 수치해석 방법

본 연구에서는 종횡비에 따른 덕트 내 층류유동 특성을 수치해석을 이용하여 연구하였으며, 모든 종횡비에 대하여 Reynolds 수(Re=VD_h/v, V는 평균속도, D_h는 수력직경, v는 동점성계수)는 1000으로 고정하였다. 해당 Reynolds 수는 기존 문헌에 따르면 모든 종횡비에 대하여 층류유동에 해당한다.

층류 덕트 유동에 대해 Reynolds 수 외에 종횡비는 중요한 인자 중 하나로 고려되어야 한다. 본 연구에서 종횡비는 덕트의 넓은 면(a)에 대한 좁은 면(b)의 비율로 정의된다. Table 1에서와 같이 본 연구에서 고려한 종횡비(AR)는 0.05~1이다.

Table 1

Mesh size with respect to the aspect ratio of the duct

참고로 Bhuhan and Singh^[9]에 따르면 solar air heater에 사용하는 공기 덕트의 종횡비는 0.0869~0.147의 범위를 가진다. Sahu and Bhagoria^[10]에서는 종횡비가 0.125이다. 그리고 Yuan et al.^[11]에 따르면 연료 전지에 사용하는 덕트 종횡비는 0.2~1의 범위를 가진다.

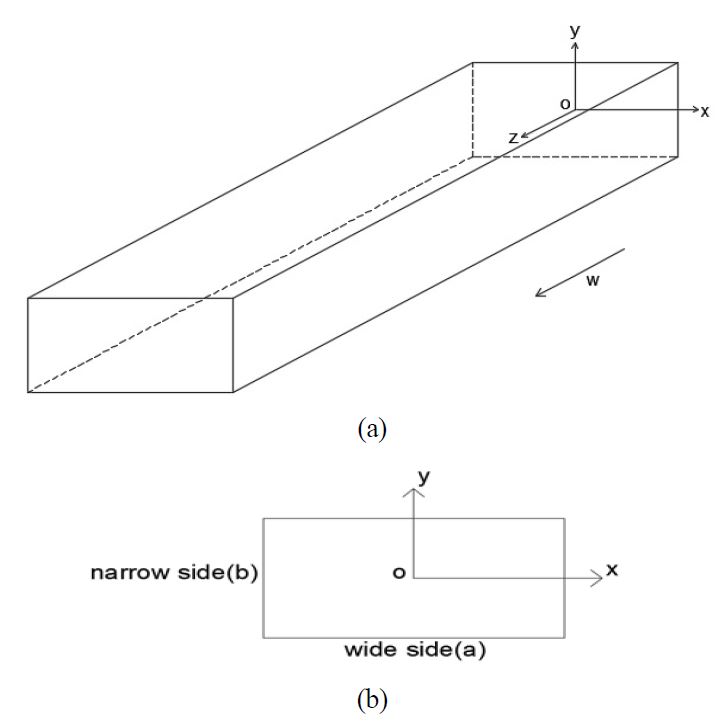
Table 2는 층류 덕트 유동에 대한 최근 연구 조건을 정리해서 보여준다. Table 2에서와 같이 최근 종횡비 0.05와 같이 종횡비가 작은 경우에 관심을 가지고 연구가 진행되고 있으며, 따라서 본 연구에서도 0.05를 가장 작은 종횡비로 하여 연구를 수행하였다. Fig. 1(a)와 1(b)는 종횡비가 b/a인 직사각형 덕트 형상을 보여준다.

Table 2

Reference paper data

Fig. 1

Schematic of the rectangular duct: (a) computational domain; (b) Cross section plane

본 연구에서는 서론에서 서술한 바와 같이 완전발달영역뿐만 아니라 발달영역 유동 분석을 위해서 수치해석을 수행하기 위해 ANSYS Fluent를 사용하였다. 본 연구 영역이 층류임을 고려하여 정상상태 계산을 수행하였다. 입구 경계 조건은 각 종횡비 수력직경 기준 Re=1000이 되는 속도를 균일하게 부가하였으며, 출구경계조건은 일정압력조건을 고려하였다. 공간차분법으로는 압력과 운동량에 대해 2차 정확도를 고려했다. 반복법 계산 기준은 10^-9로 하였다. 각 종횡비에 따른 계산영역과 격자 정보는 Table 1에 주어진다. 격자 구성은 균일격자를 고려하였으며, Table 1에서 볼 수 있는 바와 같이 단면격자수는 단면 내 속도분포를 예측을 위하여 80×80개를 고려하였다.

3. 수치해석 결과

Table 3은 종횡비에 따른 입구 길이(L)를 보여준다. 덕트 내 유동 입구 길이는 Muzychka and Yovanovich^[12]에서는 scaling analysis라는 이론적인 방법을 통해 연구하는 등 관심을 가지는 내용이다. 본 연구에서는 입구길이는 중심점에서의 축방향 속도가 출구에서의 값과 비교하여 0.99배에 해당하는 위치로 정의하였다. Table 3에서 볼 수 있듯이 종횡비가 감소함에 따라 수력직경 대비 입구길이(L/D_h)는 감소하게 된다. 참고로 매끈한 파이프에 대한 입구길이는 약 60이며, 이 값은 종횡비가 1일 때 값과 유사하다.

Table 3

Duct entrance length with respect to the aspect ratio of the duct

최근 덕트 유동 입구길이에 대한 연구를 수행한 Vinuesa et al.^[8]은 입구길이를 좁은 면 길이로 무차원화해서 나타낸 바 있으며, 이에 따라 본 연구에서 얻은 입구길이를 좁은 면 길이로 무차원화해서 나타내면 Table 3과 같다. Table 3에서 볼 수 있듯이 수력직경으로 무차원화한 경우와 비교하여 좁은 면 길이로 무차원화한 경우 입구길이는 증가하여 O(10~100) 근처의 값을 가지게 된다.

Fig. 2는 종횡비 변화에 따른 덕트 중심점 축방향 속도(w_c/w_b)를 보여준다. Fig. 2에서 축방향 속도는 입구에서의 균일 속도(또는 bulk 속도)로 무차원화 하였다. Fig. 2에서 볼 수 있듯이 층류 덕트 유동에서 종횡비가 감소함에 따라 bulk 속도 대비 중심속도는 점차 감소하며, 본 연구에서 고려한 최소 종횡비 0.05에서는 약 1.5 근처의 값을 가진다. 1.5는 무한 평판 채널에서 bulk 속도 대비 중심 속도의 값이다. 따라서 종횡비가 0.05 근처에서 덕트 유동은 무한 평판 채널 유동에 근접하게 된다.

Fig. 2

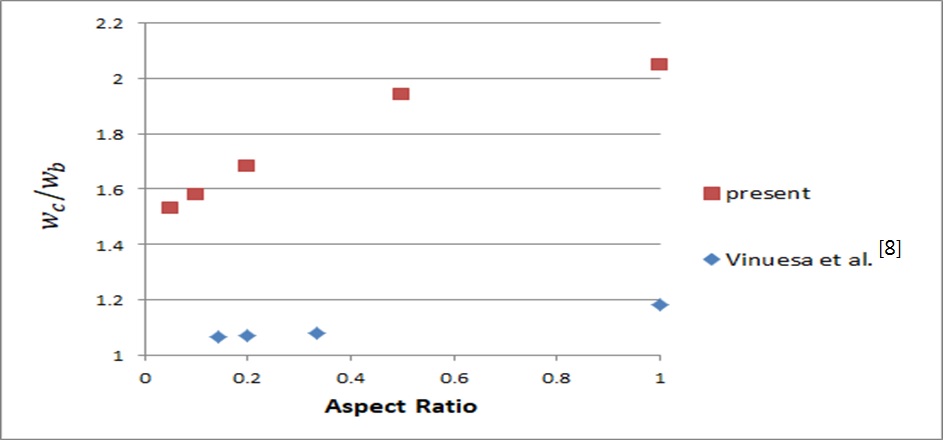
Variation of the center velocity normalized by the bulk velocity with respect to the aspect ratio of the duct

종횡비가 증가함에 따른 중심속도 증가는 Vinuesa et al.^[13]이 난류 유동 연구에서 설명한 바와 같이 좁은 면에서의 경계층이 덕트 중심부 유동을 가속화하는 효과가 있다는 사실과 관련이 있다고 볼 수 있다. 또한 Fig. 2에서와 같이 Vinuesa et al.^[8]의 난류값을 현재 층류 계산 결과와 비교할 때 종횡비에 따라 난류 유동에서의 비율 변화는 크지 않지만 층류 유동에서의 비율 변화는 상대적으로 더 크게 나옴을 확인할 수 있다.

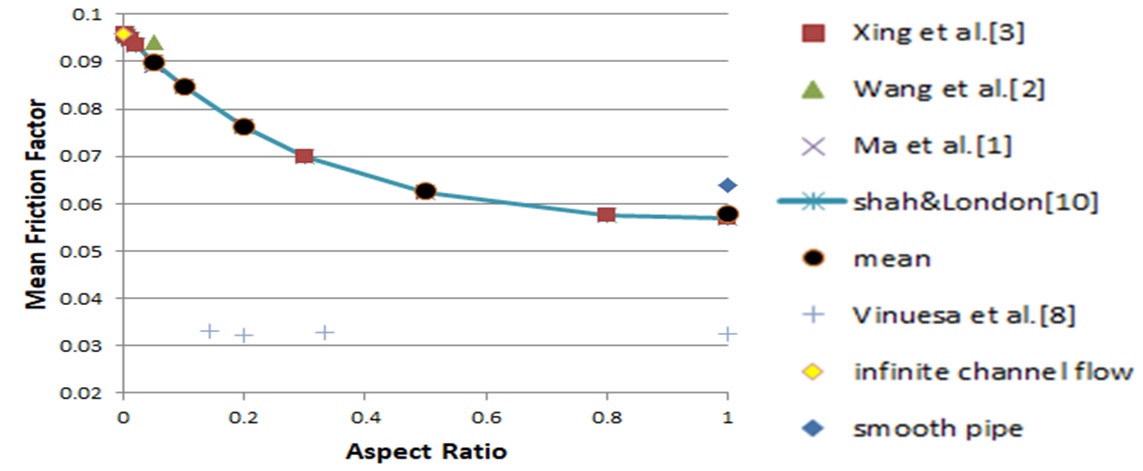
Fig. 3은 종횡비에 따른 완전발달영역에서의 평균마찰계수($$ f=\frac{8\tau }{\rho V^2}$$, τ는 벽면의 전단응력, ρ는 유체밀도)를 보여준다. Fig. 3에는 비교를 위하여 Xing et al.^[6] 등 기존 결과값을 같이 표시하였다. 참고로 Shah & London 방정식^[14]은 식 (1)에 제시되는 바와 같다.

Fig. 3

Variation of the mean friction factor with respect to the aspect ratio of the duct

식 (1)에 대한 점근값을 살펴보면, AR=0일 때 $$ f=\frac{96}{Re}$$이 되어 무한 평판 채널값과 같아지며 AR=1일 때는 $$ f=\frac{57}{Re}$$이 된다.

Fig. 3에서 볼 수 있듯이 본 계산 결과는 기존 이론이나 실험 결과들과 잘 일치함을 알 수 있다. Fig. 3에 따르면 층류 덕트 유동에서는 종횡비가 감소할수록 평균 마찰계수가 증가하게 되며, 최소종횡비인 0.05에서는 무한평판유동의 마찰계수값과 가까워지는 것을 확인할 수 있다. 또한 종횡비가 1일 때는 $$ f\approx \frac{57}{Re}$$로, 이 값은 Moody 선도에서 얻을 수 있는 값(smooth pipe)와 유사한 값이다. 참고로 Vinuesa et al.^[13] 논문에 제시된 난류 유동에서는 종횡비에 따라 마찰계수는 큰 변화가 없음을 확인할 수 있다. 이런 결과는 난류 유동에서는 종횡비에 상관없이 수력직경이 마찰계수를 예측하기 위한 길이 스케일이 될 수 있는 반면, 본 연구에서 동일한 Reynolds 수를 고려한다는 점을 감안할 때 층류에서는 수력직경이 마찰계수 예측을 위한 적절한 길이 스케일이 될 수 없음을 알 수 있다.

Muzychka and Yovanovich^[12]는 다양한 단면을 가지는 내부 유동 마찰계수가 단면 면적을 이용한 길이 스케일로 정리될 수 있다는 내용을 보고하였다. Fig. 4는 Muzychka and Yovanovich^[12]에 따라 마찰계수를 정리한 것이다. 여기서 Reynolds 수는 $$ \frac{V\sqrt{A}}{v}$$로 정의된다. 여기서 A는 직사각형 덕트 단면적이다.

Fig. 4

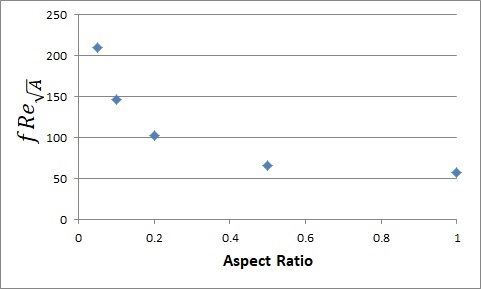
Variation of the friction factor times the Reynolds number based on the duct area with respect to the aspect ratio of the duct

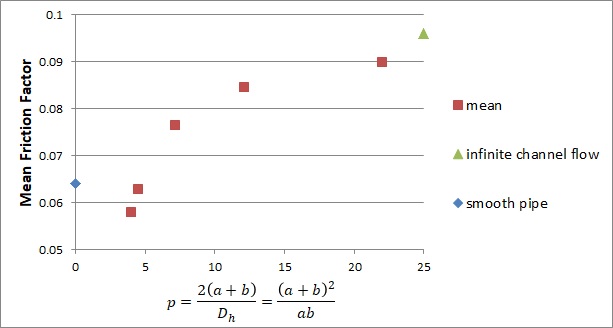
종횡비에 따른 평균마찰계수 변화를 다른 관점에서 살펴보기 위하여, 수력직경 대비 덕트 둘레길이에 따른 평균마찰계수를 그리면 Fig. 5와 같다. 원형 단면을 가지는 매끈한 파이프의 경우, 수력직경 대비 둘레길이는 π이며, 무한 평판 채널은 ∞의 값을 가진다. Fig. 5에서 볼 수 있듯이, 둘레길이가 증가할수록 평균마찰계수는 증가하게 되나, 증가율은 둘레길이가 작을 때 더 크게 나타난다. Fig. 5에서 볼 수 있듯이, 둘레길이가 증가할수록 평균마찰계수는 증가하게 되나, 증가율은 둘레길이가 작을 때 더 크게 나타난다. 다시 말하면 둘레길이가 큰 영역에서는 덕트 내 유동에 좁은 면의 영향을 거의 무시할 수 있으나, 둘레 길이가 10 이하로 줄어들게 되면서 좁은 면의 영향이 점차 나타나게 되며 둘레길이가 5~10 영역에서 좁은 면의 영향이 급격히 증가하게 된다. 이와 같이 덕트 내 유동 마찰 특성은 넓은 면과 좁은 면 상호 관계에 따라 크게 좌우된다.

Fig. 5

Variation of the mean friction factor with respect to (a + b)2/ab.

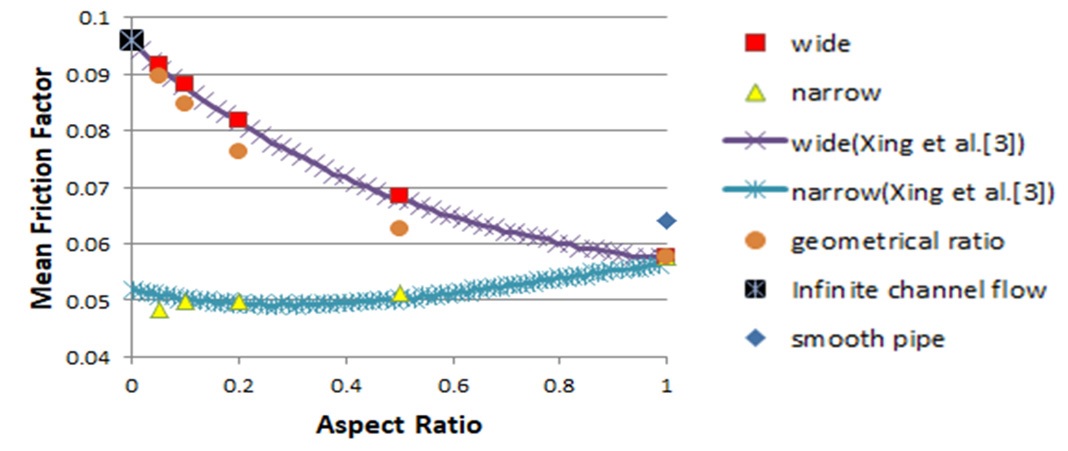
Fig. 6은 덕트의 넓은 면과 좁은 면에서의 종횡비에 따른 평균 마찰계수 변화를 보여준다. Fig. 6에서 볼 수 있듯이 덕트의 넓은 면에서는 종횡비가 감소할수록 마찰계수가 증가했으며 최소 종횡비인 경우 무한 평판 채널유동의 마찰계수 값과 유사함을 확인할 수 있다. 반면 덕트의 좁은 면에서는 넓은 면과 비교하여 상대적으로 종횡비에 따른 변화가 작으며, 또한 종횡비가 감소함에 따라 평균 마찰계수도 감소하게 된다. 좁은 면에서의 마찰계수 변화는 넓은 면에서의 마찰계수 변화보다 작은 관계로 전체적인 영향은 작다고 할 수 있다. 결과적으로 종횡비가 작을 때 전체평균 마찰계수는 넓은 면의 영향을 많이 받아서 Fig. 3에서 보는 바와 같이 종횡비가 감소함에 따라 평균 마찰계수가 증가하는 것으로 판단된다. 이는 넓은 면이 좁은 면보다 덕트 둘레길이에 차지하는 비중이 기하학적으로 크기 때문으로 이해될 수 있다. 이를 확인하기 위하여, 넓은 면에서의 마찰계수 대비 좁은 면에서의 마찰계수 와 넓은 면 대비 좁은 면 기하학적 비율을 Fig. 6과 같이 비교해 보았다. Fig. 6에서 볼 수 있듯이 넓은 면에서의 마찰계수 비중은 넓은 면의 기하학적 비중보다는 큰 것을 알 수 있으며, 이런 경향은 종횡비가 0.1~0.4 범위에서 크게 나타나게 된다.

Fig. 6

Variation of wide and narrow side friction factor with respect to the aspect ratio of the duct.

Fig. 7은 종횡비에 따른 덕트 넓은 면과 좁은 면에서의 벽면 마찰계수 분포를 보여준다. Fig. 6의 종횡비에 따른 평균 마찰계수 변화에서 유추할 수 있듯이, 종횡비에 따라 덕트의 넓은 면에서의 마찰계수 분포와 비교하여 좁은 면에서의 마찰계수 분포는 상대적으로 변화폭이 작다.

Fig. 7

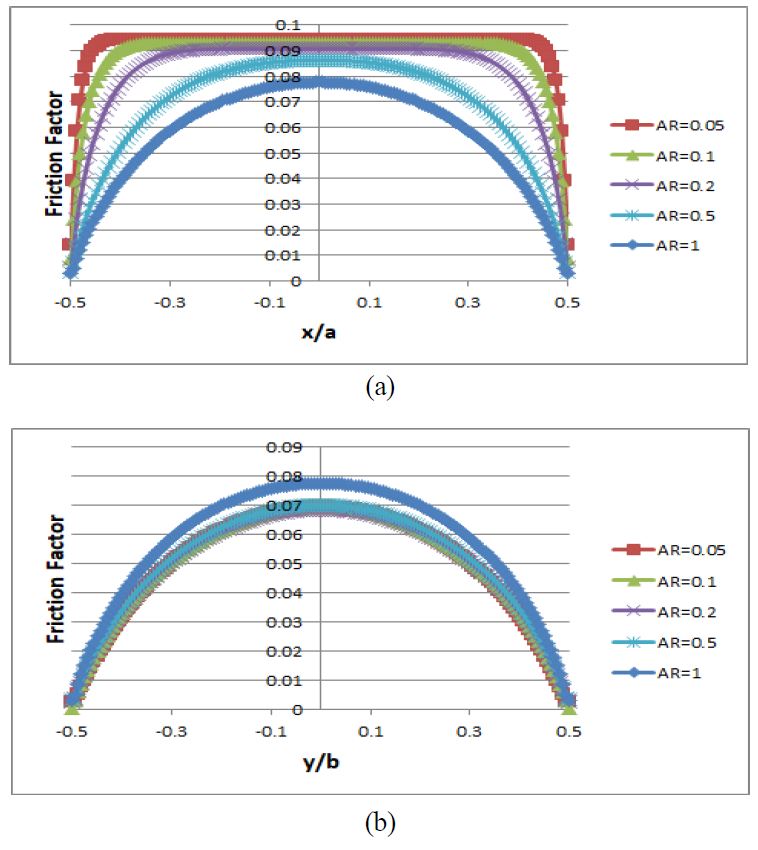
Variation of the friction factor with respect to the aspect ratio of the duct: (a) wide side; (b) narrow side.

덕트 넓은 면에 대해 종횡비가 1일 때 마찰계수 분포는 포물선 분포를 가지나, 종횡비가 감소하여 0.2 근처가 되면 중심 부근에서 평평한 분포를 가지게 된다. 이런 결과는 종횡비 0.2 이하에서 덕트중심 부근 영역에서는 유동이 상당히 2차원성을 가짐을 보여준다. 종횡비가 감소함에 따라 2차원적인 유동영역은 점차 확대되어 종횡비가 0.05일 때 80% 이상을 차지하게 된다. 따라서 종횡비가 감소함에 따라 넓은 면에서의 마찰계수가 증가하는 이유는 종횡비가 감소함에 따라 중심 부근에서 2차원적 유동이 형성되며 이런 유동이 종횡비가 1 근처일 때 형성되는 3차원적 유동보다 마찰계수가 큰 것에서 기인한다.

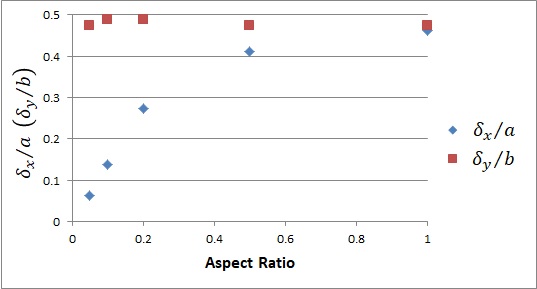
넓은 면에서의 2차원적 유동 특성과 관련지어 Fig. 8과 Fig. 9에서와 같이 덕트 넓은 면과 좁은 면에서의 속도 변화층 두께에 대해 추가로 살펴보았다. Fig. 8은 덕트 완전발달 유동영역에서 xy 평면에서의 축방향 속도 등고선도를 보여준다. 본 연구에서는 Fig. 8에서 볼 수 있는 바와 같이 속도 변화층 두께(δ_x, δ_y)를 넓은 벽면과 좁은 벽면의 중심에서 최대 속도까지 도달하기까지의 거리로 하였다. 이때 좁은 면의 중심에서 최대속도까지의 거리를 δ_x, 넓은 면의 중심에서 최대속도까지의 거리를 δ_y라 한다.

Fig. 8

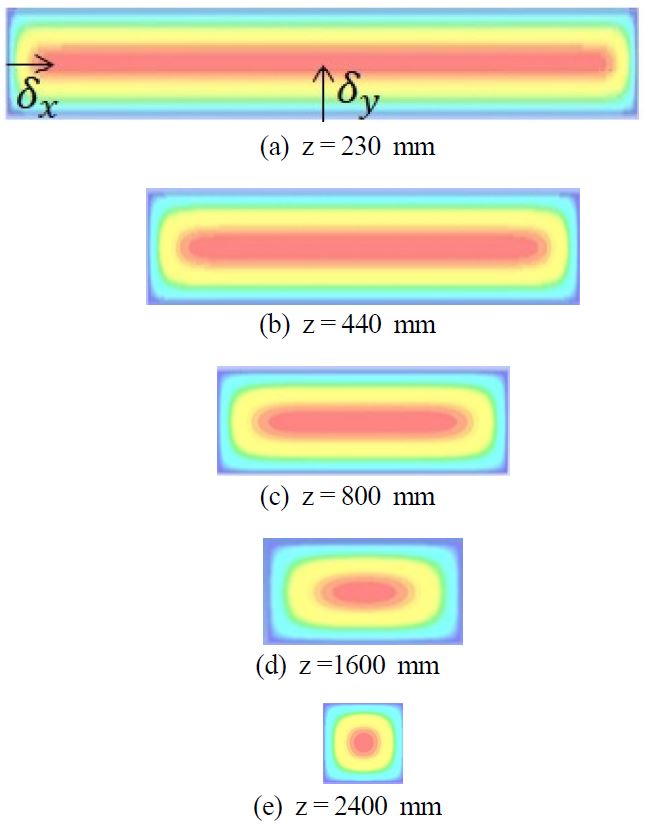
Contours of axial velocity in the fully developed region: (a) AR=0.05; (b) AR=0.1; (c) AR=0.2; (d) AR=0.5; (e) AR=1

Fig. 9

Variations of wide and narrow side velocity layer thickness

Fig. 9에서 볼 수 있듯이 좁은 면에서의 속도 변화층 두께는 종횡비에 따라 거의 변화하지 않으나, 넓은 면에서의 속도 변화층 두께는 종횡비가 감소함에 따라 크게 감소함을 알 수 있다. 최소 종횡비인 0.05일 때 속도경계층 두께는 약 0.1이며, 이는 중심점을 기준으로 약 80% 영역에서는 일정한 속도를 관찰할 수 있다는 것을 의미한다. 이는 앞에서 서술한 바와 같이 본 연구에서 고려한 최소 종횡비 0.05 조건에서는 약 80% 영역에 대해 유동이 2차원 특성을 가짐을 보여준다.

Fig. 10은 덕트 입구의 넓은 면과 좁은 면의 중심에서 출구의 넓은 면과 좁은 면의 중심까지 축방향을 따른 벽면 전단응력 변화를 보여준다. Fig. 10에서 볼 수 있듯이 덕트 넓은 면과 좁은 면에서의 벽면 전단 응력은 축방향을 따라 전단응력이 점차 감소하다 일정값에 수렴하는 것을 알 수 있다. 이런 벽면 전단응력 분포를 이용하며 축방향 중심속도를 이용한 입구길이와 달리, 넓은 면과 좁은 면에 따라 입구길이를 각각 분석할 수 있다.

Fig. 10

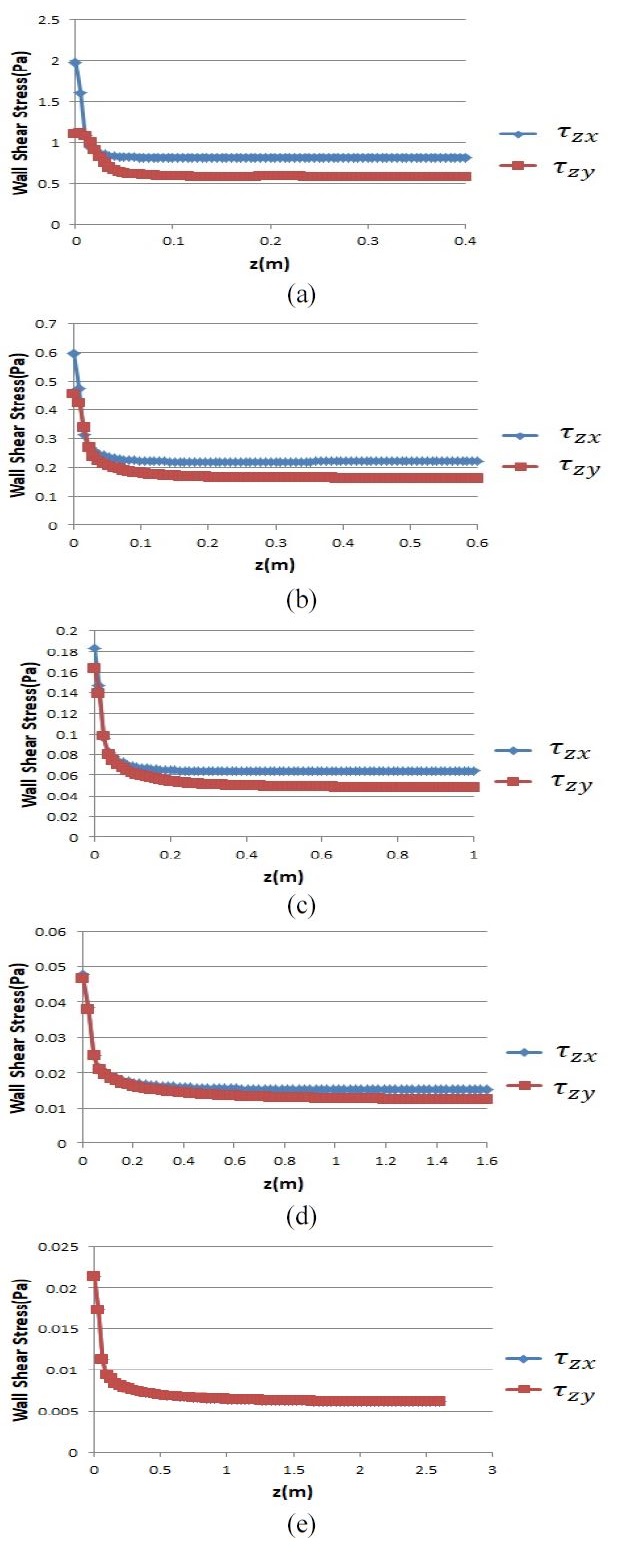
Variation of the wide and narrow side wall shear stress from the inlet to outlet: (a) AR=0.05; ; (b) AR=0.1; (c) AR=0.2; (d) AR=0.5; (e) AR=1

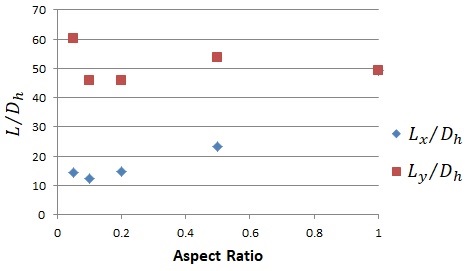
Fig. 11은 벽면 전단응력 분포를 기준으로 넓은 면과 좁은 면에서의 입구길이를 종횡비에 따라 나타낸 것이다. Fig. 11에서 좁은 면에서의 입구길이는 종횡비와 상관없이 약 50~60으로 거의 일정한 값을 가지나, 넓은 면에서는 종횡비가 감소함에 따라 입구길이가 점차 감소하게 된다. 따라서 종횡비가 작을 때 덕트 넓은 면 근처의 유동이 먼저 완전발달하게 되며 좁은 면 근처의 유동이 다음으로 완전발달하게 된다고 할 수 있다. 또한 Table 3에 종횡비가 0.05일 때 중심속도 기준으로 판정한 입구길이 L=20.06D_h는 종횡비가 작을 때 좁은 면에서의 벽면 전단응력으로 판단한 완전발달길이보다 작음을 통해, 종횡비가 작을 때 전반적으로 덕트 내 유동은 좁은 면의 영향을 받기는 하지만, 그 영향이 전반적으로 크지는 않음을 다시 한번 확인할 수 있다. 또한 넓은 면에서의 마찰계수로 판정한 입구길이가 중심속도 기준으로 판정한 입구길이보다 작다는 사실은 Vinuesa et al.^[13] 난류 결과와 유사하다.

Fig. 11

Ratio of entrance length based on the wall shear stress and the hydraulic diameter with respect to the aspect ratio of the duct: Lx ; entrance length based on the wall shear stress on the narrow side, Ly ; entrance length based on the wall shear stress on the wide side

4. 결 론

본 연구에서는 종횡비에 따른 덕트 내 층류유동 특성을 수치해석을 이용하여 연구하였다. 본 연구에서 고려한 종횡비는 0.05~1로, 태양전지, 연료전지 등에서 고려되는 범위를 포괄하고 있다.

본 연구 결과에 따르면, 덕트 내 층류유동 마찰 특성은 종횡비에 따라 크게 영향을 받는다. 이는 덕트 내 난류유동 특성과는 차이를 보이는 것으로, 문헌에 따르면 난류유동에서는 종횡비에 상관없이 수력직경 기반 Reynolds 수가 같은 경우에는 평균 마찰 계수가 거의 유사하다. 또한 기본적으로 덕트 내 층류유동은 종횡비에 따라 넓은 면의 영향을 많이 받는 2차원적 유동과 좁은 면의 영향을 많이 받는 3차원적 유동의 결합으로 마찰계수가 결정됨을 본 연구를 통해 파악하였다. 결과적으로 넓은 면의 영향이 상대적으로 큰 종횡비가 작은 경우에는 평균 마찰계수 등이 무한 평판 값들과 유사하게 된다. 그러나 좁은 면의 영향이 커지는 종횡비가 큰 경우에는 파이프 유동 특성과 정성적으로 많은 유사성을 가지게 된다.

또한 본 연구에서는 중심선 속도 또는 벽면 마찰계수 분석을 통해 완전발달영역 길이에 대한 종횡비 영향에 대해서도 파악하였다. 종횡비가 1인 경우에는 중심선 속도 또는 벽면 마찰계수 분석 모두 덕트 수력직경으로 무차원화한 입구길이는 약 60 정도이다. 반면, 종횡비가 1보다 작아지게 되면 벽면 마찰계수 분석을 통해 알 수 있듯이 넓은 면과 좁은 면에서의 입구길이는 차이를 보이며, 넓은 면에서의 입구길이가 좁은 면에서의 입구길이보다 큰 것을 알 수 있다. 본 연구에서 고려한 경우 중 종횡비가 가장 작은 경우인 0.05을 보면 넓은 면에서의 입구길이는 약 60D_h이며, 좁은 면에서의 입구길이는 약 10D_h이다.

Acknowledgments

본 연구는 원자력안전위원회의 재원으로 한국원자력안전재단의 지원을 받아 수행한 원자력안전연구사업의 결과입니다(Nuclear Safety Research Center Program: 1305011).

References

• Kim, J.-S., Sung, I.-H., Kim, D.-E., 2002, Fabrication of Micro-fluidic Channels Using a Flexible and Rapid Surface Micro-machining Technique, J. Korean Soc. Manuf. Technol. Eng., 11:4 97-101.
• Kang, I. B., Kim, H. J., Kim, B. H., Seo, Y. H., 2014, Microparticle Separator Based on Dean Vortex in Spiral Microchanel, J. Korean Soc. Manuf. Technol. Eng., 23:6 555-560. [https://doi.org/10.7735/ksmte.2014.23.6.555]
• Papautsky, I., Ameel, T., Frzier, A. B., 2001, A Review of Laminar Single-phase Flow in Microchannels, Proceedings of 2001 ASME International Mechanical Engineering Congress and Exposition 2001, 1-9.
• Ma, J., Li, L., Huang, Y., Liu, X., 2011, Experimental Studies on Single-phase Flow and Heat Transfer in a Narrow Rectangular Channel, Nucl. Eng. Des., 241:8 2865-2873. [https://doi.org/10.1016/j.nucengdes.2011.04.047]
• Wang, C., Gao, P., Tan, S., Wang, Z., Xu, C., 2012, Experimental Study of Friction and Heat Transfer Characteristics in Narrow Rectangular Channel, Nucl. Eng. Des., 250 646-655. [https://doi.org/10.1016/j.nucengdes.2012.06.029]
• Xing, D., Yan, C., Wang, C., Sun, L., 2013, A Theoretical Analysis about the Effect of Aspect Ratio on Single-phase Laminar Flow in Rectangular Ducts, Prog. Nucl. Eng., 65 1-7. [https://doi.org/10.1016/j.pnucene.2013.01.003]
• Park, H., Kim, J., Hong, M., 2008, A Study on the Flow Velocity of Micro Channels Depending on Surface Roughness, J. Korean Soc. Manuf. Technol. Eng., 17:1 59-64.
• Vinuesa, R., Bartrons, E., Chiu, D., Dressler, K. M., Rudei, J.-D., Suzuki, Y., Nagib, H. M., 2014, New Insight into Flow Development and Two Dimensionality of Turbulent Channel Flows, Exp. Fluids, 55:1759 1-14. [https://doi.org/10.1007/s00348-014-1759-8]
• Bhushan, B., Singh, R., 2010, A Review on Methodology of Artificial Roughness Used in Duct of Solar Air Heaters, Energy, 35:1 202-212. [https://doi.org/10.1016/j.energy.2009.09.010]
• Sahu, M. M., Bhagoria, J. L., 2005, Augmentation of Heat Transfer Coefficient by Using 90 Broken Transverse Ribs on Absorber Plate of Solar Air Heater, Renewable Energy, 30:13 2057-2073. [https://doi.org/10.1016/j.renene.2004.10.016]
• Yuan, J., Rokni, M., Sunden, B., 2001, Simulation of Fully Developed Laminar Heat and Mass Transfer in Fuel Cell Ducts with Different Cross-Sections, Int. J. Heat Mass Transfer, 44:21 4047-4058. [https://doi.org/10.1016/S0017-9310(01)00052-7]
• Muzychka, Y. S., Yovanovich, M. M., 2009, Pressure Drop in Laminar Developing Flow in Noncircular Ducts: A Scaling and Modeling Approach, ASME J. Fluids Eng., 131:11 11105-11115. [https://doi.org/10.1115/1.4000377]
• Vinuesa, R., Noorani, A., Lozano-Duran, A., El Khoury, G. K., Schlatter, P., Fischer, P. F., 2014, Aspect Ratio Effects in Turbulent Duct Flows Studied Through Direct Numerical Simulation, J. Turb., 15:10 677-706. [https://doi.org/10.1080/14685248.2014.925623]
• Shah, R. K., London, A. L., 1978, Laminar Flow Forced Convection in Ducts: A Source Book for Compact Heat Exchanger Analytical Data, Academic Press, New York.
• Muzychka, Y., Yovanovich, M., 2004, Laminar Forced Convection Heat Transfer in the Combined Entry Region of Non-circular Ducts, ASME J. Heat Transfer, 126:1 54-61. [https://doi.org/10.1115/1.1643752]