기어 정밀도를 고려한 e-PGS 피니언의 굽힘 강도설계
Abstract
An accurate estimation of the tooth load is inevitable for an optimum design of high-quality gears. Because only a fraction of the total load is shared by each pair, when there is contact in more than one pair during transmission, it can be estimated with reasonable accuracy through the load sharing factor. The first attempt of the load distribution comparison during the double teeth engagement of an external pinwheel gear set (e-PGS) was performed by considering the load sharing factor. Subsequently, the tooth root bending stress (TRBS) for fatigue failure design was investigated to determine the characteristics of the tooth fatigue by varying the center distance modification coefficient (CDMC). The TRBS could be lowered significantly by increasing the CDMC and the manufacturing of high-quality gears. Moreover, it was found that the behavior of TRBS with the variation of the gear accuracy grade during the contact of two teeth differed significantly.
Keywords:
e-PGS (external pinwheel gear set), Load sharing factor, Gear accuracy grade, Center distance modification coefficient, Tooth root bending stress1. 서 론
최근 거스 기어(girth gear)용 대형 링 기어 치형을 핀 또는 롤러 치형으로 대체한 핀 휠과 피니언이 외접 치합하는 핀 휠 기어쌍(external pinwheel gear set, 이하 e-PGS)[1]이 유지 보수 및 제작 용이성 측면에서 주목을 받고 있다.
하지만 로터리 킬른(rotary kiln), 하역기(ship unloader), 화력발전소용 공기예열기, 가스-가스 재열기 등 다양한 산업 현장에서 적용하고 있는 e-PGS 피니언 치형은 스프로킷 등의 합성치형을 채택하고 있기에 치 물림 시 충격이 불가피하고 내구수명이 짧은 문제점 등이 있었다. 지금까지의 e-PGS 피니언 관련 자료조사 결과, 합성치형 설계방법[2,3]과 중심거리증가계수(center distance modification coefficient, 이하 CDMC)의 개념을 도입한 엄밀치형 설계 및 강도설계[1,4-9] 정도의 극소수 연구만이 수행되었다. 또 물림률(contact ratio, ϵ)이 1 < ϵ < 2인 대부분의 기어 구동 시 LPSTC(lowest point of single tooth contact), HPSTC(highest point of single tooth contact)를 경계로 전달하중의 분담(sharing)과 전담의 전환이 주기적으로 발생한다. 특히 전달하중 분담구간에서의 하중분포는 치형수정(profile modification) 및 기어 정밀도(gear accuracy grade)의 함수로 알려져 있고, 높은 신뢰도를 갖는 고품질 기어 설계를 위해서는 정확한 하중분포의 고려가 필수불가결하다.
이에 본 논문에서는 기어 정밀도를 고려하지 않은 기존 연구[9]와 고려했을 때의 CDMC에 따른 굽힘응력 비교 고찰을 통하여 e-PGS 피니언의 굽힘 강도설계에 일조하고자 한다.
2. 기어 정밀도를 고려하지 않은 접촉력
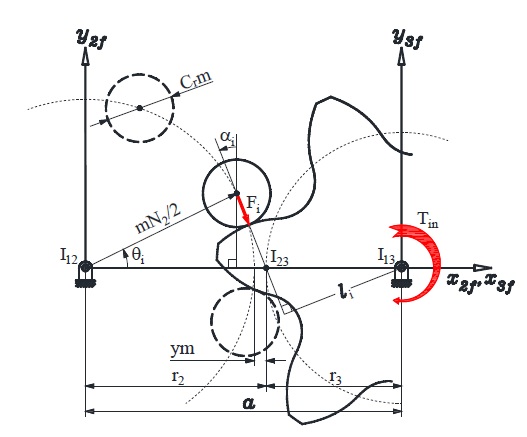
e-PGS는 일정 각속도비 또는 피치점(pitch point, I23)을 갖는 접촉 3절기구(Fig. 1 참조)의 일종으로서, 엄밀치형은 기어 모듈(m), 핀 휠의 롤러 개수(N2), 피니언의 잇수(N3), 롤러직경계수(Cr), CDMC(y), 이높이계수(β)로 구성된 6개의 설계제원들을 고려하여 속도의 순간중심과 동차좌표변환을 통해 결정[1,6-9]할 수 있다. 이때 중심거리 a는 a0=m(N2+N3)/2보다 크게 설계하여야 엄밀치형을 획득할 수 있다. 즉 CDMC y=(a - a0)/m는 반드시 양수 값을 가져야 한다.
Fig. 1과 같이 e-PGS 피니언이 회전중심 I13에 주어진 입력 토크 Tin에 의해 ϕ3(roll angle)만큼 회전한 경우, 즉 임의의 회전각 θi에 위치한 i-번째 롤러와 피니언과의 접촉력 Fi는 일정 접촉강성(equal mesh stiffness)을 고려한 부정정 문제 접근[1,6-9]을 통해 다음과 같이 결정할 수 있다.
| (1) |
여기서 n은 핀 휠과 피니언 간의 접촉 개소를 의미하고, li는 모멘트 팔로 압력각 αi를 고려하여 다음과 같이 결정된다.
| (2) |
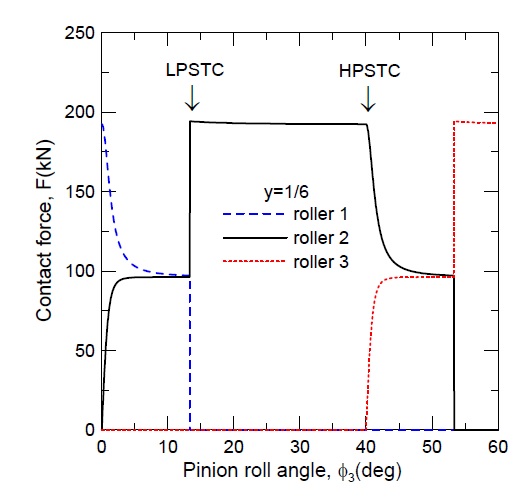
e-PGS 구동 시 식 (1)에 의한 접촉력 변화를 확인하기 위해 실제 제작운용 중인 하역기 선회용 거스 기어의 제원(Table 1 참조)을 고려하여 피니언 회전에 따른 접촉력 변화를 Fig. 2에 도시하였다. 초기 3곳의 접촉개소(=2[β]+1)를 가지며, 이때 피니언의 회전에 따라 물림이탈이 빠른 시간 순서로 핀 휠 롤러들의 접촉번호를 지정하였다. 또 이높이계수 β의 범위가 1 ≤ β < 2일 때 물림률은 ϵ=3-2/β로 평가[1]된다. 따라서 Fig. 2의 물림률이 1.5이기에 각각 50%의 물림구간에서 두 쌍의 기어 치 또는 한 쌍의 기어 치들이 전달하중을 분담 또는 전담한다. 또 두 쌍의 기어 치들이 하중을 분담하는 구간(double tooth contact, DTC)에서 한 쌍의 기어 치들이 하중을 전담하는 구간(single tooth contact, STC)으로의 하중전환(또는 STC → DTC 하중전환)이 일어날 때 주기적이고 지속적인 급격한 하중변화를 겪게 되며, 이로 인해 다양한 피로파손이 야기된다.
또 EMS 가정하의 식 (1)의 경우, STC 구간(LPSTC, HPSTC)에서의 접촉력은 최대 접촉력 Fmax(=Tin/lSTC)와 거의 동일하면서 일정한 값을 가지는 반면, DTC 하중분담구간에서의 하중의 크기는 대략 Fmax/2임을 알 수 있다.
3. 하중분담계수
통상 기어 정밀도(gear quality class, Av)는 피치 오차(pitch deviation), 치형 오차(profile deviation), 잇줄 오차(lead deviation), 흔들림 오차(run-out deviation) 등을 종합적으로 검토하여 결정되며, 기어의 사용목적에 따라 적절한 기어 정밀도를 고려하여 제작하게 된다. 하지만 전 절 Fig. 2의 하중분포는 기어 이의 정밀도를 고려하지 않았기에 실제 기어 이가 받는 하중과는 상당한 차이가 있다.
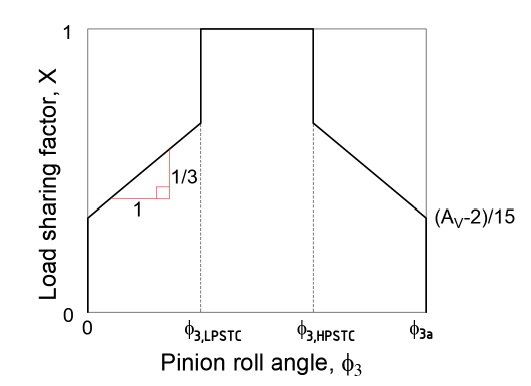
즉 ISO 7급 이하(Av ≤ 7)의 정밀급 기어의 경우 DTC 구간에서의 하중분포는 기어 진입 시 Fmax/2의 하중분담이 아니라 (Fmax/3 → 2Fmax/3), 기어 퇴거 시 (2Fmax/3 → Fmax/3)의 선형적인 하중분담의 변화[10-13]를 보인다. 또 ISO 8급 이상 기어의 DTC 구간 하중분포는 ISO 7급 이하와 마찬가지로 선형적이기는 하나 분담하중들이 등급에 비례하여 커진다. 이를 하중분담계수(load sharing factor, X)를 도입하여 설명한 그림이 Fig. 3이다. 여기서 하중분담계수 X = F/Fmax로 정의된다.
따라서 임의의 회전각 θi에 위치한 i-번째 롤러와 피니언과의 접촉력 Fi는 하중분담계수를 고려하여 다음과 같이 결정할 수 있다.
| (3) |
여기서
| (4) |
이때 AY=(Av - 2)/15이며 Av ≤ 7인 정밀급 기어의 경우 Av = 7을 적용한다. 또 θ3i = (N2/N3) θi = ([β]+1-i)ϕ3p+ϕ3를 나타낸다.
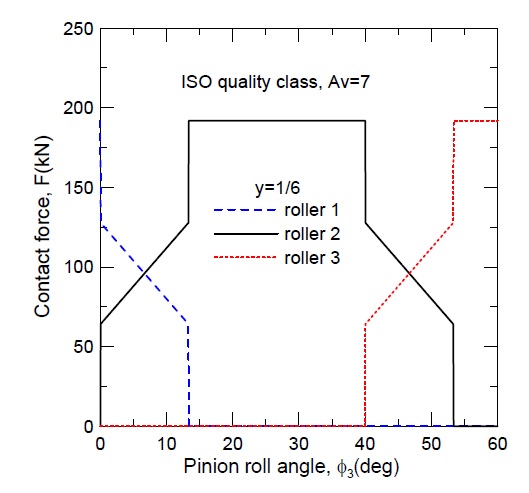
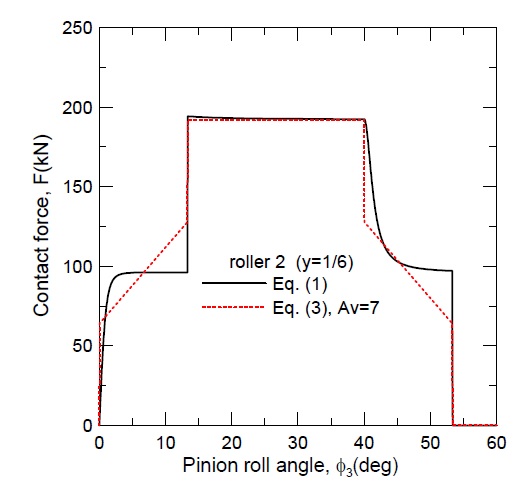
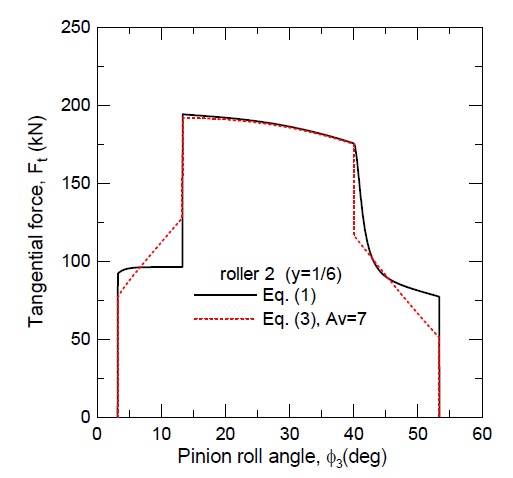
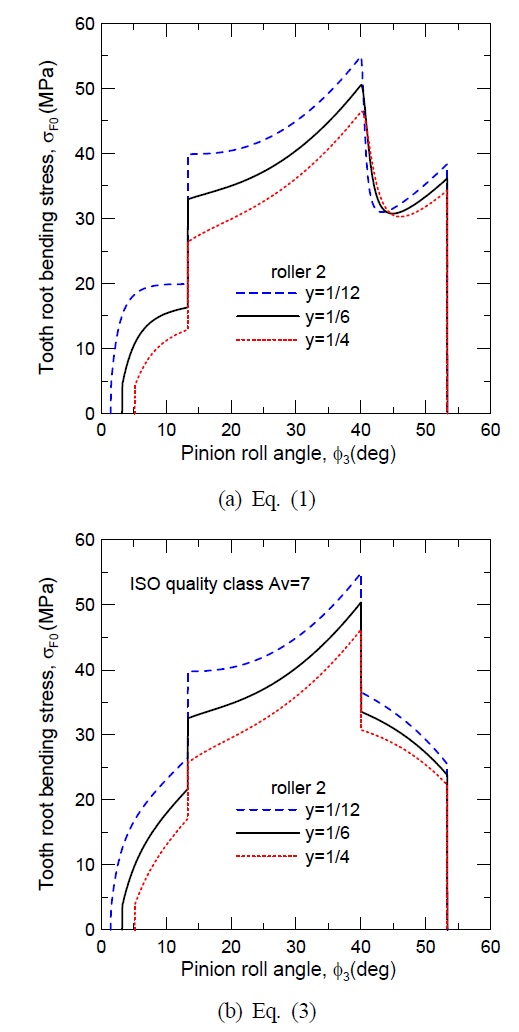
Fig. 4는 Table 1의 설계제원과 식 (3)을 기반으로 한 ISO 7급 기어의 접촉력 변화이다. 기어 정밀도를 고려하지 않은 Fig. 2와는 하중분담구간(DTC)에서 하중분포가 상당한 차이가 있음을 확인할 수 있다. 이를 보다 명확히 하기 위해 롤러 2와 접촉하는 피니언에 대한 식 (1)과 식 (3)의 하중분포를 Fig. 5에 동시에 도시하였다. DTC 구간에서의 확연한 차이를 재확인할 수 있으며, STC 구간에서의 하중분포는 거의 동일함을 확인할 수 있다.
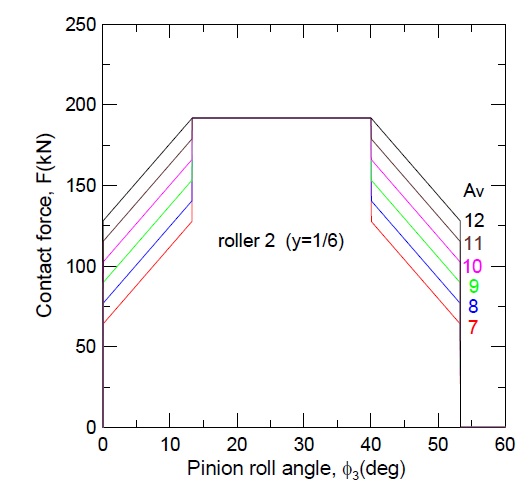
Fig. 6은 기어 정밀도에 따른 롤러 2와의 접촉력의 변화를 도시하였다. 식 (4)의 AY값을 통하여 예측할 수 있듯이 기어 정밀도가 낮아질수록 DTC 구간에서의 분담하중이 증가함을 확인할 수 있다. 따라서 DTC 구간에서의 하중 및 응력을 낮추기 위해서는 높은 제작정밀도가 요구된다.
4. 굽힘응력
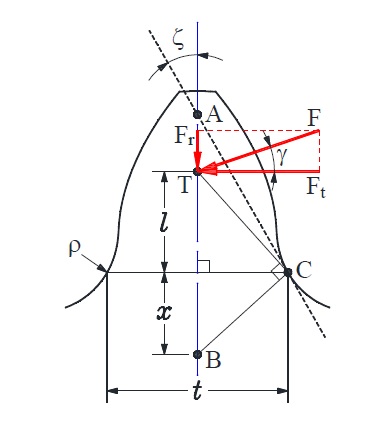
이뿌리 부 인장 굽힘응력(tooth root bending stress, 이하 TRBS)으로 인한 기어 이의 절손(breakage)은 치명적 파손현상으로, 이의 내구설계를 위해서는 위험단면(critical section)의 위치와 현 이두께(t, Fig. 7 참조)의 여하한 결정이 관건이다. 본 논문에서는 하중점의 위치에 관계없이 치 중심선과 ζ = 30°의 각도를 이루는 직선이 기어 치에 내접하는 점(Fig. 7 의 점 C)을 통과하는 단면이 위험단면이 된다는 ISO 6336-3, DIN 3990-3, JGMA 401-01의 30° 접선법을 채택하여 모듈기반 치형계수(tooth form factor, Y)를 결정[9]하였다. 이를 통해 다음과 같이 TRBS σF를 결정할 수 있다.
| (5) |
여기서 k∞는 Ko, Kv, Ks, Km, KB 등의 AGMA 보정계수[14]들을 고려한 전체 보정계수(overall derating factor)를 의미하며, σF0는 보정 전 공칭(nominal) TRBS이다. 또 Ft는 접선력(transmitted tangential load)이며, Yj는 형상계수(bending strength geometry factor)로 Y / YS의 값을 갖는다. 이때 YS는 이뿌리 부 피로응력집중을 고려한 ISO 6336-3의 응력수정계수(stress correction factor)로 다음과 같다.
| (6) |
여기서 L = t/l, qS=t/(2ρ)이고 ρ는 위험단면에서의 곡률반경을 의미한다. 또 1 ≤ qS < 8의 범위일 때 식 (6)은 유효하다.
그리고 식 (5)에서의 접선력 또는 굽힘하중 Ft는 다음과 같이 결정할 수 있다.
| (7) |
여기서 F는 식 (1) 또는 식 (3)의 접촉력이며, 하중각(load angle, Fig. 7 참조) γ는 다음과 같다.
| (8) |
이때 α는 해당 하중위치에서의 압력각을 의미한다.
5. 결과검토
5.1 이뿌리 굽힘응력
Table 1의 주어진 설계제원에 대한 굽힘강도 설계를 수행하기 위해 식 (5)에서의 접선력 Ft와 형상계수 Yj를 순차적으로 검토하였다.
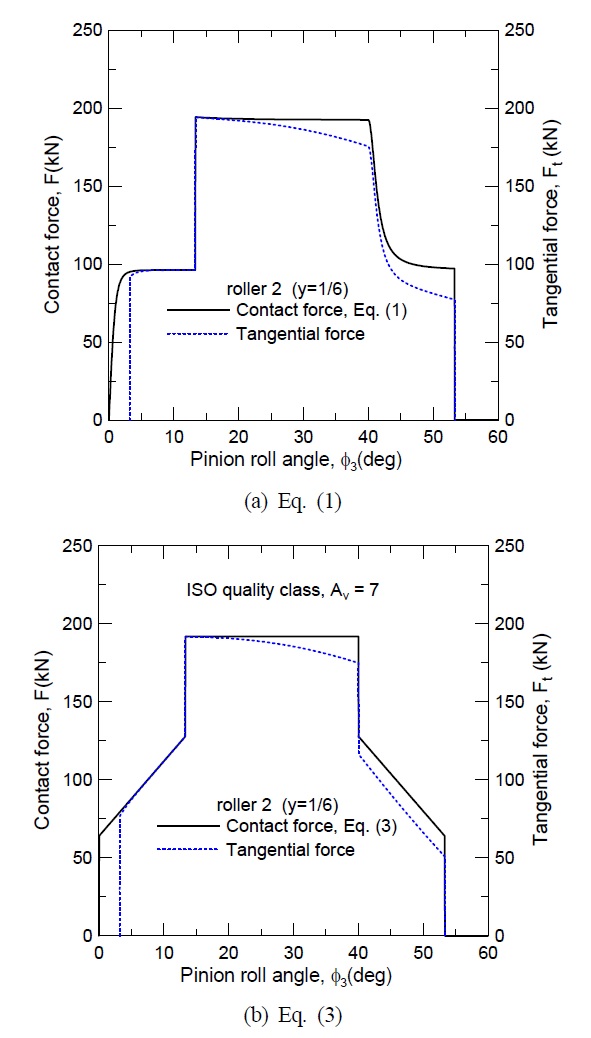
먼저 Fig. 8은 식 (1)과 식 (3)에 의해 롤러 2와의 접촉력(F)과 접선력(Ft)을 대비하여 도시한 그림으로 LPSTC 이전에서는 접선력(Ft)과 접촉력(F)이 거의 일치하나 LPSTC 이후 접선력(Ft)이 감소함을 확인할 수 있다. 이는 LPSTC를 지나 이의 물림이 진행될수록 하중각(γ)이 커짐에 기인한다. 또 기어 이의 굽힘에 관여하는 접선력(Ft)은 하중점(Fig. 7의 점 T)이 위험단면(Fig. 7의 점 C) 보다 낮은 위치에 있을 경우 유효하지 않기에 피니언 회전각이 약 3.2° 이상의 유의미한 접선력만이 Fig. 8에 반영되어 있음을 주목할 필요가 있다.
Fig. 9는 Fig. 8(a), (b)의 접선력(Ft)만을 고려한 그림이며, 기어 정밀도를 고려했을 경우 DTC 구간 내에서의 가파른 접선력(Ft) 증감 변화를 확인할 수 있다.
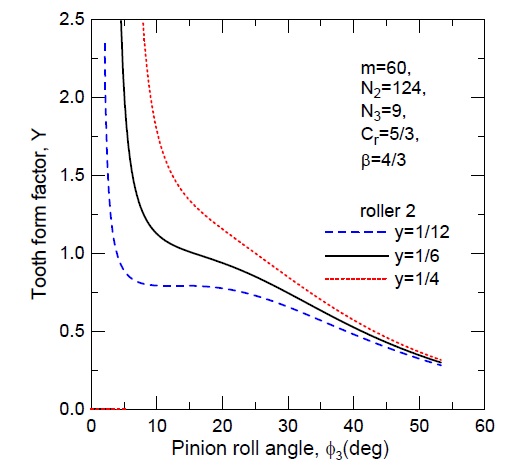
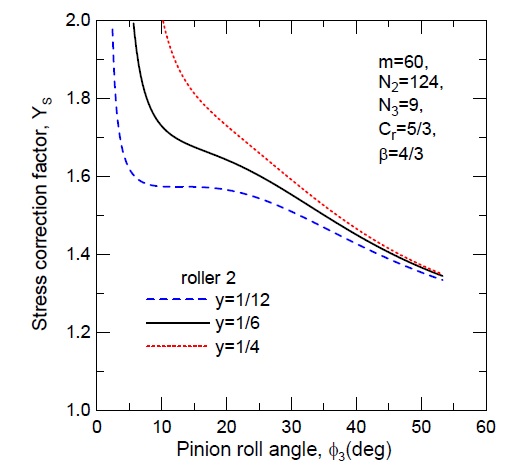
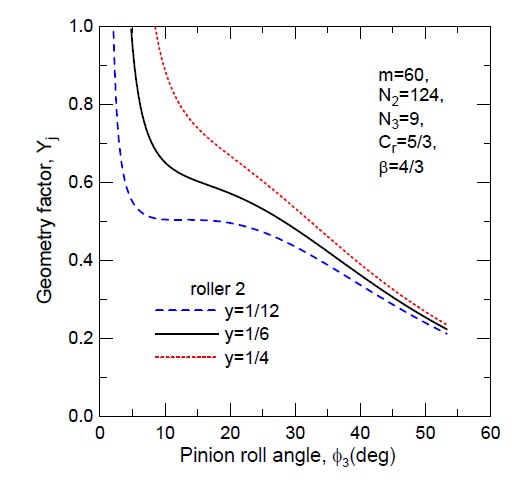
다음으로 피니언 회전에 따른 형상계수 Yj의 변화를 고찰하기 위해 치형계수(Y)와 응력수정계수(YS)의 변화를 Fig. 10과 Fig. 11에 제시하였다. 피니언 이뿌리부에서 이끝 부위로 물림이 진행되면서 치형계수(Y)와 응력수정계수(YS) 모두 감소하는 경향을 확인할 수 있다. 이에 의해 형상계수 Yj 또한 물림위치가 증가할수록 감소하고 있음을 Fig. 12에서 확인할 수 있다. 또 CDMC가 증가함에 따라 치형계수(Y), 응력수정계수(YS), 형상계수(Yj) 공히 증가함을 알 수 있다.
Fig. 13은 굽힘 강도설계를 위한 TRBS 결과를 식 (1)과 식 (3)에 기반하여 각각 도시한 그림들이다. 우선 CDMC가 증가함에 따라 TRBS는 감소함을 알 수 있다. 이는 CDMC 증가에 따라 Fig. 12와 같이 형상계수(Yj)의 증가에 기인한다. 또 최대 TRBS는 HPSTC에서 발생함을 확인할 수 있다. 이는 기어 이뿌리 절손은 STC 최고위치인 HPSTC에서의 접선하중에 기인한다는 기존 인벌류트 치형 연구결과와도 일맥상통한다.
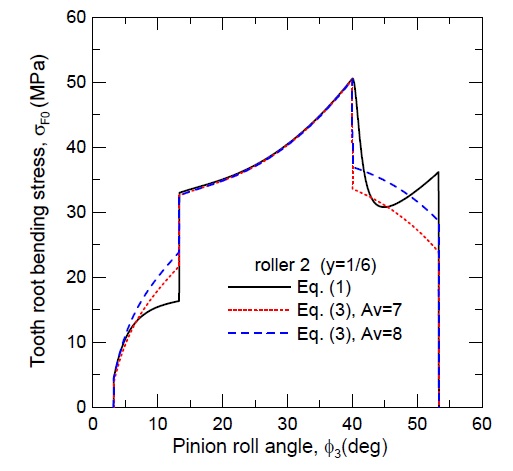
Fig. 14는 식 (1)과 식 (3)에 의한 Fig. 13의 각각의 결과들을 동시에 도시한 그림이다. 우선 식 (1) 또는 식 (3)에 따른 STC 구간에서의 TRBS 거동은 일치함을 알 수 있다. 반면 LPSTC 이전 DTC 구간에서는 식 (1)에 기반한 TRBS는 기어 정밀도를 고려한 TRBS 보다 과소평가됨을 확인할 수 있고, HPSTC 이후 DTC 구간에서는 TRBS의 변화경향이 극명하게 차이를 가짐을 확인할 수 있다. 즉 식 (1)에 의한 TRBS는 HPSTC 이후 감소하다 이끝으로의 물림이 진행되면서 다시 증가하는 반면, 기어 정밀도를 고려한 TRBS는 HPSTC 이후 물림이 종료될 때까지 감소하는 경향을 보인다. 이는 (Ft/Yj)의 증감에 기인한다. 즉 HPSTC 이후 접선력(Ft)의 감소폭이 형상계수(Yj)의 감소폭보다 큰 가 작은가에 따라 TRBS 거동이 달라진다.
또한 기어 정밀도가 낮아짐(Av 증가함)에 따라 DTC 구간에서의 TRBS는 증가함을 확인할 수 있다.
5.2 수명평가
본 논문에서는 ANSI/AGMA 2001-D04를 준용하여 e-PGS 피니언에 대한 굽힘강도 안전계수[14]를 다음과 같이 결정하였다.
| (9) |
여기서 St는 107 부하횟수, 99% 신뢰도를 갖는 보정 전 굽힘피로강도, YN은 굽힘강도 수명 보정계수, KT는 온도 보정계수, KR은 신뢰도 보정계수이다.
본 논문에서는 보정 전 굽힘피로강도 St = 151 MPa인 Grade 1 고주파 열처리강[14]을 고려하였다. 또 Table 1에 제시된 선회감속기 요구수명(B10 수명: 175,200 hr, Nreq=2.17×107 cycle)은 99% 신뢰도, 107 cycle과는 다르기에 신뢰도 보정계수 KR = 0.85(90% 신뢰도)를, 수명보정은 다음의 식을 고려하여 Table 2와 같이 안전계수들을 평가하였다.
| (10) |
그리고 최대 TRBS(σF,max)는 HPSTC에서의 공칭 TRBS σF0 값에 Table 1에 제시한 실제 운용환경을 고려한 보정계수 k∞=2.8을 반영하여 평가하였다.
Fig. 13으로부터 알 수 있듯이 CDMC가 증가하면 TRBS가 감소하기에 굽힘강도 안전계수(SF)가 증가함을 알 수 있다. 일반적인 기어 설계 시 굽힘강도 안전계수는 1.2 이상이 요구된다. 하지만 CDMC가 y=1/12와 같이 중심거리 증가 효과가 미미하거나 합성치형(y→0)[2,3]일 경우, 일반적인 기어 강도설계 기준(SF ≥ 1.2)을 충족하지 못함을 확인할 수 있다. 따라서 일정 값 이상의 CDMC 고려를 통해 e-PGS 피니언의 굽힘 피로수명을 확보할 수 있음을 알 수 있었다.
6. 결 론
본 연구에서는 기어 정밀도를 고려한 e-PGS 피니언의 굽힘강도 설계를 수행하였고, 그 결과를 요약하면 다음과 같다.
(1) 일정접촉강성 가정하의 접촉력과 하중분담계수를 고려한 접촉력은 하중전담구간(STC)에서는 거의 일치하였으나 하중분담구간(DTC)에서는 상당한 차이를 가지며 기어 정밀도가 낮을수록 분담하중이 증가함을 확인하였다.
(2) 또한 설계제원 중 중심거리증가계수의 증가에 따라 이뿌리 굽힘응력은 크게 감소하는 경향을 관찰할 수 있었고, 기어정밀도에 따라 하중분담구간(DTC)에서의 이뿌리 굽힘응력 거동은 큰 차이를 보임을 확인하였다.
최종적으로 본 논문에서 고려한 e-PGS 피니언의 경우 기어 제작정밀도를 높이고 일정 수준 이상의 적절한 중심거리증가계수 선정을 통해 요구되는 피로수명을 충족시킬 수 있음을 알 수 있었다.
References
- Shin, H. C., 2017, A Study on Pitting Life Estimation of Girth Gear based on e-PGS, Master’s Thesis, Changwon National University, Republic of Korea.
- Litvin, F. L., Fuentes, A., 2004, Gear Geometry and Applied Theory, 2nd ed., Cambridge University Press, London.
- Veja, A. D., 2012, Contributions Concerning the Roller Gearing Tooth Profile Generation, Balkan Journal of Mechanical Transmissions, 2:1 73-77.
-
Honda, H., Makino, H., 1994, Research on the Trochoidal Gears (1st Report), J. Jpn. Soc. Precis. Eng., 60:7 949-953.
[https://doi.org/10.2493/jjspe.60.949]

-
Honda, H., 1995, Research on the Trochoidal Gears (2nd Report), J. Jpn. Soc. Precis. Eng., 61:2 208-212.
[https://doi.org/10.2493/jjspe.61.208]

-
Kwon, S.-M., 2015, Contact Stress of Slewing Bearing with External Pinwheel Gear Set, J. Korean Soc. Manuf. Technol. Eng., 24:2 231-237.
[https://doi.org/10.7735/ksmte.2015.24.2.231]

-
Kwon, S.-M., Shin, H. C., 2016, Estimation of Contact Fatigue Life of a Girth Gear Based on Pinwheel, J. Korean Soc. Manuf. Technol. Eng., 25:4 245-252.
[https://doi.org/10.7735/ksmte.2016.25.4.245]

-
Kwon, S.-M., 2018, Contact Fatigue Life of Yaw Drive Pinion using e-PGS, Trans. Korean Soc. Mech. Eng. A, 42:6 557-563.
[https://doi.org/10.3795/KSME-A.2018.42.6.557]

-
Kwon, S.-M., Park, Y.-S., 2020, Strength Design of Slewing Drive Pinion for Ship Unloader, J. Korean Soc. Manuf. Technol. Eng., 29:5 386-392.
[https://doi.org/10.7735/ksmte.2020.29.5.386]

- Vullo, V., 2020, Gears - Volume 2: Analysis of Load Carrying Capacity and Strength Design, Springer Nature Switzerland AG, Switzerland.
-
Spitas, V., Papadopoulos, G. A., Spitas, C., Costopoulos, T., 2011, Experimental Investigation of Load Sharing in Multiple Gear Tooth Contact Using the Stress-Optical Method of Caustics, Strain, 47:s1 e227-e233.
[https://doi.org/10.1111/j.1475-1305.2008.00558.x]

-
Pedrero, J. I., Pleguezuelos, M., Artés, M., Antona, J. A., 2010, Load Distribution Model Along the Line of Contact for Involute External Gears, Mech. Mach. Theory, 45:5 780-794.
[https://doi.org/10.1016/j.mechmachtheory.2009.12.009]

-
Sanchez, M. B., Pedrero, J. I., Pleguezuelos, M., 2013, Critical Stress and Load Conditions for Bending Calculations of Involute Spur and Helical Gears, Int. J. Fatigue, 48:March 28-38.
[https://doi.org/10.1016/j.ijfatigue.2012.11.015]

- Budynas, R. G., Nisbett, J. K., 2015, Shigley’s Mechanical Engineering Design, 10th ed., McGraw-Hill, NY.

Professor in the School of Mechanical Engineering, Changwon National University.
His research interests are pin gearing and speed reducer.
E-mail: smkwon@changwon.ac.kr