광전송 매질에 대한 태양광 전송 이론식 구축과 실험에 의한 고찰

2.1 광전송 형상

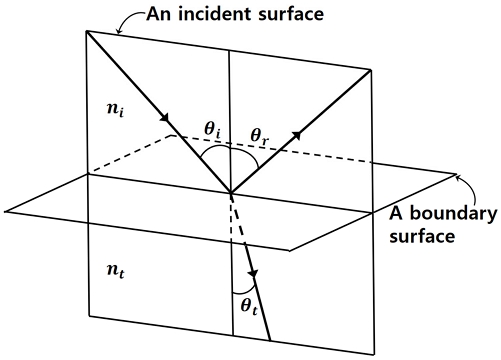
Fig. 1은 서로 다른 두 매질을 통과하는 빛의 굴절에 대한 스넬의 법칙(Snell’s law)을 나타내며 식(1)의 관계를 갖는다.

Fig. 1

A drawing of refraction and reflection at two types of dielectric interface

여기서 sinθ_t = 1 즉, θ_t = 90° 일 때 빛이 경계면을 투과하지 못하고 전반사하게 된다. 이 전반사하는 각도를 임계각이라 하며 θ_c로 나타내기로 하고 식(1)을 정리하면 임계각 θ_c는 식(2)와 같이 나타낼 수 있다.

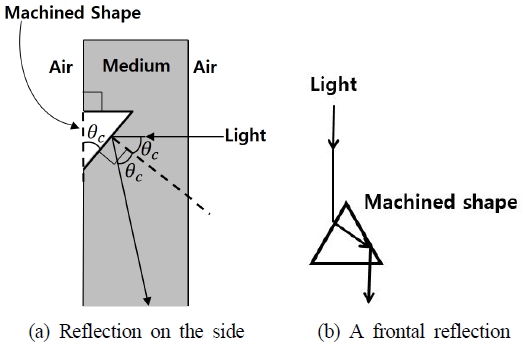
식(2)에서 n_i는 아크릴 재질의 굴절률이라 하고 n_t를 공기의 굴절률이라 하면 임계각 θ_c = 41.8^o가 된다. 그런데 빛을 한 방향으로 전반사시키기 위한 광전송용 형상으로 직각 삼각뿔이 적합하다고^[1] 하였으므로 여기서도 직각 삼각뿔을 광전송용 형상으로 채택한다. 따라서 임계각이 41.8^o가 되도록 아크릴 패널 표면에 하나의 직각 삼각뿔을 가공한다고 가정하면 Fig. 2와 같이 나타낼 수 있다. 즉, 임계각(θ_c)는 Fig. 2(a)와 같으며 아크릴 패널 위에서 직각으로 바라본 모습은 Fig. 2(b)와 같이 나타낼 수 있다.

Fig. 2

Reflective appearance of light by pattern type

2.2 광전송 에너지식 정립

태양광 전송패널에는 직각 삼각뿔을 패턴으로 가공한다고 가정하고 패널에 조사되는 빛은 패널 평면에 수직 방향이라고 가정한다.

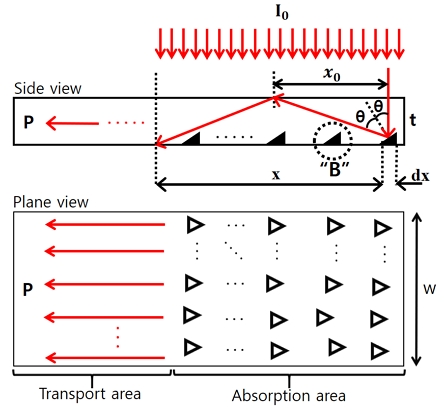
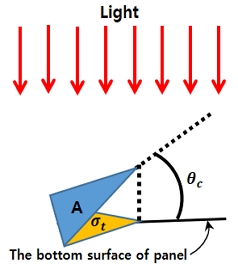
패널의 폭을 W 라 하고 패턴이 가공된 패널의 측면에서 본 조사 모습과 평면에서 본 수광부(absorption area) 및 전송부(transport area)를 Fig. 3과 같이 나타내기로 한다. 입사된 빛이 입사면 및 직각 삼각뿔 형상들의 음각된 면이 지닌 매질과 공기의 굴절률 차이에 의하여 전반사되는 것을 패널의 측면에 나타내었다. Fig. 4는 Fig. 3의 측면에서 본 하나의 직각 삼각뿔을 조사 빛에 수직한 입체 모양으로 나타낸 부분 “B”이다. Fig. 4에서 θ_c는 임계각이며 A는 직각 삼각뿔 형상으로 가공된 전반사 면이다. σ_t 는 조사 빛이 임계각 θ_c에 대한 직각 삼각뿔에 투영된 밑면적이며

Fig. 3

A side and the plane view of the panel

Fig. 4

The area σt by the critical angle and the right triangle shape of enlarged “B”

식(3) 이다. 그런데, 각각 가공된 형상의 면적이 일정하지는 않으므로 이때 발생되는 오차 Δσ_t을 고려하면 σ_t는 σ_t⇒σ_t±Δσ_t 라고 할 수 있다.

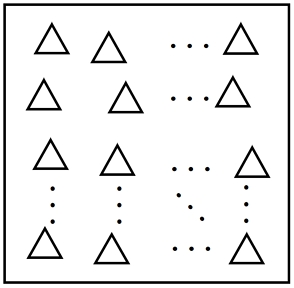
그리고 Fig. 3의 평면에서 본 수광부(absorption area)에 있는 직각 삼각뿔 형상들의 가공된 배열을 패턴이라고 한다. 패턴에는 가로와 세로의 간격이 일정한 바둑판 모양과 간격이 랜덤한 것 등이 있지만 여기서는 Fig. 5와 같이 랜덤한 것으로 한다. 이렇게 간격이 랜덤하면서 단위 면적당 균등하게 분포된 직각 삼각뿔 형상들의 개수를 패턴 밀도 ρ 라고 정한다.

Fig. 5

A plane view of pattern density ρ

전반사된 빛은 패널 내부의 위와 아랫면에서 전반사를 거듭하며 한 방향으로 전송된다. 빛의 세기 I₀가 패널에 대하여 수직인 경우, 패널의 두께 t, x₀는 빛이 수평 방향으로 진행한 거리이며, 그 길이는

식(4) 이다.

직각 삼각뿔 밑면의 반사율 γ 는 패널 바닥에 해당하는 밑면 전체의 면적 중에서 직각 삼각뿔의 투영된 밑면적이 차지하는 비율에 따라 결정되므로 반사율 γ는

식(5) 이다.

조사되는 빛의 세기 I₀, 빛이 통과하는 미소 길이 dx, 전송되는 미소 에너지 dP, 전송되는 빛이 거리 x를 통과하는 동안 바닥 면에서 몇 번 반사되는지에 따라 전송량이 결정되므로 전송되는 미소 에너지 dP는 반사율 γ에 대한 승수로 식(6)과 같이 나타낼 수 있다.

여기서 양변을 적분하여 계산하면 전송되는 에너지 P는

식(7) 이다.

한편, 아크릴에 가공된 전반사 면에 의한 반사율을 β라 하면 β는 100%가 아닌 예를 들어, β = 90 ± Δβ이라 할 수 있다. 따라서 이 경우 전송되는 에너지 P는

식(8) 로 표현될 수 있다. 그리고 여러 변수에 대한 오차들로 이루어진 오차의 전파(propagation of error)를 함수로 나타내면,

식(9) 이다.

2.3 패턴 밀도에 따른 전송 에너지 변화 고찰

선행 기초 연구에서^[6] 패널에 음각으로 가공되는 직각 삼각뿔 형상의 밑면적 σ_t와 관련된 삼각형 밑변 크기와 전송 조도에 관하여 고찰했으므로 여기서는 식(7)로부터 단위 면적당 직각 삼각뿔 형상의 개수인 패턴 밀도 ρ에 따른 전송 에너지 P의 변화에 관하여 고찰한다. 즉, 광전송 에너지 식(7) 결과 값들에 영향을 미치는 대표적인 변수로는 패턴 밀도(ρ)와 선행 기초 연구로부터^[6] 직각 삼각뿔 형상의 밑면적(σ_t)을 들 수 있다.

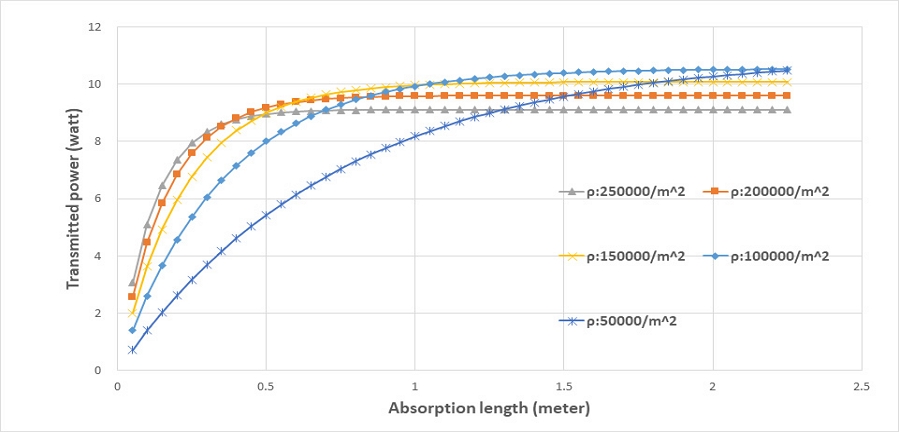
조사되는 광의 세기 I₀는 W/m²의 단위를 가지며, 입사하는빛의 단위 시간당 단위 면적당 복사 에너지로 정의되고 표준시험조건(standard test condition, Air Mass 1.5, 온도 25℃기준)의 태양광 스펙트럼 조사 강도(irradiance)로서 I₀ = 1,000 W/m²이다. 직각 삼각뿔 형상의 밑변과 높이를 각각 2 mm로 하면 직각 삼각뿔의 투영된 밑면적 σ_t는 σ_t ≃ 0.0000015 m²이고, 패널의 두께 t = 0.003 m, 가로 폭 W = 0.2 m 일때, 수광부 세로 길이 x가 0에서 2.25 m까지, 패턴 밀도 ρ을 50,000/m² 부터 250,000/m²까지 50,000/m² 단위로 계산하여 Fig. 6 그래프에 결과를 비교하여 나타냈다.

Fig. 6

Transmitted light power as a function of absorption length and pattern density

x≃0.3 m까지는 패턴 밀도 ρ = 250,000/m² 일 때 전송 에너지가 가장 높고, x≃1 m 이후부터는 패턴 밀도 ρ = 100,000/m² 일 때 전송 에너지가 가장 높은 것으로 나타난다. 즉, 패턴 밀도 ρ가 클수록 전송 에너지가 더 빨리 포화되는 것이다. 다시 말해서, 패턴 밀도가 높을수록 태양광을 급격하게 전반사 시키지만, 패널 내부에서 전송되는 빛을 가로막게 되어 세로 길이가 증가하면 측정부에서의 전송 에너지는 오히려 더 작아진다. 이렇게 단위 면적당 직각 삼각뿔 형상의 개수인 패턴 밀도 ρ 에 따라 전송 에너지가 변화되는 것으로부터 패턴 밀도를 필요에 맞게 고려함으로써 경제적이고 효율적인 태양광 전송패널이 제작될 수 있다^[7].

3.1 광전송 아크릴 패널 제작

아크릴은 투명하고 가공성이 좋으며 광학적 특성이 유리와 같이 우수하므로 기초 연구에서처럼^[6] 반사율 6.88%, 흡수율 0.12%, 투과율 93% 인 아크릴 재질로 태양광 전송패널을 제작하였다.

두께 t가 0.3 cm, 가로 폭 W는 20 cm, 전체 세로 길이 L은 45 cm 이다. 여기서 빛을 받는 패널의 수광부 세로 길이 x는 18 cm이므로 Fig. 6에 의해 x = 0.18 m에서 ρ = 250,000/m²로서 패턴 밀도가 25/cm² 이고 σ_t ≃ 0.015 cm²일 때 에너지 전송이 가장 좋다. 그러나, 실제로 cm²에 25개를 가공하기는 매우 어려우므로 여기서는 직각 삼각뿔의 투영된 밑면적 σ_t ≃ 0.01cm²로 하였으며, ρ = 100,000/m²을 기준으로 하여 ρ ≃ 10.8/cm²으로 했다. 앞서 제작된 패턴 가공 제어 장치^[8]로 Fig. 7 사진과 같이 수광부 360 cm² (20×18 cm) 내에 약 3,900개를 랜덤하게 가공하였다.

Fig. 7

An enlarged photo of the light transmission panel produced

3.2 실험 장치

Fig. 8은 광전송된 에너지를 측정하기 위한 실험 장치이다. 입사광 I₀는 I₀≃40 mW/cm²이며, 565~590 nm 파장의 노란색 단일광으로 하였고, 이것의 조도는 9,260 lx 이다. 광검출기는 Hamamatsu 사(社)의 Si Photodiode S1336-5BQ와 Testo 사(社)의 TESTO- 540을 사용했다. S1336-5BQ의 Spectral response는 580 nm에서 Photosensitivity가 약 0.3A/W이고, TESTO-540의 측정 범위는 0~99,999 lx 이며 분해능은 1lx 이다.

Fig. 8

Experimental equipment

3.3 실험 방법 및 결과 고찰

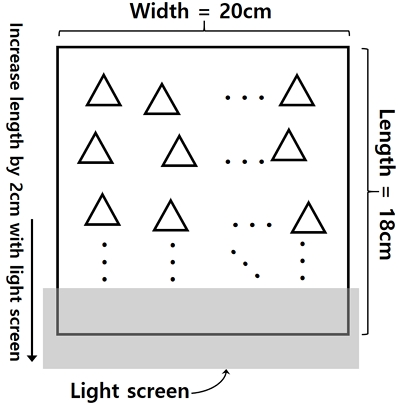
먼저, 아크릴 패널의 패턴 가공면을 밑면으로 하고 패널 윗면에 수직 입사광을 조사한다. Fig. 9와 같이 수광부의 가로 폭 W는 20 cm로 일정하게 하고 빛을 완전히 차단하는 빛 가림막을 사용하여 세로 길이 x가 2 cm부터 18 cm까지 2 cm 단위로 빛을 받는 면적을 두 배씩 증가시키면, 빛이 패널 내에서 반사되고 굴절되어 전송되므로 그 전송량을 광검출기로 측정한다.

Fig. 9

Experiment of light transmission panel by a light screen

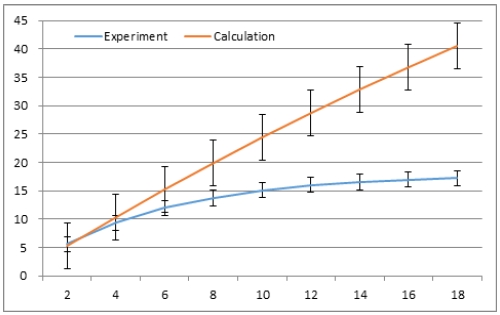
제작된 패널의 광전송 에너지를 엑셀(Microsoft excel)을 사용하여 이론적으로 계산한 결과와 실험적으로 측정한 결과를 Table 1에 비교하여 나타내었고, Fig. 10은 두 결과를 표준 오차(standard error)를 이용하여 나타낸 추론적 오차막대 그래프이다.

Table 1

Transmitted power results of calculation and experiment

Fig. 10

Error bar graph of the results

처음 세로 길이 x = 2 cm에서는 5.26 mW와 5.55 mW로서 두 결과가 거의 비슷한데 이것은 제작된 패널의 광전송을 이론식으로 예측할 수 있음을 보여준다. 그 후 차이가 점차 증가하여 x = 18 cm일 때 40.5 mW와 17.2 mW로서 약 2.3배의 차이를 보였다. 이렇게 결과에 차이가 나는 것은 제작된 패널에 비선형적인 전송 손실이 있음을 의미한다. 손실이 발생한 이유는 패널 양옆 측면으로의 빛의 산란에 의한 손실과 패널 표면에 존재하는 스크래치에 의한 손실, 백색광 잡음 등 측정 실험 환경으로부터 발생되는 것 등이 원인으로 생각된다. 그리고 패널에 음각으로 직각 삼각뿔 가공시 밑변 크기가 2 mm일 때 가장 크게 광전송^[6]되는데 여기서는 Fig. 11 과 같이 직각 삼각뿔의 밑변 크기(A)가 일정하게 가공되지 못하고 1.4 mm이하로 불균일하게 가공되어 전반사가 충분히 일어나지 못하게 된 것도 전송 손실의 원인으로 사료된다.

Fig. 11

Photo of the fabricated pattern (length A is 1.4 mm)

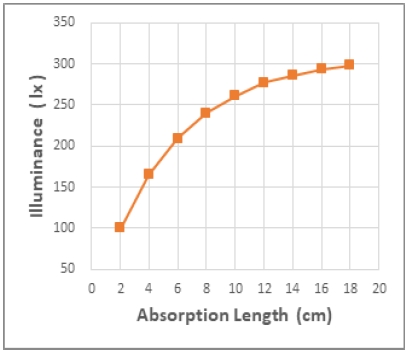
다음으로 광전송 조도가 얼마나 되며, 그것이 KS 조도 기준의 어디에 해당하는지를 확인하기 위해 TESTO-540 조도계로 광전송을 측정하여 Fig. 12에 그래프로 나타냈다. 세로 길이 x가 x = 18 cm일 때 광전송은 298 lx로서 조도 기준(KS A 3011)에서 공간의 전반 조명 방법 이상의 일반적인 작업면 조명 F에 해당하며, 입력 조도 9,260 lx 대비 약 3%에 해당한다.

Fig. 12

Transmitted light intensity was measured with a TESTO-540 illuminance meter