[ Article ]

Journal of the Korean Society of Manufacturing Technology Engineers - Vol. 32, No. 6, pp.374-380

ISSN: 2508-5107 (Online)

Print publication date 15 Dec 2023

Received 17 Oct 2023 Revised 07 Nov 2023 Accepted 13 Nov 2023

DOI: https://doi.org/10.7735/ksmte.2023.32.6.374

위상최적화를 적용한 공작기계 베드의 리브구조 최적설계와 실험적 검증

황지상^a ; 김성재^a^{, *} ; 윤정현^a ; 성철훈^b

Optimal Design and Experimental Validation of the Rib Structure of a Manufacturing Machine Bed Using Topology Optimization

Ji-Sang Hwang^a ; Sung-Jae Kim^a^{, *} ; Jeong-Hyun Yoon^a ; Chul-Hoon Sung^b

aDepartment of Mechanical Engineering, Graduate school of Dong-A University
bInstitute of Technology, Sungsan Amdeco Inc.

Correspondence to: ^*Tel.: +82-51-200-7647 E-mail address: sjkim641@dau.ac.kr (Sung-Jae Kim).

Abstract

As the eco-friendly automotive industry grows, interest in machinery research for producing environmentally friendly vehicle components increases. Among the components of a manufacturing machine, high stiffness is essential for the bed of the frame. Currently, rib design relies on the experience of mechanical engineers; thus, establishing an optimal method for rib structure design is crucial. This study employed topology optimization to derive the rib structure of the bed. Following this optimization, a compression test was conducted on test specimens from both the initial and optimized designs, produced using a 3D printer. This research confirmed the applicability and validity of using topology optimization in rib structure optimization.

Keywords:

Rib, Machine tool, Static stiffness, Lightweight, Structural analysis, Topology optimization

1. 서 론

최근 전기자동차 및 수소차 등의 친환경차 시장이 부상하고 있다. 친환경차를 구성하는 부품들은 안전을 유지하기 위해 높은 정밀도가 요구된다. 따라서 이를 위한 공작기계의 연구가 집중되고 있다. 공작기계는 크게 주축, 안내면, 프레임으로 구성되어 있다. 이중 베드는 프레임에 해당되어 중심축이나 구조물을 지탱하고 안정성을 제공하는 역할을 하며, 일반적으로 테이블 등을 안내하는 안내면을 구비하고 있다. 베드는 특정 작업을 수행하기 위해 다양한 부속품과 도구가 부착되는 곳이며, 이러한 장비들의 자중과, 공작물의 중량 등에 의해서 변형되는 특성을 가진다. 발생한 변위는 가공 정밀도의 저하와 연관되므로 강성확보를 위한 설계가 이루어져야 한다. 일반적으로 강성을 높이기 위하여 제품의 두께를 두껍게 설계하거나, 리브를 설치하는 방법이 있다. 여기서 리브를 설치하는 것이 관성모멘트를 증가시켜 강성을 높일 수 있으므로 제품을 두껍게 하는 것보다 좋다. 하지만 과도하게 리브를 설치할 경우에는 부품의 수축을 발생시키고 재료를 많이 사용함에 따라 경제적 측면에서도 불이익이 발생한다. 게다가 공작기계의 리브 설계가 설계자의 경험에 의존되어^[1] 구조 강성에 영향을 미치는 문제가 발생하기 때문에 리브의 최적 설계가 필요하다. 최적 설계에는 설계 변수에 따라 치수 최적화, 형상 최적화, 위상 최적화로 구분된다. 치수 최적화 사례로 Han 등^[2]은 내륜 볼 트랙 전용 정밀 연삭기 베드의 설계 변수인 17개 리브의 두께에 대하여, 직교 배열표를 이용한 실험 계획법과 단계적 회귀 분석을 통해 각각 목적함수에 대한 반응 표면 모델로부터 최적점을 찾아낸 바 있다. 위상 최적화를 활용한 사례로 Kim 등^[3]은 고정식 해양구조물에 대하여 위상 최적화 활용하여 최적 설계안을 도출하였다. 그리고 3D 프린트로 제작한 시험편으로 압축 시험을 수행함으로써 설계를 검증한 바 있다. 또한 Park 등^[4]은 자동차 현가장치 부품 중에서 로어 컨트롤 암을 위상 최적화하였으며, 3D 프린트의 적층 방향에 따른 시험편을 제작하여 인장 시험을 통한 실험적 검증을 수행한 바 있다. 상기한 연구들을 살펴보면 베드의 리브에 대하여 치수 최적화를 하거나, 위상 최적화 기법을 활용하여 구조물을 최적화하고 구조 시험을 실시하였다. 이외의 위상 최적화 연구에서는 비교적 작은 기계부품에 대하여 최적 설계를 수행한 사례^[5-9]를 다수 찾아볼 수 있다. 마지막으로 위상 최적화 기법을 활용하여 칼럼의 리브를 최적 설계하는 선행연구^[10]를 수행한 바 있다. 그러나 압축 하중을 받는 베드의 리브 구조를 직접적으로 설계 변경하고 구조 시험을 통해 실험적 검증을 수행한 사례는 찾아보기 어렵다.

본 연구에서는 위상 최적화 기법을 활용하여 공작기계 베드의 리브 구조를 최적 설계하였다. 이를 통해서 리브 구조 설계에 위상 최적화 기법의 적용 가능성을 확인하고자 하였다. 최적 설계를 진행하기 앞서 상용 유한 요소 프로그램인 ANSYS Workbench를 사용하여 강성 해석을 수행하였다. 그리고 위상 최적화 기법을 도입하여 최적의 리브 구조를 도출하였다. 또한 3D 프린팅 기술을 통해서 시험편을 제작하였으며, 압축 시험기를 활용하여 구조 시험을 진행함으로써 설계 검증을 실시하였다.

2. 위상최적화

2.1 밀도 함수법

위상 최적화(topology optimization)는 주어진 형상의 최적 배치를 결정하는데 관심이 있다. 공간의 어떤 지점에 요소가 배치되어야 하고 어떤 지점이 공백으로 남아 있어야 하는지 결정해야 한다. 즉, 위상 최적화는 하중 및 경계조건을 제약조건에 만족시키기 위해서 설계 공간의 질량을 재분배하는 기법이다. 대표적으로 균질화법(homogenization metod), 밀도 함수법(density function method)이 있다. 밀도 함수법은 유한 요소 해석 프로그램인 Ansys에서 일반적으로 사용되는 기법이다. 이는 Mlejnek와 Schirrmacher^[11]이 제안한 방법으로써 물질의 밀도의 분포를 고려하고 구조물의 요소(elemnt)들을 제어하여 최적의 형상을 도출한다.

일반적으로 최적 설계는 목적 함수(objective function)의 컴플라이언스(compliance)를 최소화한다. 이는 값이 작을수록 구조물의 전역 강성(global stiffness)이 커지게 되어, 구조물은 더 견고하고 안정적인 상태가 된다. 이러한 컴플라이언스를 수식으로 나타내면 다음 식 (1)^[12]과 같다.

C o m p l i a n c e = ∫ V f u d V + ∫ S t u d S + ∑ e N F e u e

(1)

여기서 u는 변위장, f는 물체에 전체적으로 분포하는 힘, F_e 는 e번째 노드에 가해지는 하중, u_e는 e번째 변위 자유도, t는 견인력, S는 연속체의 표면적, V는 연속체의 부피를 뜻한다. 여기서 컴플라이언스를 최소화하기 위한 대부분의 일반적인 최적화 문제는 식 (2)^[13]와 같이 표현된다.

Minimize C ρ e = F T u

(2)

K u = F

(3)

위 식에서 C는 컴플라이언스 함수, u는 변위벡터, F는 하중 벡터, K는 강성 매트릭스이다. 여기서 밀도 함수법을 식 (2)와 (3)으로부터 FEM 형태의 식으로 표현하면 다음 식 (4)^[13]와 같이 정식화할 수 있다.

Minimize C ρ e = u T K u = ∑ e = 1 N ρ e p u e T K e u e Subject to ∑ e = 1 N v e ρ e ≤ V 0 < ρ m i n ≤ ρ e ≤ 1, e = 1,2, 3 … N

(4)

위 식에서 ρ는 유사밀도(pseudo density), p는 벌칙인자 또는 페널티 계수(penalty factor), V는 설계 공간의 부피이다. 여기서 유사 밀도 ρ가 0인 경우에는 요소가 공백(void)으로 간주되어 요소가 비 활성화되고 1인 경우에는 요소가 활성화되며 최적화가 이루어진다. 이러한 방법으로 유사밀도의 분포가 구해지면 0과 1사이의 중간 값이 명확하지 않은 설계를 생성하기 때문에 문제가 발생한다.

2.2 SIMP법

연속 함수를 사용하면서 유사 밀도의 0과 1사이의 중간 값을 보정하기 위해 SIMP(solid isotropic material with penalization) 법을 사용하여 벌칙화하게 된다. 이는 BendsØe와 Sigmund^[14]가 제안하였으며, 유한 요소 해석 프로그램에서 밀도 기반의 위상 최적화를 수행하기 위해 일반적으로 사용되는 접근법이다. 벌칙화를 위해 사용되는 매개변수를 페널티 계수라 하며, 페널티 계수는 식 (5)^[13]에서 유사 밀도와 탄성계수와의 상관관계식으로부터 정의된다.

E E o = ρ p, p > 1

(5)

위의 식 (5)에서 E는 등가 탄성계수, E_o는 재료의 탄성계수이다. 페널티 계수로 인하여 밀도와 탄성계수의 관계에서 비선형을 만들게 되며, 일반적으로 2에서 4의 값을 사용하고 있다. 여기서 페널티 계수가 2일 경우에는 비선형성이 작아 유사밀도의 중간 값이 많이 나온다. 그리고 4일 경우에는 비선형 곡선이 급격히 변화하므로 최적화 결과가 매끄럽지 못하는 경향이 있다. 때문에 페널티 계수는 주로 3을 사용하여 보정하게 된다.

3. 베드의 리브구조 최적설계

3.1 초기 설계안의 정강성 해석

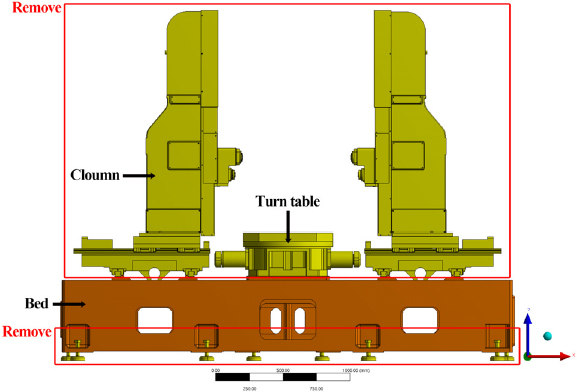
베드는 Fig. 1과 같이 두 개의 칼럼과 턴테이블을 지지하고 있다. 이때 칼럼은 베드의 안내면을 따라서 Y축 방향으로 작동한다. 따라서 안내면에 주요부의 중량을 고려하여 하중을 적용해야 한다. 우선 구조 해석을 수행하기 앞서 Fig. 1과 같이 해석 대상물을 간소화하였다. 그리고 베드와 결합되는 주요부의 중량을 고려하여 하중을 적용하였다. 칼럼이 설치되는 안내면에 각각 11376 N, 턴테이블이 설치되는 지점에는 6383.2 N을 적용하였다. 이어서 자중을 고려하여 중력 조건을 추가하였으며, 베드의 발판을 구속 조건으로 적용하였다. 사용 소재는 FC30이며, 물성치는 Table 1과 같다.

Fig. 1

Simplified bed shape

Table 1

Material property

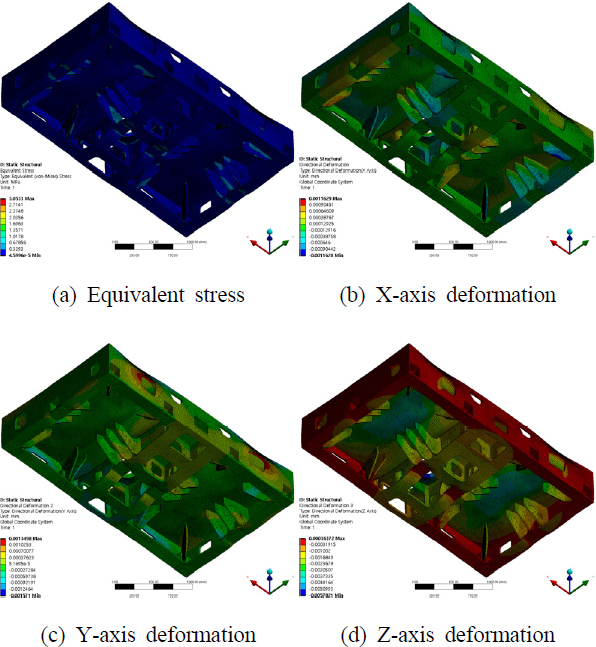
강성 해석 결과 Fig. 2에 도시한 바와 같이 최대 응력은 5.4778 MPa로 도출되었다. 이는 안전율이 41.5에 달하는 수치이다. 또한 각 축의 변형량은 X축이 2.878μm, Y축 2.67μm, Z축 12.942 μm이다. 여기서 베드는 Z축 방향으로만 하중이 가해졌으므로 Z축 강성을 도출하면 878.99 N/μm이다. 결과를 종합해 보면 초기 설계안은 상대적으로 높은 안전율과 강성을 가지고 있다. Fig. 2를 살펴보면 Z축 하중으로 인하여 외곽의 리브에 응력과 변형이 집중적으로 발생하는 것을 확인할 수 있다. 이는 외곽의 리브 구조가 베드의 강성에 크게 기여하고 있으나 중심부의 리브는 그렇지 못하다는 것을 의미한다. 베드의 강성이 우수하더라도 불필요한 리브의 배치로 인하여 비용이 증가하므로 리브 구조에 대한 최적화 및 경량화 연구가 필요하다.

Fig. 2

Analysis result of initial shape

Fig. 3

Optimization area

3.2 최적설계 제약조건

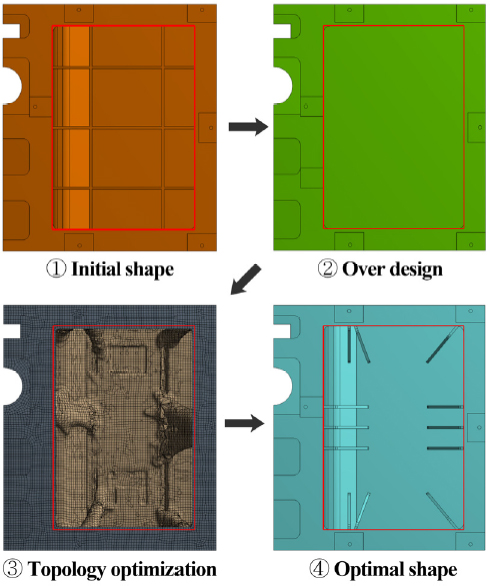
초기 설계안은 직교 리브 구조로 설계되어 있으며, 베드는 좌우 형상이 대칭구조이다. 따라서 위상 최적화 시 시간을 절약하고자 형상을 반으로 분할하고 대칭 조건을 부여하였다. 다음으로 리브가 배치되지 않은 초기 설계 단계의 형상이 필요하므로 Fig. 4-2와 같이 오버 디자인(over design)을 하였다. 다음으로 식 (6)과 같이 목적함수와 제약조건을 정의하였다.

Fig. 4

Rib optimization process

Minimize compliance Subject to displacement ≤ 18.11 μ m M a s s < 2061.9 k g

(6)

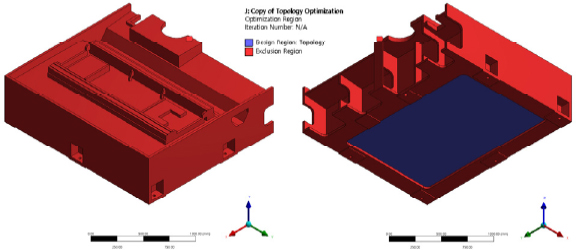
초기 설계안의 질량은 4123.8kg 이다. 따라서 제약조건은 분할된 형상의 질량인 2061.9kg 미만이 되도록 하였다. 또한 초기 설계안의 최대 변형량인 18.11µm 이하가 되도록 하였다. 페널티 계수는 수렴성을 고려하여 3으로 설정하였으며, 설계 영역은 Fig. 3과 같이 초기 리브가 설계되어 있던 베드의 하면으로 지정하였다.

3.3 위상최적설계 결과

이와 같은 조건으로 최적 설계를 수행한 결과 Fig. 4-3과 같이 초기의 직교 리브 구조가 아닌, 발판과 안내면의 설치지점까지 연결된 형상이 생성되었다. 이는 초기 설계안의 리브 구조와 달리 중심부를 지나는 리브의 배치가 부적절하다는 것을 보여준다. 이러한 결과를 바탕으로 Fig. 4-4와 같이 리브를 설계하였다. 이때 베드의 리브 치수는 초기 두께 20mm, 높이 397.6mm를 기준으로 설계하였다.

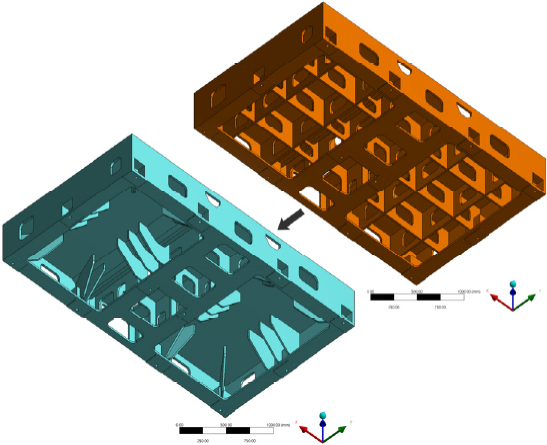
최적 설계 후 질량의 변화를 비교한 결과 Table 2에 도시한 바와 같이 초기 질량 4123.8kg에서 최적화 후 3926.6kg으로 4.78% 경량화되었으며, 최적화 전·후의 설계안은 Fig. 5에 도시하였다.

Table 2

Mass change after topology optimization

Fig. 5

Optimized shape of bed

3.4 최적 설계안의 설계 평가

최적 설계의 검증을 위해서 최적 설계안에 대해 초기 설계안과 같은 조건으로 정강성 해석을 수행하였다. 그 결과 Fig. 6과 Table 3에 도시한 바와 같이 최대 응력과 3축의 변형량을 도출하였다. 베드의 최대 응력은 3.053 MPa이며 초기 형상 대비 44.3% 감소하였다. 그리고 X축은 1.163 µm로 59.6% 감소, Y축은 1.581 µm로 41.7% 감소, Z축은 5.782 µm로 55.3% 감소하였다. 리브 최적 설계로 인하여 Z축의 처짐이 감소함에 따라 X, Y축의 변위가 감소되었다. 이는 Z축 변위가 X, Y축의 변위에도 영향을 준다는 것을 보여준다. 그리고 Z축의 강성을 도출한 결과 1967.49 N/µm로 기존 대비 123.84% 증가하였다. Z축 하중을 받는 베드의 리브 구조에 위상 최적화 기법을 적용함으로써, 3축의 변형량이 감소하였다. 따라서 Z축 하중이 형상의 변위에 큰 영향을 미치는 것을 확인하였으므로 압축 시험을 통한 설계 검증이 필요하다.

Fig. 6

Analysis result of optimized shape

Table 3

Comparison of analysis result after optimization

4. 압축시험을 통한 설계 검증

4.1 3D프린터의 시험편 물성 조건

본 실험의 시험편을 제작하기 위해서 사용된 장비는 FDM 방식의 3D 프린터이다. 압축 시험을 통해서 구조물의 강성 변화를 정량적으로 파악하고자 한다면, 소재의 물리적 및 기계적 특성이 일치해야 한다. 하지만 시험편 제작 시 사용된 재료는 실제 구조물의 재료인 FC30이 아니라 ABS 소재가 사용되었다. 이러한 경우 두 소재의 강도, 탄성계수, 파괴 거동 등의 물성치가 상당히 달라 정량적인 결과 값을 얻기 힘들다. ABS 시험편은 FC30과 비교했을 때 보다 낮은 강도와 탄성계수를 가지므로 압축 시험 시 상대적으로 취약하다. 또한 적층 방식으로 인하여 시험편의 내부 구조에 결함이 발생하여 시험에 영향을 미칠 수 있다. 하지만 본 실험의 목적은 위상 최적화 기법을 통해 설계된 리브 구조의 배치에 따라 베드의 강성이 긍정적으로 변화되는 여부를 확인하고 경향성을 파악하는 것이다. 따라서 최적 설계 전과 후의 시험편이 같은 조건으로 제작되고 리브의 구조만 다를 때 압축 시험의 결과 그래프의 하중-변형 곡선을 분석함으로써 정성적인 설계 검증이 가능하다.

4.2 압축 시험편 제작

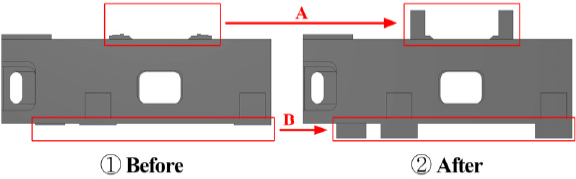
압축 시험 시 힘이 작용하지 않는 지점에 하중이 발생하고 시험 중에 리브가 아래로 변형하며 바닥에 닿아 시험 결과에 영향을 미치는 문제가 발생할 수 있다. 이러한 이유로 실제로 하중이 작용하는 지점을 구분하고 리브와 바닥의 간격을 늘려줄 필요가 있었다. 따라서 Fig. 7의 A와 같이 베드에서 하중이 작용하는 안내면에 150 mm의 기둥을 세워 올렸으며, B와 같이 발판의 높이를 80 mm 증가시켰다. 그 후 3D 프린트를 사용하여 실측의 0.033배 크기로 초기 및 최적 설계안 시험편을 제작하였다. 이때 출력 품질을 향상시키기 위해서 밀도는 100%, 레이어 높이는 0.1 mm, 벽 라인은 5개로 하여 Fig. 8과 같이 시험편을 제작하였다.

Fig. 7

Change in design of test specimen

Fig. 8

Test specimen produced by 3D printing

4.3 베드의 압축 실험

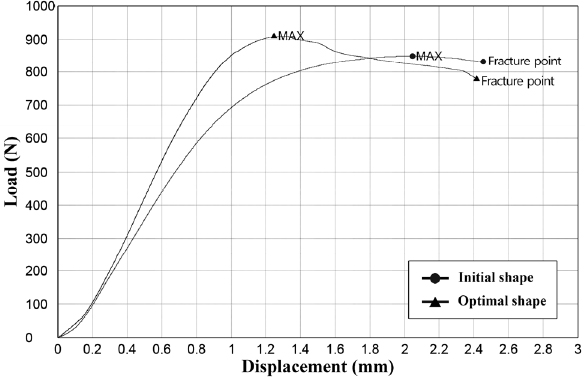
실험에 사용된 장비는 SHIMADZU 사의 10 ton 급 압축시험기이며, Fig. 9와 같이 베드의 초기 및 최적 설계안에 대한 압축 실험을 진행하였다. 압축 시험의 속도는 1 mm/min로 운용되었으며, 시험편의 파단이 일어날 때까지 수행하였다. 압축 시험 결과는 Fig. 10의 하중-변위 선도를 통해서 나타내었다. 그리고 복잡한 형상의 베드는 압축시험을 통해 응력 및 X, Y축의 변위를 관찰하기 어려움으로 변형에 가장 큰 영향을 미치는 Z축 변위의 관점에서 분석하였다. 압축 시험 결과 그래프에서 초기 설계안의 최대 하중은 849 N이며, 최적 설계안의 최대 하중은 911 N이므로 최적 설계를 통해 강도가 증가된 것을 확인할 수 있다. 그리고 초기 설계안의 최대 하중을 최적 설계안과 동일한 하중에서 변위를 비교하였을 때, 최적 설계안의 변위는 약 2 mm에서 약 1 mm로 최대 50% 감소되는 것을 볼 수 있다. 또한 실험 그래프의 선형 기울기로부터 강성을 도출한 결과 초기 설계안은 0.733 N/µm이며, 최적 설계안은 0.833 N/µm이므로 최적 설계 후 강성이 증가되는 경향을 보여준다. 따라서 본 실험을 통해 위상 최적화 기법을 적용한 설계안이 초기 설계안에 비해서 강성과 강도가 개선되는 것을 확인할 수 있었다.

Fig. 9

Compression test of bed

Fig. 10

Force-displacement curves of bed

5. 결 론

본 연구에서는 위상 최적화 기법을 활용하여 공작기계 베드의 리브 구조를 최적 설계하였다. 그리고 3D 프린트를 사용하여 초기 및 최적 설계안의 시험편을 제작하고 압축 시험을 수행하여 결과를 비교분석하였다. 이와 같은 연구로 위상 최적화를 통한 리브 구조 도출의 적용 타당성을 확인하였다.

위상 최적화를 수행하여 도출된 최적 설계안의 최대 응력은 3.053 MPa으로 초기 설계안 대비 44.3% 감소하였다. 그리고 X축의 변위는 1.163 µm로 59.6% 감소하고 Y축 변위 1.581 µm로 41.7% 감소, Z축 변위는 5.782 µm로 55.3% 감소하였다. 이를 통해서 압축 하중에 대한 Z축 강성이 1967.49 N/µm로 123.84% 증가하였다. 그리고 질량이 4123.8 kg에서 3926.6 kg으로 감소하여, 약 4.78% 경량화되었다. 다음으로 압축시험으로부터 최적 설계안의 리브 구조 강성이 더 크다는 것을 검증하였다. 실험 결과로부터 강성을 도출한 결과 초기 설계안은 0.733N/µm 이며, 최적 설계안은 0.833 N/µm 이다. 그리고 최대 하중은 849 N에서 911 N으로 증가하였다. 게다가 초기 설계안의 최대 하중과 동일한 하중에서 최적 설계안을 비교하면 변위는 약 2 mm 에서 약 1 mm로 최대 50% 감소하는 것을 볼 수 있다. Table 3에서 Z축 하중의 변위가 55.3% 감소한 것을 비교해 보면 근사한 수치이다. 따라서 본 연구를 통해서 베드의 리브 구조에 위상 최적화 기법을 적용하면 강성과 강도를 개선할 수 있다는 것을 확인할 수 있었다.

이러한 결과는 리브 구조를 도출할 때 위상 최적화 기법이 치수 최적화 기법보다 우수하다고 생각된다. 일반적으로 치수 최적 설계에서는 리브의 두께를 설계 변수로 하여 최적 설계를 진행하므로 새로운 리브 구조를 도출하기는 어렵다. 하지만 위상 최적화 기법을 사용한다면 재료가 필요한 영역을 재배치하여 이를 직관적으로 표현해 주기 때문에 리브 배치를 쉽게 고려할 수 있어 강성 확보와 경량화에 도움을 준다는 것을 보여준다. 따라서 위상 최적화 기법은 초기 설계 단계에서 리브 구조 설계에 적용하는 것이 타당하다고 판단된다.

다만, 결과를 토대로 리브를 배치하는 것 또한 설계자의 역량이 필요하다. 위상 최적화 결과에서 재료가 집중된 곳에 대하여 설계자가 리브를 배치할 때 개수 및 두께 등에 따라 구조 강성과 질량이 변화하기 때문에 최적 설계 과정에서 여러 번의 시행착오를 겪을 수 있다. 그러나 위상 최적화 기법을 공작기계 산업에서 베드의 개념설계 단계에 적용한다면 리브 구조 설계에 대한 방향을 합리적으로 제시하고 설계 시간 또한 단축시킬 수 있을 것이라 사료된다.

References

Chung, J., Lee, K., 1996, Optimal Topology Design of Structures and Ribs Using Density Distribution, J. Korean Soc. Precis. Eng., 13:7 66-77.
Han, H. W., Han S. H., 2020, Optimal Shape Design of Supported Structure for Inner Race Track Grinding Machine, Trans. Korean Soc. Mech. Eng. A, 44:3 221-227. [https://doi.org/10.3795/KSME-A.2020.44.3.221]
Kim, H.-S., Kim, H.-S., Park, B., Lee, K., 2020, 3D Topology Optimization of Fixed Offshore Structure and Experimental Validation, J. Ocean Eng. Technol., 34:4 263-271. [https://doi.org/10.26748/KSOE.2019.052]
Park, H.-M., Lee, G.-B., Kim, J., Seon, C.-R., Yoon, M., 2022, Experimental Validation of Topology Design Optimization Considering Lamination Direction of Three-dimensional Printing, Journal of the Computational Structural Engineering Institute of Korea, 35:3 191-196. [https://doi.org/10.7734/COSEIK.2022.35.3.191]
Im, J. M., Kim, J. Y., Shin, K. B., Kim, D. Y., 2018, Lightweight Design of Link Structures for Amphibious Boat using Topology Optimization Method, J. Korean Soc. Precis. Eng., 35:11 1085-1092. [https://doi.org/10.7736/KSPE.2018.35.11.1085]
Cho, Y., Yoon, W., 2020, Optimal Design for Strength Improvement of Support Bracket for Sanding Device of Railway Vehicle Using Topology Optimization, J. Korean Soc. Precis. Eng., 37:4 263-270. [https://doi.org/10.7736/JKSPE.019.114]
Shi, G., Guan, C., Quan, D., Wu, D., Tang, L., Gao, T., 2020, An Aerospace Bracket Designed by Thermo-elastic Topology Optimization and Manufactured by Additive Manufacturing, Chin. J. Aeronaut., 33:4 1252-1259. [https://doi.org/10.1016/j.cja.2019.09.006]
Sarode, R. B., Sarawade, S. S., 2017, Topology Optimization of Excavator Bucket Link, Proc. 6th National Conference (RDME 2017), 12-26. [https://doi.org/10.9790/1684-17010051226]
Chen, Y., Wang, Q., Wang, C., Gong, P., Shi, Y., Yu, Y., Liu, Z., 2021, Topology Optimization Design and Experimental Research of a 3D-Printed Metal Aerospace Bracket Considering Fatigue Performance, Appl. Sci., 11:15 6671. [https://doi.org/10.3390/app11156671]
Hwang, J.-S., Kim, S.-J., Sung, C.-H., 2023, Study on the Optimal Design of Column Rib Structure of Horizontal Machine Tool Using Topology Optimization Technique, J. Korean Soc. Manuf. Technol. Eng., 32:1 1-7. [https://doi.org/10.7735/ksmte.2022.32.1.1]
Mlejnek, H. P., Schirrmacher, R., 1993, An Engineer's Approach to Optimal Material Distribution and Shape Finding, Comput. Meth. Appl. Mech. Eng., 106:1-2 1-26. [https://doi.org/10.1016/0045-7825(93)90182-W]
Tamta, S., Saxena, R., 2016, Topological Optimization of Continuum Structures Using Optimality Criterion in ANSYS, International Research, International Research Journal of Engineering and Technology, 3:7 1483-1488.
Bendsøe, M. P., Sigmund, O., 2003, Topology Optimization: Theory, Methods, and Applications, Springer Verlag, Berlin.
Bendsøe, M. P., Sigmund, O., 1999, Material Interpolation Schemes in Topology Optimization, Arch. Appl. Mech., 69 635-654. [https://doi.org/10.1007/s004190050248]