구조동역학에서 iIRS방법을 활용한 효율적인 인공신경망 접근 방안

2.1 Guyan method

Guyan method는 정적상태의 운동방정식에서 관성항을 무시할 수 있는 조건으로 노드를 비활성화시켜 차수를 감소시키는 기법이다^[5]. 정적상태의 운동방정식은 일반적으로 다음과 같이 표시할 수 있다.

정적상태 조건에서 관성 효과를 무시할 수 있으므로 강성 행렬에 관해 활성화 노드와 비활성화 노드로 분류해 정리하면 다음과 같다.

여기서 M, K, F는 각각 질량, 강성, 힘 행렬을 의미한다. u, $$ \ddot{\mathbf{u}}$$은 각각 변위와 가속도 행렬을 의미한다. 아래 첨자 n은 전체 노드 수를 의미하고 a는 활성화 노드를 d는 비활성화 노드를 의미한다. 정적상태이기 때문에 가해지는 가속도를 0으로 놓아 식 (1)을 강성만 고려한 식 (2)로 정리할 수 있다. 식 (2)의 두 번째 행에서 비활성화 노드에 대해 작용력을 0으로 놓을 수 있다.

식 (3)을 u_d에 대해 정리하면 비활성화된 노드에 대한 위상관계식을 얻을 수 있고 이에 대해 변환 행렬 T를 얻을 수 있다.

여기서 I는 단위 행렬이다. 얻어진 변환 행렬을 Guyan 축소 방법에 따라 강성 행렬과 질량 행렬에 적용하면 다음과 같이 쓸 수 있다.

Guyan method는 다중 입력 변수 환경에서 차수 감소를 가능하게 하는 방법으로 사용할 수 있지만 관성항을 모두 무시하기 때문에 정확도를 충분히 보장하지 못하는 경우가 생길 수 있다. 다음 섹션에서 이와 같은 문제를 보완한 IRS 방법에 대해 설명한다.

2.2 Improve reduced system

Improve reduced system (IRS)은 구조 동역학 분야에서 차수 감소를 위해 사용할 수 있는 방법으로 관성항을 무시하여 차수 감소에 사용했던 Guyan method를 개선하는 방법으로 관성항을 적정값으로 가정하여 근사함으로 정확도를 높일 수 있는 방법이다^[6]. 식 (2)에서 $$ {\ddot{\mathbf{u}}}_{\mathrm{a}}$$과 u_a의 관계를 정리하기 위해 다음과 같이 표현할 수 있다.

식 (1)에 앞에서 구한 식 (6)과 (7)을 적용하여 식 (8)의 활성화 노드 u_a에 대해 λ²을 $$ {-\mathbf{M}}_{\mathrm{G}\mathrm{u}\mathrm{y}\mathrm{a}\mathrm{n}}^{-1}{\mathbf{K}}_{\mathrm{G}\mathrm{u}\mathrm{y}\mathrm{a}\mathrm{n}}$$으로 가정할 수 있다.

이를 식 (4)에 대해 정리하면 다음과 같다.

식 (12)을 정리하여 다음과 같이 변환 행렬을 생성한다.

생성된 변환 행렬을 질량과 강성 행렬에 행렬곱을 하는 것으로 데이터를 축소시킬 수 있다. 다음 섹션에서는 이와 같은 방법을 반복 적용한 iIRS에 대해 설명하고자 한다.

2.3 iterated Improve Reduced System

1995년 Frisswell에 의해 IRS 방법은 반복 적용되어 정확도를 향상시킬 수 있음이 발견되었다^[7]. Frisswell의 논문에서 이 방법은 iterated Improve Reduced System (iIRS)로 명명되었다. iIRS는 식 (14)을 반복 적용하는 방법으로 다음과 같이 이전 단계의 데이터를 사용하여 더 높은 성능의 변환행렬을 구하는 기법이다.

위 식에서 i는 IRS 방법을 반복 적용한 횟수를 의미한다.

2.4 고유값 오차 비교

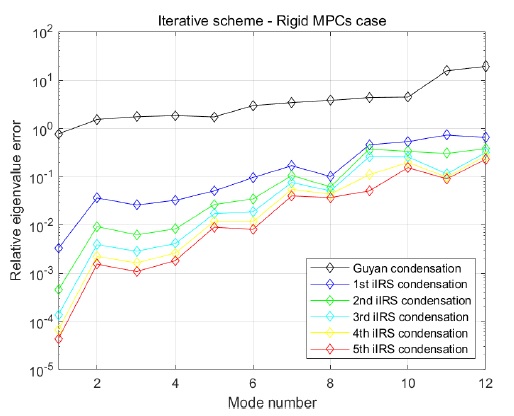
앞서 설명한 방법들의 정확성을 판단하기 위해 rigid body의 강성 행렬을 각 방법으로 압축하여 각각의 고유값 오차를 측정하였다. 압축 전의 강성 행렬은 18316의 크기를 가지고 있었으며 이를 12의 크기로 압축하였다. Fig. 1에 각 방법에 대해 압축된 12개의 모드별로 고유값 오차의 결과를 나타내었다. 상대적인 고유값 오차에 대한 식은 J.-G. Kim(2015)의 논문의 식을 사용하였다^[8].

Fig. 1

Eigenvalue error of Guyan and iterated IRS condensation

Guyan method에 비해 IRS method가 고유값을 더 잘 포함하는 것을 알 수 있으며 IRS method를 2번 적용한 2nd IRS method는 보다 더 낮은 오차를 나타내는 결과를 보였다.

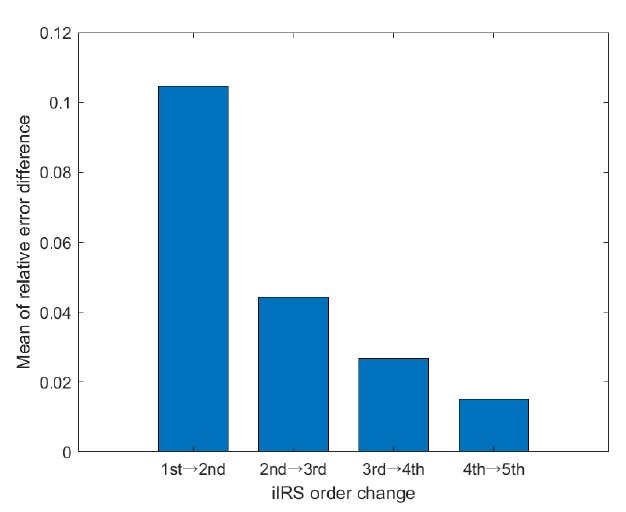
반복 횟수가 증가할수록 고유값 오차는 작아지는 결과를 보이지만 Fig. 2에 표시한 것과 같이 오차의 감소 폭 또한 반복할수록 작아지는 결과를 보였다. Friswell, M. I. (1998)의 논문을 참고하여 iIRS의 수렴 지점을 판별하였고 이 결과로 5차 iIRS를 신경망 구조에 적용하였다^[9].

Fig. 2

Mean of relative error difference according to order change

이어서 다음 장에서는 구조 동역학에서 이러한 차수 감소 모델링을 적용한 신경망 구조에 대해 설명한다.

3.1 신경망 구성

신경망의 알고리즘은 feedforward algorithm으로 구성하였다. Loss function은 MSE로 사용되며 Optimizer는 Adam을 사용하였다. 전체 데이터와 감축된 데이터의 크기가 다르기 때문에 각 모델에 데이터의 크기를 고려한 매개변수를 갖는 신경망을 생성하였다. 신경망 구조에 대한 초매개변수들은 Table 1에 정리하였다.

Table 1

Hyper parameters of proposed method

3.2 훈련 과정

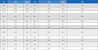
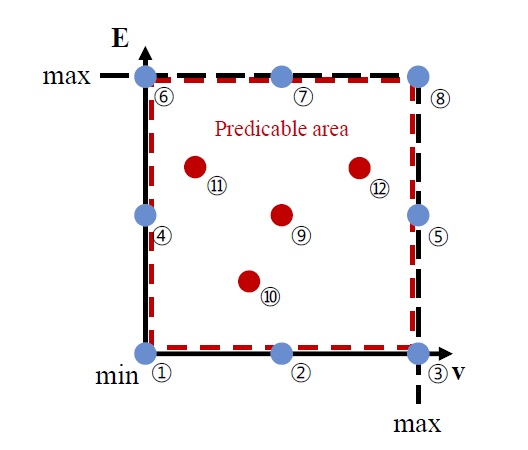
앞서 보인 iIRS를 적용하여 감축된 데이터를 신경망 구조에 학습시키는 제시된 방법을 본 논문에서 다변수 ROM-NN (reduced ordered method-neural network) 방법으로 명명하고자 한다. 다변수 ROM-NN 과정은 먼저 parameter를 선별하는 과정이 요구된다. 본 논문에서 사용한 parameter는 Al 2024-T4부터 Al 6061-T6까지의 parameter를 사용하였다. 이에 대해 Fig. 3와 같이 최대와 최소값을 설정하여, training data의 기반이 되는 training parameter는 전체 parameter domain의 경계값으로 선정하고 test data의 기반이 되는 test parameter는 parameter domain 내부에 위치하는 값으로 선정한다. 이에 따라 본 논문에서의 training parameter는 Table 2의 ①~⑧이며 test parameter는 Table 2의 ⑨~⑫이다.

Fig. 3

Classification of maximum and minimum of input data and specify predictive data

Table 2

Property parameter list of gearbox housing

Training parameter에 해당하는 조건에서 외력에 대한 변위 행렬을 구하기 위해 Newmark method를 사용하여 전체 변위 행렬을 계산한다^[10]. 계산된 전체 변위 행렬 U_1∼8는 iIRS를 통해 변환 행렬 T_1∼8를 구하고 이를 사용하여 U_1∼8을 q_1∼8로 축소시킨다. 이렇게 구한 q_1∼8는 다변수 ROM-NN 방법에서 training data로 사용한다. Test data는 test parameter에 해당하는 변위를 압축시킨 q_9∼12로 사용한다. 변환 행렬을 사용해 축소하는 과정을 아래에 식으로 나타내면 다음과 같다.

여기서 T는 변환 행렬을 의미하며 U는 전체 변위 행렬을 의미한다.

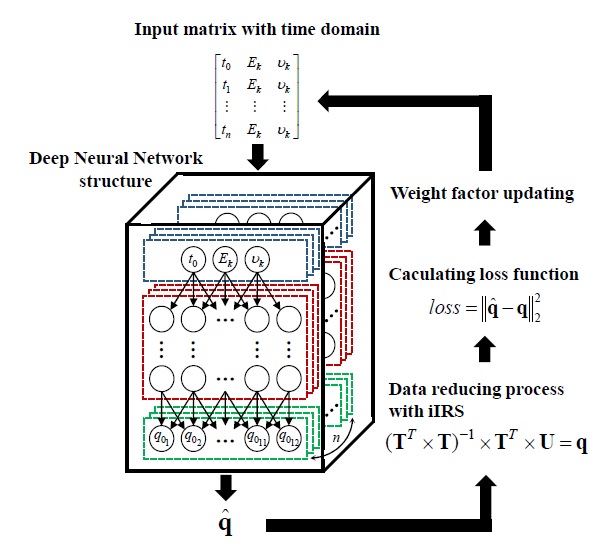
제시한 신경망에서 각 시간에 따른 input값으로 q를 예측하기 위해 Newmark method에서 적용한 시간 간격을 input으로 하는 input 행렬 X_k를 생성한다. X_k는 다음과 같이 구성한다.

여기서 t는 시간을 나타내고 n은 총 시간을 나눈 수이다. E와 ν는 각각 Young’s modulus와 Poisson ratio를 의미하며 k는 파라미터의 번호를 의미한다. 학습효율을 향상시키기 위해 데이터 전처리 과정으로 학습하는 전체 input data에 대해 batch normalization을 적용하였다^[11]. Batch normalization은 신경망의 학습률을 향상시킴과 동시에 overfitting을 방지하여 initialization에 덜 민감하게 하는 효과가 있다. 이후 생성된 신경망에 각 X_k를 input으로 학습을 진행시키고 그 결과를 training data인 q_1∼8과 비교하여 가중치를 조정한다. 그러면 신경망은 각 시간 구간과 Young’s modulus, 그리고 Poisson ratio를 입력받음으로 $$ {\widehat{\mathbf{q}}}_{1~8}$$을 도출하고 이를 반복할수록 q_1∼8과 유사해진다. 이러한 훈련 과정의 알고리즘을 도식화하여 Fig. 4에 나타내었다.

Fig. 4

Workflow for neural network training in the proposed method

3.3 예측 과정

훈련이 완료된 신경망 구조를 사용하여 학습에 사용되지 않은 파라미터의 q값을 수치계산 과정 없이 예측할 수 있다. 학습에 사용되지 않은 파라미터의 시간 구간과 Young’s modulus, 그리고 Poisson ratio로 X_k를 구성한다. 구성된 X_k를 input으로 활용하여 test data인 q_9∼12을 예측하는 $$ {\widehat{\mathbf{q}}}_{9~12}$$을 도출할 수 있다.

본 연구에서는 복원과정을 통해 도출된 $$ {\widehat{\mathbf{q}}}_{9~12}$$를 전체 변위 행렬인 U_9∼12로 복원한다. 먼저 학습에 사용되지 않은 예측값의 파라미터로 질량과 강성 행렬을 구성한다. 이 두 행렬을 iIRS method를 통해 예측값의 변환 행렬 T_9∼12를 구하고 이를 $$ {\widehat{\mathbf{q}}}_{9~12}$$에 곱하여 전체 변위 행렬인 $$ {\widehat{\mathbf{U}}}_{9~12}$$로 복원하게 된다.

이와 같은 방법으로 구해진 예측 결과 U_9∼12은 예측값의 파라미터로 구성된 input값을 신경망 구조에 입력하고 iIRS 변환 행렬을 구하는 것으로 큰 계산비용 없이 전체 변위 행렬을 구할 수 있다.

3.4 신경망 검증

제안된 방법은 감축된 q를 통해 학습이 이루어진다. 이번 섹션에서는 학습 데이터 q와 신경망을 통해 도출된 $$ \widehat{\mathbf{q}}$$을 사용하여 신경망의 정확도를 검증하였다.

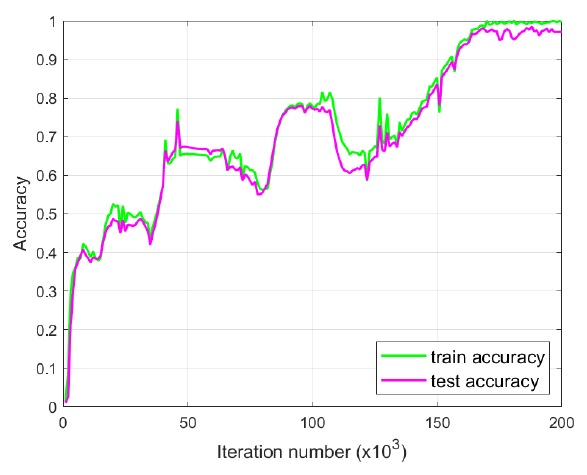
제안된 신경망의 q에 대한 예측필드 정확도는 Fig. 5에 나타내었다. Fig. 5에서는 training parameter ①~⑧을 사용한 신경망의 반복 횟수에 따른 training accuracy와 test accuracy를 나타내었다. Fig. 5의 train accuracy는 약 17만회 이후의 반복 횟수에서 q_1∼8의 99%에 근접한 유사도를 보였으며 test accuracy는 16~20만회의 반복 횟수 구간에서 약 5%이내의 오차를 유지하였다.

Fig. 5

Train and test accuracy of the trained neural network

다음 장에서는 수치 예제를 통해 기존의 전체 데이터를 학습하는 방법을 사용하여 구한 예측 데이터와 제시한 방법을 사용하여 도출한 데이터를 비교하여 검증하고자 한다.

4.1 모델 구성

기어 박스 하우징의 동역학적 거동은 샤프트 구동 시에 발생하는 홀 주변 외력에 의한 거동으로 가정할 수 있다. 이러한 동역학적 거동을 고려하면서 기어 박스 하우징을 경량화하기 위해서는 샤프트에 대한 동적 응답 특성을 파악하고 주요 부분에 대한 설계를 진행하여야 한다.

최근 전기자동차의 기어 박스 하우징은 기어 변속 과정이 생략되어 경량화 및 소형화의 가능성이 더욱 높아지게 되었다. 그러나 모터의 높은 토크에 의한 발진 시 초기 진동 및 회생 제동에 의한 진동으로 다양한 조건에서의 동적 응답 특성에 대한 계산이 필요하다.

이와 같은 조건에서 다변수 ROM-NN 구조는 대표적인 reference 데이터를 기반으로 반복적인 계산을 줄일 수 있는 방법이 될 수 있다.

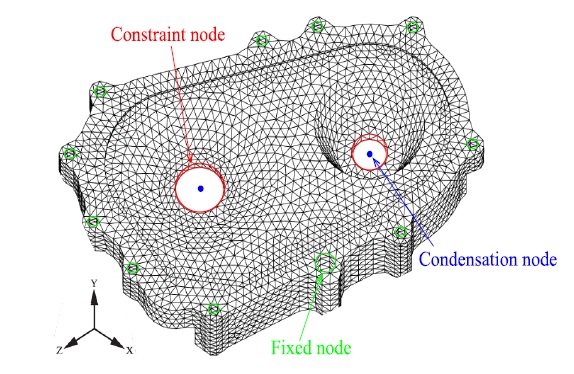
대상이 되는 기어 박스 하우징은 질량 및 강성 행렬에 다중점 구속 조건(multipoint constraints, MPCs)을 적용하여 샤프트가 연결되는 중심 부분 두 곳을 condensation node로 지정하고 외력을 가하는 방식으로 구성하였다^[12,13].

MPCs가 적용된 condensation node에서 받은 외력은 주변의 constraint node로 분산되어 하우징 전체에 힘이 전달된다. 즉, 샤프트에서 전달되는 외력은 condensation node 2곳을 통해 총 12개의 자유도로 함축되어 전달할 수 있어 식 (1)의 계산을 간편하게 만들 수 있다. 즉, 다중점 구속 조건을 사용하여 하우징 전체에 대한 정보를 함축하여 필요한 부분만을 계산하였다. Table 3에 하우징 모델의 파라미터들을 정리하였으며 Fig. 6에 변속기 하우징 모델의 형상과 주요 node 들의 위치를 표시하였다.

Table 3

Parameters of gearbox housing model

Fig. 6

Denotation for each type area at gearbox housing

4.2 변위 오차

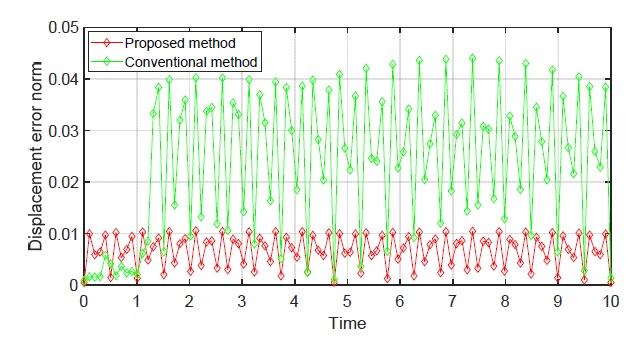
Fig. 6에서 제시한 기어 박스 하우징에 Table 3의 excitation forces에 대한 boundary condition을 설정하였고 이러한 조건 하에 기어 박스 모델의 외력에 의한 각 노드의 변위 변화량을 측정하는 것으로 앞에서 제시한 방법을 평가하였다. 해석 전체 시간 범위 구간을 0초부터 10초로 설정한 조건에서 제안된 모델과 기존 모델의 변위 오차 결과를 Fig. 7에 나타내었으며 표시된 변위 오차 결과는 각 노드 위치에 대한 전체 오차 값의 평균으로 도출하였다.

Fig. 7

Displacement error norm at entire time range

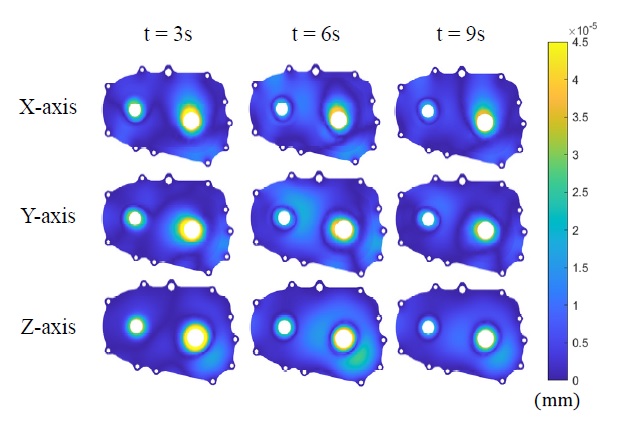
Fig. 7에서 기존의 NN 방법은 약 1.3초 이하의 시간 구간에서 높은 정확도를 보였지만 그 이후로는 제안된 ROM-NN 방법이 기존의 방법보다 더 낮은 오차를 보여주었다. Fig. 7의 결과에서 제시된 방법은 전체 모델의 평균적인 값에서는 오차가 낮을 수 있으나 모든 위치의 노드점에서 기존 모델보다 더 낮은 오차를 갖는다고 단정할 수 없다. 따라서 모델의 전체 노드점 위치에서 더 낮은 오차를 갖는지를 알기 위해 모델의 전체 노드점 위치의 변위 오차를 모두 구하여 평가하고자 하였다. 이를 시각적으로 표현하기 위해 contour를 활용하여 모델의 변위 오차 결과를 도식적으로 Fig. 8과 Fig. 9에 나타내었다. Fig. 8은 기존 NN 방법에서 x, y, z 각 방향을 기준으로 하는 변위 오차의 결과를 나타낸다.

Fig. 8

Displacement error of conventional method

Fig. 9

Displacement error of proposed method

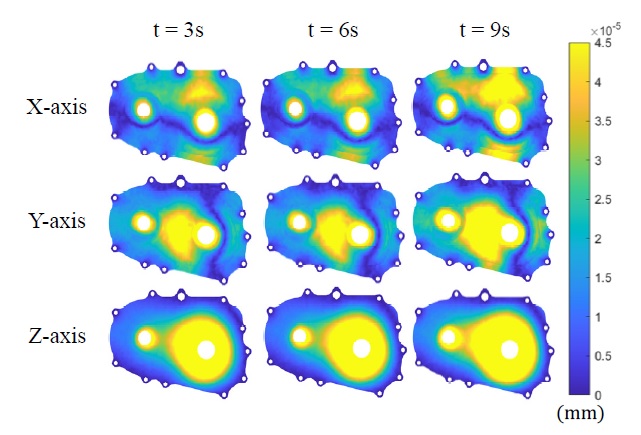
Fig. 9는 다변수 ROM-NN 방법을 사용한 변위 오차의 결과를 나타낸다. Fig. 8, 9에서 제시한 시간 간격 3, 6, 9초는 앞서 언급한 1.3초 이후의 결과를 동일한 간격에서 비교하기 위해 설정하였다.

Fig. 8과 비교해 Fig. 9는 표시한 3, 6, 9초 시간 간격에서 오차가 모두 감소하는 결과를 보였다. 모델에 외력이 직접적으로 작용하는 부분 외의 위치에서 오차가 확연히 감소하였고 x, y, z축의 모든 부분에서 더 낮은 오차를 나타내는 결과를 보였다.

이를 수치적으로 표현하기 위해 변위 행렬에 Frobenius norm 값을 계산하여 Table 4에 표시하였다. Table 4에 표시한 결과는 각 축에 대해 시간 구간의 평균값을 나타내었다. Table 4에서 제시한 다변수 ROM-NN 방법은 기존의 NN 방법에 비해 오차를 약 66% 감소시키는 것으로 나타났다. 이러한 결과로 제시된 방법은 기존의 NN 방법보다 약 300% 높은 정확도를 가지는 것으로 판단할 수 있다.

Table 4

Frobenius norm value of displacement error

4.3 von-Mises stress 결과 및 수렴성 비교

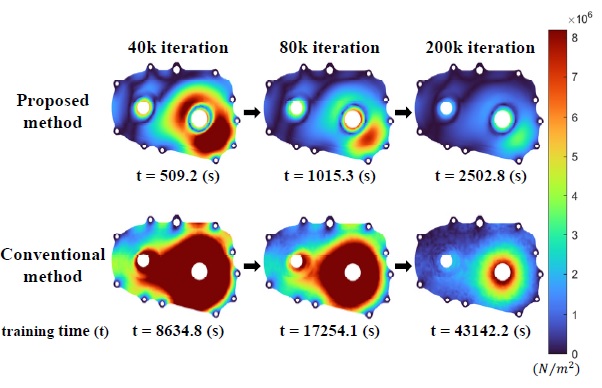
제시한 ROM-NN 방법을 응력에 대해서도 검증하기 위해 von-Mises stress에 대한 결과값을 Fig. 10에 나타내었다. Fig. 10에서 제시한 방법은 기존 NN 방법보다 같은 반복 횟수에서 더 낮은 오차를 보였다. 기존 NN 방법은 외력이 가해진 샤프트 홀을 중심으로 오차의 최댓값을 나타냈다. 이에 비해 제안된 방법은 기존 NN 방법과 비교해 수치적인 오차 감소뿐만 아니라 주요 부분인 샤프트 홀에서 오차의 최댓값을 갖지 않는 것을 확인할 수 있었다. Fig. 10에서는 하우징 모델의 수렴성을 비교하기 위해 각 모델의 학습 시간을 Fig. 10의 contour 아래에 각각 나타내었다. 학습 시간의 증가와 오차의 감소율을 보면 제안된 다변수 ROM-NN 방법이 기존의 NN 방법보다 수렴성이 더 높은 것으로 판단된다. 결과적으로, 제시한 다변수 ROM-NN 방법은 기존의 NN 방법의 약 94%가 감소된 계산 시간만을 필요로 하였으며 20만 번의 반복 횟수 내에서 기존의 NN 방법보다 더 높은 정확도를 보였다.

Fig. 10

von-Mises stress error and training time value